城市轨道交通列车运行自动调整的优化模型及算法研究

孙少军 王慧芳

（上海中铁通信信号国际工程有限公司，上海 200436）

1 概述

城市轨道交通具有运量大、速度快、安全便捷、可靠性高的特点，已经成为缓解城市交通压力的主要运输方式。正常运行情况下，列车是严格按照运行图来运行的。但是，城市轨道交通系统列车以随机汇集的城市居民及流动人口客流为运输对象[1]的这一特点，决定了城市轨道交通运输组织的复杂性，运行过程中必然会产生许多随机因素的干扰，导致列车的实际运行偏离计划运行图的情况发生。因此需要对列车的运行进行调整使其恢复按计划有序运行。尤其是基于通信的列车运行控制（CBTC）系统实现了移动闭塞技术，打破了传统的固定闭塞对于追踪间隔的限制，使得列车的追踪间隔明显减小，大大增加了行车密度，同时也增加了列车运行调整的难度。因此，对城市轨道交通系统中列车运行调整的研究是非常必要和重要的。

本文在参考国内外已有相关文献的基础上，结合城市轨道交通列车运行的特点，建立列车运行调整的优化模型，采用改进的遗传算法求解该模型，完成了列车自动调整的仿真测试。

2 列车运行自动调整模型

正常运行情况下，列车严格按照列车计划运行图运行，许多随机因素的干扰使得列车难免偏离计划运行图，造成行车紊乱。因此需要对列车的运行进行调整，使其尽可能恢复按计划有序运行。采用如下具有广泛意义的列车运行调整模型[2，3]。

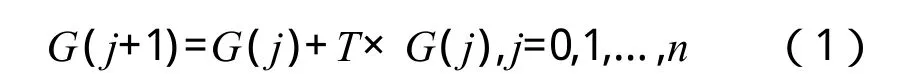
式中，G(j)为j时刻列车实际运行状态，T是由列车运行调整决策而决定的状态转移算子。

列车运行自动调整问题模型的建立主要分成两部分：一个是模型目标函数的确定；另一个是约束条件的确定。

2.1 目标函数

城市轨道交通列车运行自动调整问题实质就是根据线路上列车运行情况重新确定运行计划，使实际运行图不断逼近计划运行图，最终达到差异最小化的过程。运输部门在编制列车计划运行图时，已充分考虑了旅客平均等待时间、区间通过能力等因素，因此在重新确定运行计划时，只需考虑如何使得调整后的运行计划尽可能地接近原运行计划。在调整过程中需考虑以下两个因素。

1）列车总晚点时间

传统的城市轨道交通列车运行调整模型通常会将出发总晚点时间忽略，这对于采用移动闭塞方式的城市轨道交通系统列车运行调整的模型建立来说是很不严谨的。因为移动闭塞使得追踪列车之间没有固定的闭塞长度，后行列车的运行会受到前行列车运行状况的制约，前车的发车时间直接影响到后车的进站和离站时间。

这里的总晚点时间指的是列车运行到达总晚点和发车总晚点时间之和。

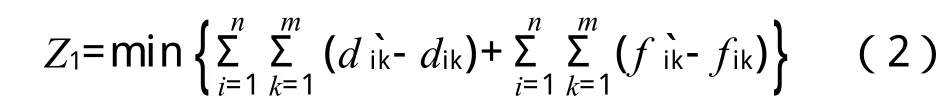
式中，n为列车总数，m为列车停站总数，dik和d｀ik分别为列车i在车站k的计划和实际到站时间，fik和f｀ik分别为列车i在车站k的计划和实际发车时间。

2）列车总晚点数目

同上，这里的总晚点数目指的是列车运行到达总晚点和发车总晚点列车数目之和。

式中，符号定义同公式（2）。

以列车总晚点时间和列车总晚点数目为综合优化目标，具体的优化目标Z可写成：

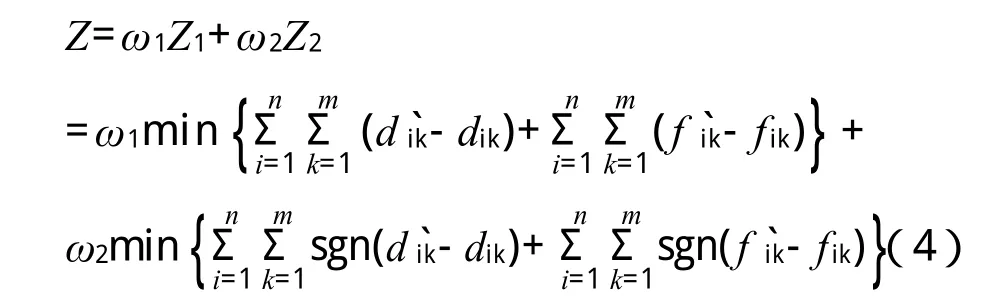
式中，ω1，ω2分别为Z1，Z2对应的权重因子。

2.2 约束条件

采用固定闭塞城市轨道交通系统的列车在运行调整时，主要考虑以下约束。

1）发车时间约束

列车实际发车时间不能早于计划发车时间。

即：列车实际发车时间不能早于计划发车时间。

2）最小停站时间约束

为了保证一定的载客量，规定了最小停站时间。列车实际停站时间不能小于本站最小停站时间。

式中，TkDmin是第k站最小停站时间。

3）区间运行时间约束

由于车辆的技术状态，线路限速等的影响，以及为了保证旅客的舒适度，必须保证一个最小的区间运行时间。

式中，TkTmin是第k站到k+1站的最小区间运行时间。

4）追踪间隔约束

为了保证行车的安全，列车的追踪间隔不能小于规定的列车追踪间隔。

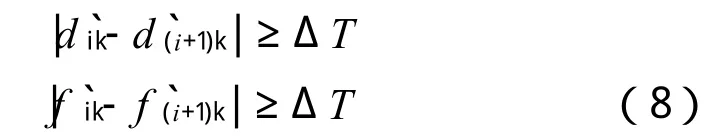
式中ΔT为列车的最小行车间隔。

3 模型求解

由上述分析可知，城市轨道交通列车运行调整问题是一个多目标、多约束的组合优化问题，是一个典型的NP问题。应用传统的分枝定界或逐步寻优方法进行求解时，在求解结果和收敛速度上都无法令人满意。随着智能技术的不断发展，特别是遗传算法成功解决了TSP、JobShop等组合优化问题以后，越来越多的学者把目光投向了它[3-5]，不过这些研究多是针对干线铁路或高速铁路的，真正针对移动闭塞下的城市轨道交通的运行调整的研究还非常少。本文采用改进的遗传算法来求解城市轨道交通中列车运行调整的问题。

3.1 染色体编码及种群初始化

列车运行调整问题实质上是重新确定列车时刻表的过程，变量均为列车的到发时间。采用整数编码的方式，对所有需要调整的列车到发时间进行编码。

以第一列列车当天开始运营从第一站的发站时间为零时刻，对时间偏移量以秒为单位进行整数编码。比如说第一列列车投入运营在首站的发车站时间为6:00:00，则6:00:30被编码为30。具体的染色体编码可以表示为：

n为列车总数，m为列车停站总数，dik表示到站时间，fik表示发站时间，m×n×2表示一条染色体上的基因总数，也即到发站时间数据的总个数。一条完整的染色体也就表示了在一段时间内的完整列车运行图。因为本文设计遗传算法求解的目的是得到预计的列车到发站时间，从而进行列车运行调整。

种群的初始化采用控制育种范围的初始化方式，根据调整计划相对于原计划的滞后性来控制育种边界，使初始化染色体对应位置的时间不小于原计划时间、不大于总晚点时间。

3.2 适应度函数的确定

适应度函数是对染色体适应环境能力的评价函数，一个染色体的适应度值越大，表明该染色体的适应环境的能力越强，即性能越好。本文建立的模型中的目标函数为最小化目标函数，因此需要进行变换。设计如下适应度函数：

由于所有约束条件均为硬约束，在计算适应度函数之前，需在遗传算法的实现中对7项约束进行检验，若有某项不满足，则该个体即遭淘汰，以此保证解的可行性。

3.3 种群演变策略

1）选择：按照个体在当前种群中的适应度值为繁殖概率进行个体选择。设种群中个体总数为C，则某一个体被选择的概率为：

2）交叉：使种群中不同的个体按一定概率Po进行染色体交叉。

3）变异：以概率Pm对染色体进行变异操作，即随机改变某个染色体的某一位值，以防止初始种群随机产生一些重要信息的缺失。

针对城市轨道交通列车运行调整的特点，为了加快收敛速度和获得有效的最优解，采用一些策略对遗传算法进行了改进。

*在遗传算法寻优过程中，初始化的染色体随机生成，收敛的速度很慢，难以达到列车运行计划实时调整的目的。如果初始化的染色体本身已经比较接近可行解，则经过交叉和变异，达到可行解的概率会大大增加。因此本文设计一种模式分类的方法，使得优化算法在初始化时，可以利用历史求解的结果作为初值，加快收敛速度。

*为防止找不到最优解的情况发生，本代中适应度最高的个体被保留，不经过染色体交叉直接复制到下一代，以避免破坏某些优良基因。

进行迭代寻优，当迭代次数达到最大迭代数后退出运算。选取适应度最高的个体作为最优解，即为调整后的运营计划。最大迭代次数的确定通过大量实验的方法来确定。

4 仿真验证

调整算法的仿真是在MATLAB7.0环境下应用英国谢菲尔德大学推出的遗传算法工具箱实现的。本文以北京地铁4号线为背景，进行列车运行调整的仿真实验。

选用从西单到中关村的12个站为调整区段，早8：00-9：00的时间为调整时间段。在线运行的列车数目为15。

列车在各区间对应的最小运行时间(单位：s)矩阵为：

TTmin=[150,150,150,150,150,150,90,120,120,90,120,120]

列车在各站对应的最小停站时间(单位：s)矩阵为：

TDmin=[40,40,40,40,30,30,40,30,40,40,40,40]

列车最小追踪间隔(单位：s)为：ΔT=150

经过多次的实验与分析，本实例中遗传算法的参数取：种群规模：100；遗传代数：50；交叉概率：0.6；变异概率：0.001。

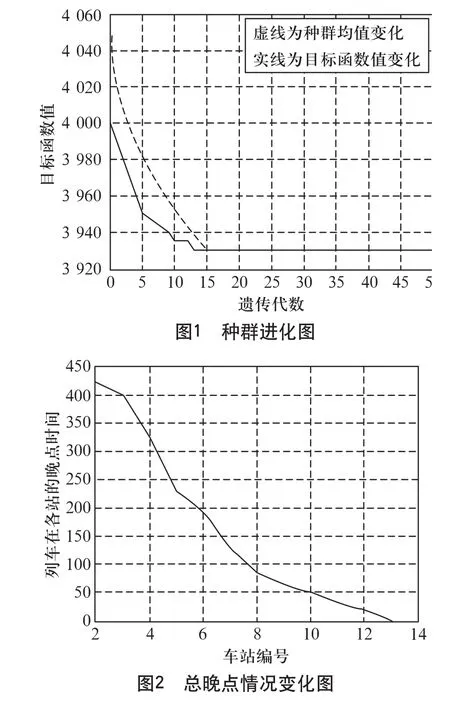
初始状态设为第6列列车在第2站晚点120 s。总晚点时间420 s。进行列车运行自动调整仿真分析。

从仿真结果可以明显看到，经过运行调整，随着到发时间线以及站序的推移，各站的总晚点时间不断减少，直至被消除从而恢复按计划运行图运行，如图1，2所示。从而证明，论文提出的优化模型的设计方案及求解算法对于城市轨道交通环境下列车的运行调整是有效性和可行的。

5 结论

本文通过分析采用移动闭塞技术的城市轨道交通列车运行的特点，建立了城市轨道交通列车的运行调整优化模型，并采用改进的遗传算法对该模型进行求解。以北京地铁4号线为背景进行仿真测试，模拟列车晚点情况，按本文所设计模型及求解方法进行自动运行调整。结果表明，本文建立的优化模型和采用的求解方法是合理的，可以满足列车正常运营自动调整的需求。

[1]吴洋．晚点情况下地铁列车实时运行调整及速度控制模式研究[D]．成都：西南交通大学，2004.

[2]张亦南．基于GA的列车自动调整算法在CBTC系统中的应用研究[D]．北京：北京交通大学，2018.

[3]李平，贾利民．遗传算法在列车运行调整中的应用研究[C].2001年中国智能自动化会议论文集，2001.

[4]章优仕，金炜东．基于遗传算法的单线列车运行调整体系[J].西南交通大学学报，2005,40(2):147-152.

[5]张文修，粱怡．遗传算法的数学基础[M].西安：西安交通大学出版社，1999.

[6]郭廓．现代有轨电车中央行车指挥系统研究[D]．北京：北京交通大学．2011.