重载铁路曲线几何参数对钢轨磨耗影响的研究
2013-05-04马战国司道林
李 伟,马战国,司道林
(中国铁道科学研究院铁道建筑研究所,北京 100081)
随着货运密度和轴重的不断提高,小半径曲线外股钢轨侧磨速率明显加快,曲线内轨压溃严重,轨面出现波磨,降低了运输效率,并增加了行车安全隐患。
曲线钢轨磨耗和机车车辆的车轮磨耗研究,已取得了一些突破性的成果[1-2]。为了降低小半径曲线钢轨磨耗的速率,延长钢轨的使用寿命,采取了提高钢轨强度等级、改善轮轨润滑条件、改善机车车辆转向架转向性能[3]、改变车轮踏面形状、钢轨预防性打磨以及改变轨道结构几何参数设置等措施。
我国现有货车最大轴重为25 t,而美国、巴西、加拿大及澳大利亚等国的货车轴重均不低于30 t,而且正积极发展40 t轴重货运技术。在上述多项养修措施中,合理设置曲线几何参数,不仅成本低,而且易于实现。我国正处于发展大轴重货运技术之际,积极研究小半径曲线钢轨轨底坡和超高[4]的取值,对改善小半径曲线区段的轮轨动力作用具有重要意义。
本文以曲线几何参数超高和轨底坡为分析重点,对半径分别为500 m,600 m,800 m 3种半径下的钢轨磨耗指数、轮轨力、轮对冲角等曲线通过性能指标进行分析,同时在现场设置试验段,并提出合理的曲线几何参数设置值。
1 动力学仿真计算模型
1.1 车辆模型
本文采用多体动力学分析软件NUCARS,建立了我国25 t轴重货车动力学模型。我国25 t轴重货车主型转向架为K6,该转向架为三大件式系铸钢货车转向架。一系悬挂采用轴箱弹性剪切垫;二系悬挂采用带变摩擦减振装置的中央枕簧悬挂系统,摇枕弹簧为二级刚度;两侧架之间加装侧架弹性下交叉支撑装置;采用直径为375 mm的下心盘,下心盘内设有含油尼龙心盘磨耗盘;采用JC型双作用常接触弹性旁承;安装25 t轴重双列圆锥滚子轴承。
通过长期理论和试验验证NUCARS软件在货车摩擦副建模方面取得了明显优势,可较为准确地模拟三件货车转向架摩擦减振特性。为使计算更为合理,建模时全面考虑了系统自由度和非线性环节。在摇枕和车体之间的心盘连接考虑成一个回转摩擦副;侧架和摇枕间考虑了摇枕弹簧的垂向、横向和纵向刚度,摩擦楔块考虑成双向摩擦副,轴箱悬挂纵向和横向用弹簧阻尼单元来模拟,竖向由两个摩擦副来模拟。车辆模型如图1所示。

图1 车辆模型
根据转向架各部分的运动特点及多体动力学理论[5],合理定义刚体数量及其自由度。模型由左右侧架、一个摇枕、两个轮对组成;摇枕考虑横移、沉浮、侧滚、摇头4个自由度,侧架考虑纵向、横移、沉浮、点头、摇头5个自由度,轮对考虑横移、沉浮、侧滚、摇头4个自由度。因此,完整的车辆模型共有49个自由度,如表1所列。

表1 车辆模型自由度
1.2 轨道模型
轨道模型由钢轨、扣件、轨枕和道床组成。钢轨、轨枕视为弹性点支承的欧拉—伯努里梁,扣件等效为并联刚度—阻尼系统。根据实测数据将道床换算为轨枕支承刚度和阻尼。采用模态叠加原理计算钢轨位移和加速度。
NUCARS轨道模型由若干个轨道单元组成。为使轨道模型不受边界条件的影响,建立的轨道单元模型长度为50 m,包含84个轨枕。分别计算75 kg/m钢轨、Ⅲ型轨枕的模态振型,截止频率分别为60 Hz和20 Hz,此外轨枕具有垂向和侧滚自由度,以此反应左右侧轨道不同的支承状态。扣件间距为0.6 m,扣件刚度为90 kN/mm。轨枕与基础间等效为八组并联弹簧阻尼联结,并联后的刚度与轨枕支承刚度120 kN/mm相当。阻尼定义刚度的0.25倍。模型结构如图2所示。

图2 轨道模型
2 模型验证
为验证上述模型的合理性,将仿真计算结果与试验测试数据进行了对比。采用实测轨道不平顺数据作为系统激扰,以计算模型的动力响应。图3给出了4项实测轨道不平顺样本。

图3 实测轨道不平顺样本
图4给出了试验车通过曲线时轮轨相互作用力响应、脱轨系数的试验结果与理论仿真计算结果。由图4(a),图4(b)可以看出,试验测量的内侧轮轨横向力最大值为35 kN,仿真计算的内侧轮轨横向力最大值为36 kN,试验测量的外侧轮轨横向力最大值为65 kN,仿真计算的外侧轮轨横向力最大值为54 kN。由图4(c),图4(d)可以看出,试验测量的内侧脱轨系数0.34,仿真计算的内侧脱轨系数0.37,试验测量的外侧脱轨系数0.51,仿真计算的外轨脱轨系数0.55;总体而言,仿真计算的响应波形与试验测量的响应趋势颇为一致。
通过试验值与理论值的对比可知,所建立的模型是合理的。这为以下的动力学分析提供了理论依据。
3 曲线几何参数设置对钢轨磨耗的影响
3.1 曲线超高对钢轨磨耗的影响
车辆通过曲线时,导向轮的动力学指标明显大于拖轮,对轨道的动力作用也最为显著。为分析曲线超高对钢轨磨耗的影响,设置不同的超高值,分析车辆曲线通过时导向轮对的轮对冲角、外轨横向力以及磨耗指数的变化规律。采用超高变化率(实设超高与均衡超高之差值占均衡超高的百分比)来描述超高的变化幅值,分析中超高变化率变化范围为 -20% ~20%(负值为欠超高、正值为过超高)。
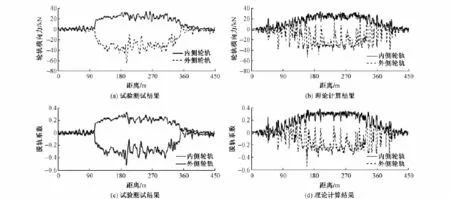
图4 试验值与理论计算结果对比
图5为C70型货车以时速75 km通过半径500 m,600 m,800 m三种曲线时的动力学响应。由图5(a)可以看出,随着曲线超高的不断增大,三种工况下的导向轮轮对冲角均不断增大。当超高变化率由-20%增至20%时,车辆通过半径500 m曲线时的轮对冲角由5.114 mrad增至5.613 mrad,增加了9.8%,车辆通过半径600 m曲线时的轮对冲角由4.451 mrad增至4.968 mrad,增加了11.6%,车辆通过半径800 m曲线时的轮对冲角由3.931 mrad增至4.161 mrad,增加了5.9%,因此,车辆通过半径500 m和半径600 m小半径曲线时的冲角增幅明显大于半径800 m曲线。此外,相同超高变化率条件下,曲线半径越大,轮对冲角越小;以超高变化率 -20%为例,对应于3种半径下的轮对冲角分别为 5.114 mrad、4.451 mrad和3.931 mrad,半径为600 m曲线较半径为500 m曲线减小幅值为13.0%,半径800 m曲线较半径为600 m曲线减小幅值为11.7%。
图5(b)为外轨横向力与超高变化率的对应关系。可以看出,随着曲线超高的不断增大,3种曲线半径工况下的外轨横向力均不断减小。当超高变化率由-20%增至20%时,车辆通过半径500 m曲线时的外轨横向力由 26.494 kN增至 25.269 kN,减幅为4.6%,车辆通过半径600 m曲线时的外轨横向力由26.156 kN增至25.202 kN,减幅为3.6%,车辆通过半径800 m曲线时的外轨横向力由24.761 kN增至23.953 kN,减幅为3.3%。可见,外轨横向力受轮对冲角和离心力的综合作用,减幅很小。相同超高变化率条件下,曲线半径由500 m增至600 m后,外轨横向力减幅很小,而曲线半径由600 m增至800 m后,外轨横向力减幅较大。

图5 超高对磨耗指标的影响规律
图5(c)为磨耗指数与超高变化率的对应关系。随着曲线超高变化率的不断增大,3种曲线半径R工况下的磨耗指数均不断减小。当超高变化率由-20%增至20%时,车辆通过半径500 m曲线时的磨耗指数由 111.042 kN·mrad增至107.187 kN·mrad,减幅为3.5%,车辆通过半径600 m曲线时的磨耗指数由 92.088 kN·mrad增至 87.894 kN·mrad,减幅为4.6%,车辆通过半径800 m曲线时的磨耗指数由66.085 kN·mrad增至63.506 kN·mrad,减幅为 3.9%。与上述两项指标不同的是,相同超高变化率条件下,随着曲线半径的增大,磨耗指数明显降低;例如,当超高变化率为-20%时,对应于3种半径下的磨耗指数分别为111.042,92.088,66.085 kN·mrad,半径为 600 m曲线较半径为500 m曲线减小幅值为17.1%,半径为800 m曲线较半径为600 m曲线减小幅值为28.2%。
曲线区段设置一定的欠超高时,由于离心力的作用,增大了轮对横移量,从而导致内外轨的滚动圆半径差增大,有利于轮对趋于径向位置,减小了轮对冲角。此外,适当欠超高值增大了拖轮的导向作用,从而减小了导向轮的导向力。
结合以上3项动力学指标,设置适当曲线欠超高可减小轮对冲角和磨耗指数,然而受外轨横向力的限制,曲线欠超高值宜取在10% ~20%之间,这与文献[2]中的结论相符。此超高设置范围也在轨底坡取值分析中得到采用。
3.2 轨底坡对钢轨磨耗的影响
采用上节中的评价指标,分析轨底坡对车辆曲线通过性能影响规律,轨底坡的设置共有以下4种方案:方案1为内股钢轨轨底坡1/40、外股钢轨轨底坡1/40;方案2为内股钢轨轨底坡1/20、外股钢轨轨底坡1/20;方案3为内股钢轨轨底坡1/40、外股钢轨轨底坡1/20;方案4为内股钢轨轨底坡1/20、外股钢轨轨底坡1/40。
采用上述轨底坡设置方案,对比分析4种方案下C70货车以时速70 km通过半径为500 m,600 m,800 m 3种曲线时的动力学响应。分析时采用的曲线超高变化率为-15%。
图6可以看出不同轨底坡设置方案对导向轮冲角、外轨横向力和磨耗指数的影响规律。由图中曲线不难发现,4种轨底坡方案对应的动力学指标表现出明显的非线性变化。车辆通过3种半径R曲线时,方案4对应的动力学指标最小,方案2次之。

图6 轨底坡设置对磨耗指标的影响规律
我国现有曲线区段轨底坡设置为方案1,采用方案4后,车辆通过半径为500 m,600 m,800 m曲线时的动力学均有所改善,3种半径曲线对应的轮对冲角分别由 5.187 mrad,4.596 mrad,3.985 mrad 减小至5.127 mrad,4.375 mrad,3.470 mrad;三种半径曲线对应的外轨横向力分别由26.317 kN,25.938 kN,24.532 kN减至24.866 kN,22.950 kN,20.608 kN;3种半径曲线对应的磨耗指数分别由108.692 kN·mrad,89.376 kN·mrad,63.855kN·mrad 减 至 103.83kN·mrad,80.968 kN·mrad,56.488 kN·mrad。
究其原因,外轨采用1/40的轨底坡,轮轨接触点移向轮缘根部,内轨采用1/20轨底坡,轮轨接触点远离轮缘根部,由于车轮踏面的锥度影响,使得曲线外侧轮轨接触滚动圆半径增大,曲线内侧轮轨接触滚动圆半径减小,增大了内外侧的滚动圆接触半径差,改善了车辆的曲线通过性能。此外,文献[2]对曲线内外轨非对称轨底坡对钢轨的磨耗进行了研究,认为将轨底坡由1/40改为1/20可在一定程度上改善轮轨接触状态,提高车辆的曲线通过性能。
通常我国在轨枕承轨台设置1/40坡度来实现轨底坡的设置,为改变轨底坡设置带来了一定难度。
4 曲线磨耗现场测试
在上述理论分析的基础上,分别设置轨底坡和曲线超高的现场试验段,对钢轨侧磨量进行定期观测;分析轨底坡和曲线超高对钢轨磨耗的影响规律。表2列出了试验段曲线设置参数,共设置了3个试验段。
对试验段的钢轨设置测量点,测量点的间距为10 m,测量周期为1个月。曲线钢轨磨耗具有显著的不均性,圆曲线区段钢轨磨耗最为明显,因此以圆曲线内的钢轨侧磨平均值为指标与历史数据进行对比。表3~表5分别列出了试验段内钢轨的历史和试验磨耗数据。
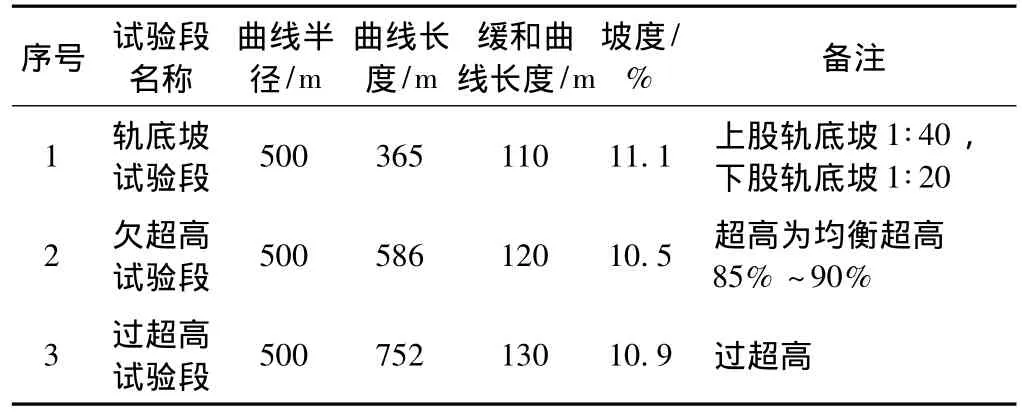
表2 试验段曲线设置参数
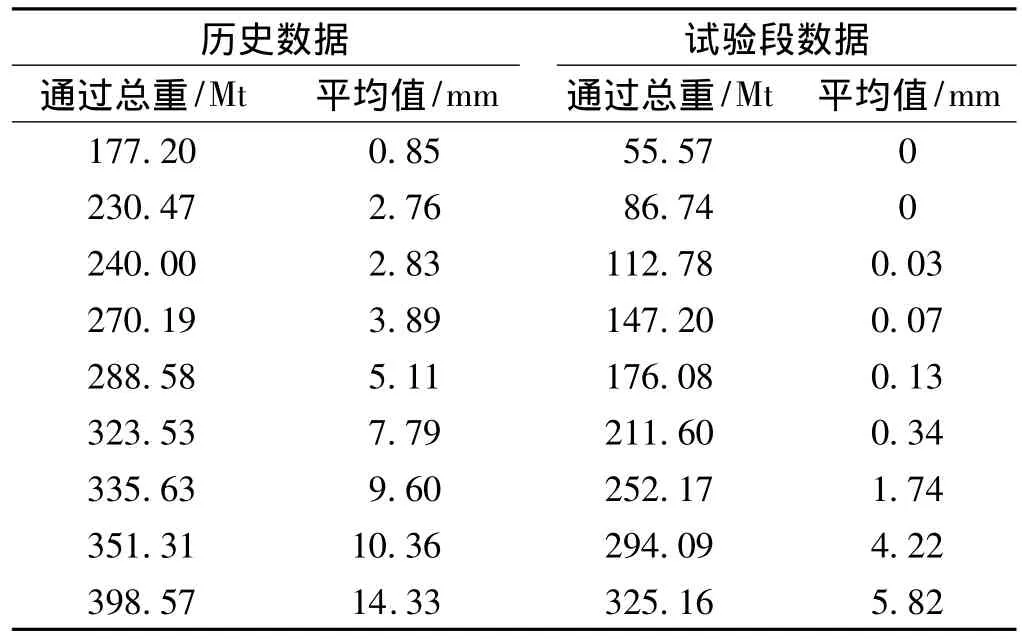
表3 轨底坡试验段钢轨侧磨测量数据

表4 欠超高试验段钢轨侧磨测量数据
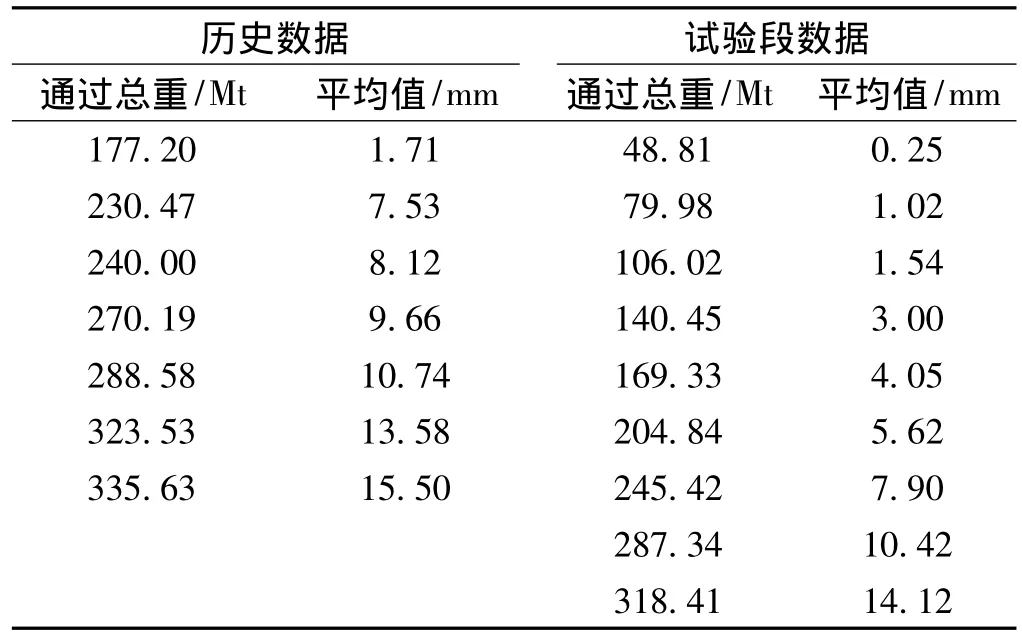
表5 过超高试验段钢轨侧磨测量数据
由表3可以看出,轨底坡试验段圆曲线范围钢轨侧磨值明显减小,通过总重为325.16 Mt时,既有钢轨侧磨平均值为7.79 mm,试验段钢轨侧磨平均值为5.82 mm,与既有圆曲线钢轨侧磨平均值相比,试验段钢轨侧磨平均值降低了约25.16%。
由表4可以看出,欠超高试验段圆曲线范围钢轨侧磨值可明显减小,通过总重为323.47 Mt时,既有钢轨侧磨平均值为9.32 mm,试验段钢轨侧磨平均值为7.82 mm,与既有圆曲线钢轨侧磨平均值相比,试验段钢轨侧磨平均值降低了约16.09%。
由表5可以看出,过超高试验段测量数据,圆曲线范围钢轨侧磨值与既有钢轨基本一致。通过总重为318.41 Mt时,既有钢轨侧磨平均值为13.58 mm,试验段钢轨侧磨平均值为14.12 mm。
由试验结果分析可知,曲线区段欠超高和非对称轨底坡的设置均在一定程度上减轻了外股钢轨侧磨,同时也验证了理论仿真分析的结果。
5 结论
1)磨耗指数为轮对冲角和横向力的综合反映。现场调查时发现,随着曲线半径的增大,尤其当曲线半径>800 m后,钢轨磨耗速率明显下降。
2)设置适当曲线欠超高可减小轮对冲角和磨耗指数,然而受外轨横向力的限制,曲线欠超高值宜取在10% ~20%之间。
3)曲线内外轨非对称轨底坡(内轨1/20、外轨1/40)的设置可改变轮轨几何接触状态,在一定程度上提高了车辆通过曲线的性能。
4)轨道几何参数对3种小半径曲线车辆动力学指标的影响规律一致,为减小曲线钢轨磨耗速率,可采用相同的轨道几何参数。
曲线区段欠超高和非对称轨底坡的设置均在一定程度上改变了轮轨接触状态,所不同的是,曲线欠超高未改变轮轨接触几何参数,而轨底坡的设置改变了轮轨接触几何参数。分析现场试验段的观测数据,两种措施均在一定程度上减小了钢轨磨耗,这为今后综合试验措施的实施奠定了基础。
[1]练松良,孙琦,王午生.铁路曲线钢轨磨耗及其减缓措施[M].北京:中国铁道出版社,2001.
[2]卢家方,张通,孙琦,等.在内燃牵引下减缓曲线钢轨侧面磨耗的研究[J].中国铁道科学,1990,11(2):74-91.
[3]李亨利.货车径向转向架动力学特性及轮轨磨耗研究[D].成都:西南交通大学,2006.
[4]魏稚仑,何大芳,张元栋.轮轨关系中轨底坡与曲线超高的新评价[J].铁道工程学报,1987(2):217-223.
[5]翟婉明.车辆—轨道耦合动力学[M].3版.北京:科学出版社,2007.
