地下连续墙钢筋笼滑吊骨架承载力验算

2013-05-04杨天鸿

铁道建筑 2013年6期

杨天鸿

(中国铁建十二局集团第二工程有限公司，山西太原 030032)

1 工程概况

长沙地铁五一广场站位于长沙市五一大道与黄兴中路道路交叉口下，地铁2号线与1号线呈“十”字形岛式换乘。2号线主站体顺五一大道东西向布置，1号线主站体顺黄兴中路南北向布置。2号线主站体围护结构采用1 000 mm厚地下连续墙，连续墙深31.5 m，共72槽段，单幅连续墙钢筋笼质量约36 t;1号线主站体围护结构采用800 mm厚地下连续墙，连续墙深22.23 m，共132槽段，单幅连续墙钢筋笼质量约30 t;明挖区间段围护结构采用1 000 mm厚地下连续墙，连续墙深约37 m，共39槽段，单幅连续墙钢筋笼质量约42 t，钢筋笼最长达42.89 m。除了标准的方形笼以外，还有转角部位的异形笼如T形笼、Z形笼、L形笼等，以及车站端头部位使用玻璃纤维筋的大宽度钢筋笼。实际施工中，30 m以上钢筋笼全部采用单台吊车起吊。

连续墙钢筋笼从制作、起吊直至放置到位所耗费的成本占连续墙成本的一半以上，且安全风险大。目前施工单位的钢筋笼吊装方案中验算的内容主要为吊具、吊点与吊车;而在钢筋笼吊装的施工现场，起吊失败的原因几乎都是钢筋笼骨架失稳。以长沙地铁五一广场站为例，因为场地有限的关系大部分钢筋笼采用单台吊车起吊，虽然未出现严重事故，但是起吊钢筋笼时桁架筋的局部破坏频繁发生。为了满足连续墙施工中钢筋笼吊装更安全、更快速且占地更小的实际要求，施工人员必须掌握单台吊车起吊钢筋笼时，其骨架在起吊过程中受力的变化及其验算方法。

2 钢筋笼起吊的受力规律与破坏形式

五一广场站钢筋笼单台吊车起吊时，主钩吊绳悬挂铁扁担，钢丝绳穿过铁扁担上的五个滑轮分别连接在钢筋笼顶部和中部吊点上，多组葫芦同时工作，使钢筋笼的起吊角度逐渐趋向垂直，最终竖直提起，见图1。起吊过程中是以钢筋笼中桁架筋作为受力单元，每榀桁架由上下部主筋和W形腹筋(以下称W筋)形成，多榀桁架之间通过剪刀筋相连接形成一个整体受力的吊装骨架。纵向钢筋和水平钢筋通过梅花电焊形成网片连接在骨架上。当钢筋笼骨架受力时由W筋承受剪力，并由上下网片辅助桁架上主筋承受弯矩与轴力。

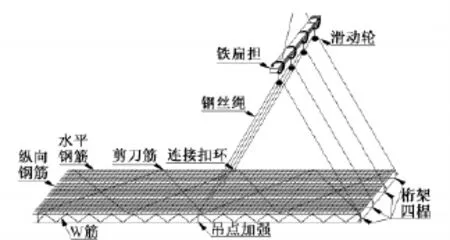
图1 钢筋笼单台吊车起吊

2.1 吊起过程中吊绳力与地面反力的变化

钢筋笼从水平平躺到竖立悬吊的过程中，随钢筋笼体与地面夹角即起吊角度的变化，地面反力的变化存在极值。从钢筋笼微微抬起到旋转到大约70°角之前，地面反力增大;在达到峰值后，地面反力迅速减小直至钢筋笼吊离地面。滑轮上吊绳的受力规律正好相反，先减小后急剧增大。

2.2 滑吊中钢筋笼弯矩分布

钢筋笼起吊过程中，由于滑轮的摩擦阻力很小，滑轮两端吊绳力可以认为相同，与竖直向夹角亦相同。一台吊机单排滑轮起吊过程中弯矩分布图为双峰形式，钢筋笼全范围为正弯矩，即下层钢筋受拉。

3 计算模型

3.1 受力分析

钢筋笼只承受三种力即地面反力Fd，吊绳力F和自身重力Qg，在同一平面内没有多余约束，属于静定问题。其中Fd的方向始终朝上，Qg的方向则始终朝下，F的方向随钢筋笼起吊角度的变化而变化(见图2)。由于滑轮的摩擦阻力很小，可以假定滑轮两侧吊绳的力都为F。假设不存在地面摩擦力和风力，只有地面力、吊绳力和钢筋笼重力，三者平衡。可以列出竖向力平衡方程，求解外力后即可计算钢筋笼承受的弯矩。

3.2 几何分析

由于滑轮起吊的特殊性，滑轮能在钢绳上自由滑动，当钢筋笼抬起角度α变化时，吊绳与钢筋笼之间夹角也同时变化，这是钢筋笼受力计算中的难点。通过分析发现，假定吊绳长度不变，起吊过程中铁扁担上滑轮中心的轨迹是椭圆，如图3。钢筋笼吊装过程中起吊角度θ和和吊绳夹角α之间的几何关系式(L/2+X)cosα =Lssinθ

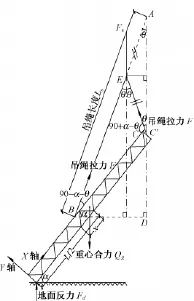
图2 钢筋笼吊绳夹角与起吊角关系示意

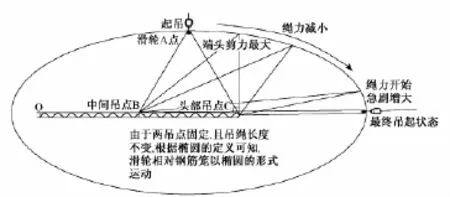
图3 钢筋笼起吊过程

3.3 编程计算

如果采用MATLAB编程的方式求解钢筋笼内力及外力，则有以下流程，如图4。根据现场情况将设计图纸的参数代入程序。

图4 计算流程示意

4 工程实例分析

以五一广场站连续墙的二期钢筋笼为例，其C型墙二期钢筋笼长为30.3 m，宽6 m，W筋角度为设计45°，桁架有5榀，吊点设在重心位置，距离中心向下2 m。钢筋笼桁架高度1.02 m，吊绳长度34 m。通过现场吊车测量，钢筋笼吊起时的质量为40.3 t，吊具(铁扁担、吊绳、扣环)质量为8 t。

得到 L=30.3 m，m=38 t，X=2 m，h=1.02 m，Ls=34 m，假设钢筋笼质量平均分布，吊车吊绳始终保持垂直，钢筋笼与地面之间没有摩擦力作用。将已有参数代入公式，进行编程计算后可以得到如下结果。

4.1 吊绳力F和地面反力Fd

地面反力Fd随钢筋笼吊立角度而变化，地面反力开始为115 kN左右，随吊起角度变大而增大，达到最大值158 kN后，迅速减小直至被提起。钢丝绳上的拉力则正好相反，随钢筋笼起吊而逐渐减小，在弧度为1.318即角度70°时，吊绳力最小达到112.8 kN，之后吊绳力急剧增大，进入吊起状态。将计算得到的地面反力最大值与实际的地面反力最大值比较，分别为158 kN与203 kN，偏差的主要原因为起吊过程中由于吊车司机操作原因，铁扁担上方吊绳未能在吊车推移过程中始终保持垂直。

4.2 钢筋受压力max(M/h+N)，N1，N2

钢筋笼底部W筋轴力N1在起吊后一定角度达到最大值，本例中在弧度0.47即角度27°时，达到最大值178.4 kN，上部W筋轴力N2在弧度0.272 6即角度15.6°时，达到最大值197 kN。桁架受力主筋沿长度方向的最大轴力max(M/h+N)在弧度0.424即角度24.3°时，达到最大值875.1 kN。再将该角度代入原公式，可知破坏位置在中点向上3 m，即最大弯矩处。

4.3 最大弯矩Mmax

当起吊角约为0时，在距离笼底19.9 m的位置有最大弯矩667.5 kN·m。

4.4 骨架参数选定

4.4.1 桁架W筋剪力承载力的验算

由于二期槽钢筋笼设计W筋为φ20钢筋，无法满足单台吊车吊装要求，经抗剪承载力验算，确定选用φ25钢筋作为W筋。W筋与主筋夹角为50.43°，并对两端端头增加W筋进行加固，角度加固范围为上下端各6 m，加固钢筋采用φ25。

效益分析:二期钢筋笼共增加钢筋用量0.626 t，远远小于增加一台吊车所需要的租赁费用，且减少了场地占用，增加了连续墙强度，简化了吊装程序。

4.4.2 桁架主筋弯矩承载力验算

桁架承受弯矩时可以将轴力传递到覆盖在桁架筋上的钢筋网片上，确定钢筋笼上主筋帮助桁架上主筋受力的增益系数γ是该承载力验算的关键。其中γ的意义在于:N合×γ+N桁架=N合，通过ABAQUS软件建立有限元模型。首先，只放入水平钢筋和纵向钢筋，经过计算得到，唯有中间三排桁架上相邻两根纵向钢筋上的应力是桁架上主筋的0.1倍，其它纵筋上的应力是桁架主筋的0.01倍，故除中间三根桁架上主筋和各自相邻的两根纵向钢筋以外的应力都可忽略不计，可得到γ=合力/5×(3×2×0.1)/合力=0.12。

然后放入剪刀筋、水平钢筋和纵向钢筋，同一截面内，计算得到的剪刀筋上的应力是桁架上主筋的0.25倍，与剪刀筋相交的桁架主筋以外其他钢筋的应力是桁架上主筋的0.1倍，共6根，其他可忽略不计。可得到γ=合力/5×(0.25/1.414×2+6×0.1)/合力=0.19。可以作如下假设:钢筋笼起吊计算时，焊接良好的剪刀筋可以等效为与受力主筋共同承受弯矩产生的轴力。经验算后，满足吊装要求。