基于矢量夹角的改进型编码基因落点定位
2013-05-04官章健王雪梅陈昊明沈方泉
官章健,王雪梅,陈昊明,沈方泉
(1.第二炮兵工程大学,陕西 西安 710025;2.第二炮兵装备研究院三所,北京 100085)
0 引言
弹道导弹子母弹落点精度是评定其对目标毁伤效果的重要条件。在文献[1]中已经对多弹头落点激波定位的算法进行研究,其仿真结果表明,通过探测弹丸因超音速飞行所形成的激波进行定位具有很好的定位效果。但该算法需要根据下落弹头数来调整敏感系数的大小,若敏感系数不合适则很容易产生虚假定位点或丢失真实落点,甚至使程序进入死循环状态,造成定位结果的不准确,从而给子母弹的毁伤效果评估带来影响。针对以上不足,本文提出基于同一弹道线上4点决定的各矢量之间的夹角关系的改进型编码基因多弹头落点激波定位算法。
1 多弹头落点定位算法
1.1 单弹头落点定位原理
在导弹落点的测量区域内布置4个正四面体传感器阵列(如图1)敏感弹丸因超音速飞行而产生的激波信号[2],再利用得到的激波信号时间差算出各传感器阵列的波达方向向量LA,LB,LC,LD[3]。设置四个阵列中心点均在同一水平面上,以阵列A中心点为原点建立空间直角坐标系OAXYZ,利用文献[3]DOA模型估计弹丸弹道轨迹的方法,则图1中向量LA,LB,LC,LD满足方程组[3]:
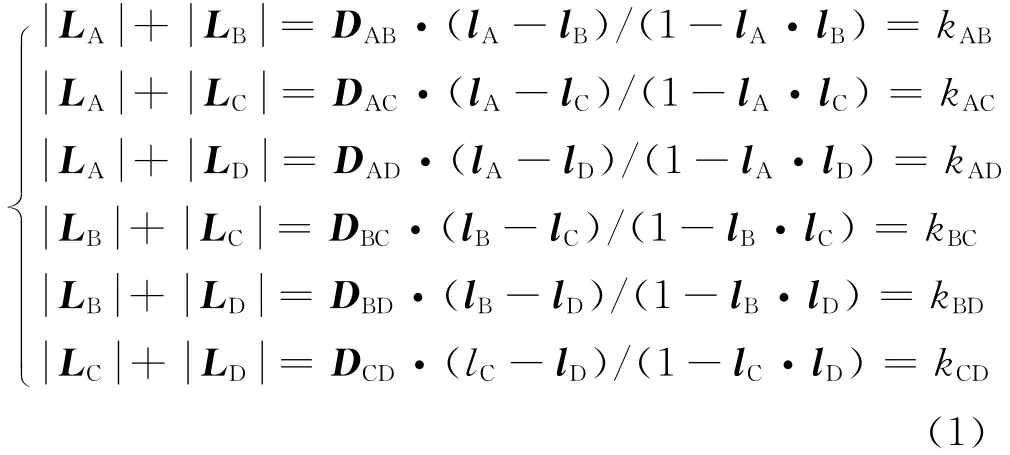
式(1)中,LI为I(I=A,B,C,D)阵列的波达方向向量,lI为相应的单位向量。DIJ为阵列I、J(J=A,B,C,D)之间的位置矢量。kAB,kAC,kAD,kBC,kBD,kCD表示下标代表的阵列计算的波达方向向量模长的和。通过计算求解|LA|,|LB|,|LC|,|LD|并采用最小二乘法得出弹丸下落弹道的空间轨迹方程。最后利用z轴坐标值计算得出弹丸的落点。
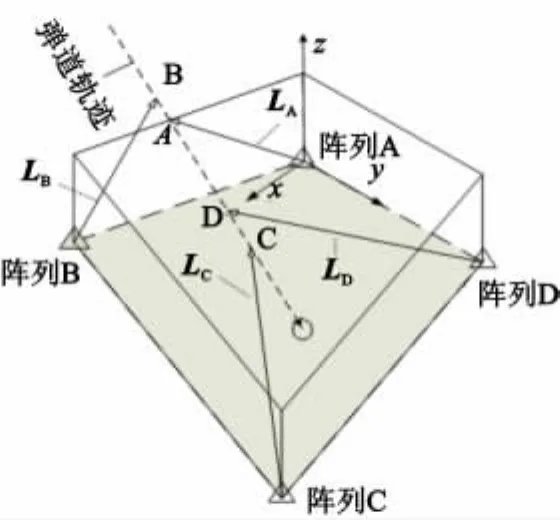
图1 波达方向确定弹头轨迹原理Fig.1 Direction of shock wave to determinate trajectory
1.2 编码基因[1]概念
编码基因:将各阵列所计算出的波达向量进行编号,确定波达向量在矩阵中位置,利用产生的随机数字来代表相应阵列的波达向量,取出每一阵列的一个数组合成列向量,即为一个编码基因。
例如:定位5个弹头时,给每个弹头分别设置编号1、2、3、4、5,每个阵列能计算产生5个波达方向向量。以A阵列为例,按照其接收到的各弹头激波信号的时间顺序计算得到的向量分别为l2A1,l3A2,l4A3,l1A4,l5A5。上标表示产生该波达向量的弹头号,按上标数字从小到大排序后再将下标数字按顺序组成一个行向量[4 1 3 2 5]。同理产生阵列B、C、D的行向量。最后所有行向量按行排列成矩阵(2):
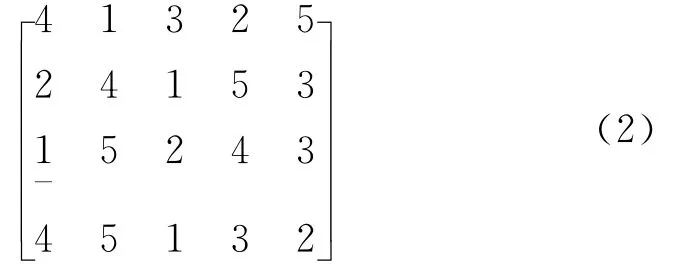
带下划线的元素1意义为:在第3个(行数)传感器阵列(C阵列)敏感得到第1个(元素值)波达向量是由1号(列数)弹头的激波触发的。其中矩阵的每个列向量为一个编码基因,每个编码基因代表的是一个弹头轨迹上产生的波达向量。
1.3 编码基因多弹头落点激波定位算法[1]
假设定位5个弹头时,系统随机产生一个4维的列向量即“搜索基因”,列向量的每个元素在1~5之间。
利用最小二乘算法求解方程组(1),按公式(3)定义搜索基因的误差,若搜索基因相对应的波达向量属于同一弹道,则最小二乘解的误差将很小,反之误差可能非常大。
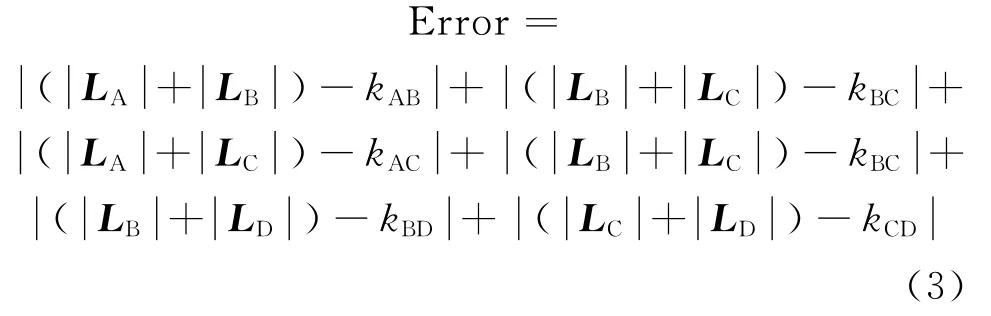
同时,设定敏感系数Sensitivity,当满足Error<Sensitivity时,将此相应的“搜索基因”保存为“优良基因”。仿真经验表明,敏感系数的设定应使搜索出的优良基因个数为实际弹头数目的2倍以上,否则真实的落点信息将会丢失。若敏感系数太大会加大下一步基因筛选的难度。敏感系数的设定最好能使优良基因的个数在实际弹头数的2~3倍之间。
根据弹头的数目设置循环次数Repetition,循环产生搜索基因并判断,若循环Repetition次后,“优良基因”个数不再增加,则停止循环。弹头数目越大,循环次数应增大。
由于搜索出来的“优良基因”存在某阵列的波达向量重复利用的情况,故需要在“优良基因”中进行二次筛选。通过计算机的搜索算法,得到各行元素相异的5组基因,组成矩阵。该矩阵的每一个列向量定位一个弹头运动轨迹,最终通过弹着点位置的计算得到5个弹头的定位结果。
该算法的原理框图如图2所示。
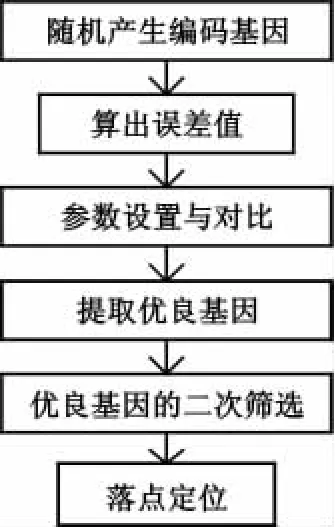
图2 算法原理框图Fig.2 The principle diagram of the algorithm
2 改进的多弹头落点定位算法
为解决文献[1]算法中敏感系数的设定需要根据弹头数目调整所带来的不便以及定位解算过程中因随机产生四维的列向量中易出现同一波达向量重复利用的现象,现将算法改进,具体如下:
2.1 算法原理
根据文献[3]利用正四面阵列组合采用DOA模型估计出弹丸弹道轨迹的原理以及编码基因的概念,若要确定弹丸的落点,首先要确定弹丸弹道轨迹方程。假设图1中组合的编码基因定位的是同一个弹丸的弹道,则图1中4个向量LA,LB,LC,LD所定位出的4个点A,B,C,D在同一直线上,可知向量AB、BC之间的夹角为180°,即。同理可得6个向量AB,AC,AD,BC,BD,CD中任意两向量之间的夹角为0°或180°,余弦值的绝对值为1。为充分利用数据,定义判决系数:
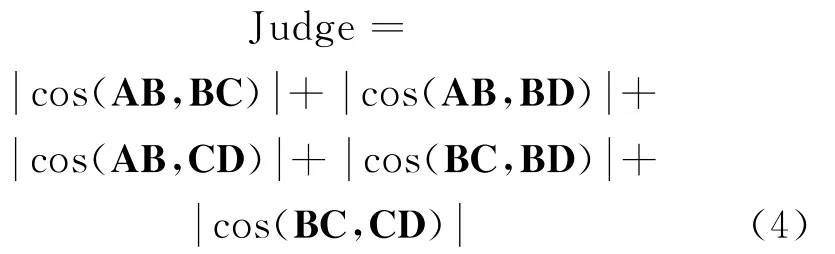
易知,理想情况下Judge=5时即可判定该4个点在同一直线上,即确定一条弹道线方程。弹道线方程选定后再根据Z轴的坐标值便可解算出弹丸落点。
算法的原理框图如图3所示。
2.2 改进型编码基因落点定位算法步骤
1)假设弹丸数目事先已知且为N,每一传感器均收到N个激波信号。由于不知道正确定位的波达方向向量组合,故每一个传感器阵列产生由[1,N]之间的整数随机排序的行向量。例如:N=4时,随机排序产生向量[4 2 1 3]。并将4个阵列所产生的随机数组合在一个4×N维的编码基因矩阵Matrix中。
2)循环解算出矩阵Matrix中由每一列编码基因所确定的空间定位点(Ai,Bi,Ci,Di)以及判决系数Judgei,i=1,2,…,N。假定当满足条件:Judgei>4.998时即可认为相应的编码基因为正确的编码基因,并保存在矩阵Right中,同时删除该编码基因在Matrix中相应的位置。Judge参数的设定可以避免原算法中敏感系数需要根据弹丸数进行调整的不便。
3)若矩阵Matrix为非零矩阵,则将该矩阵中每一行向量的元素重新随机排序,这样便可避免已存在矩阵Right中的编码基因出现,避免同一波达向量的重复利用,即避免原算法需要对优良基因二次提取的不便。重复步骤2)、3)。
4)若矩阵Matrix为零矩阵,则说明4个阵列分别得到的波达向量均很好地进行组合,退出步骤2)、3)的循环。最后对矩阵Right进行解算,得到定位点。
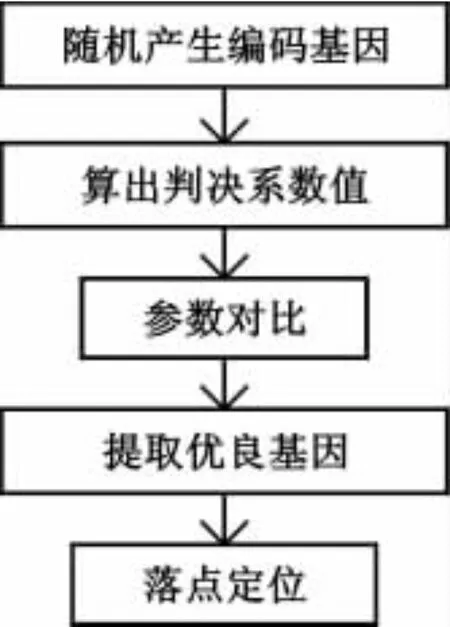
图3 改进算法的原理框图Fig.3 The principle diagram of the improved algorithm
3 多弹头落点定位仿真
按照蒙特卡罗法(Monte Carlo Methods)[4-5],对弹头散布进行多次仿真,弹头落点散布中心位置(xi,yi)有
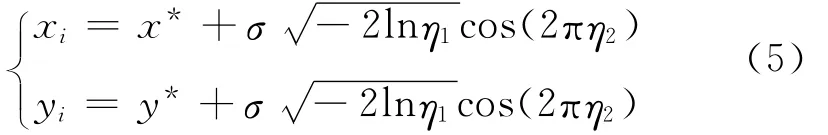
式(5)中,x*、y*为目标点,σ为弹头落点标准偏差,它与圆概率偏差CEP关系为:σ=0.849 321 80CEP。η1,η2为0~1之间的随机数。若为子母弹,第j颗子弹坐标为:
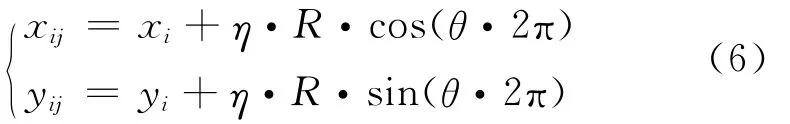
式(6)中,η和θ为0~1之间的随机数。R为子母弹抛撒半径。
本文将子母弹抛撒过程简化为母弹在解爆点解爆后,各子弹匀速飞向各自的落点。设置空中解爆点坐标:Location=[-500 0 1000];子母弹散布中心坐标:Center=[000];弹头数目:Num_Bull=21;子母弹抛撒半径:R=250;声速:Velocity_Sonic=340;子弹速度:Bull_Velocity=340×2.6。阵列中心坐标分别为:ArrayCenterA=[-200 400 0];ArrayCenterB=[-200-400 0];ArrayCenter_C=[200 400 0];ArrayCenter_D=[200 400 0]。
仿真过程中假设:
1)所有传感器均收到激波信号,若有重叠信号则经过理想分离得到所需信号;
2)超音速弹头在阵列敏感区域内匀速直线飞行;
3)各传感器精度满足要求;
4)探测信号过程中不受风等其他因素的干扰;
5)算法仿真20min之后不满足技术要求。
通过对原算法和改进的算法进行仿真,结果如表1所示(表中原算法的计算坐标为利用原算法仿真20min后的定位点,“*”表示未定位出坐标)。
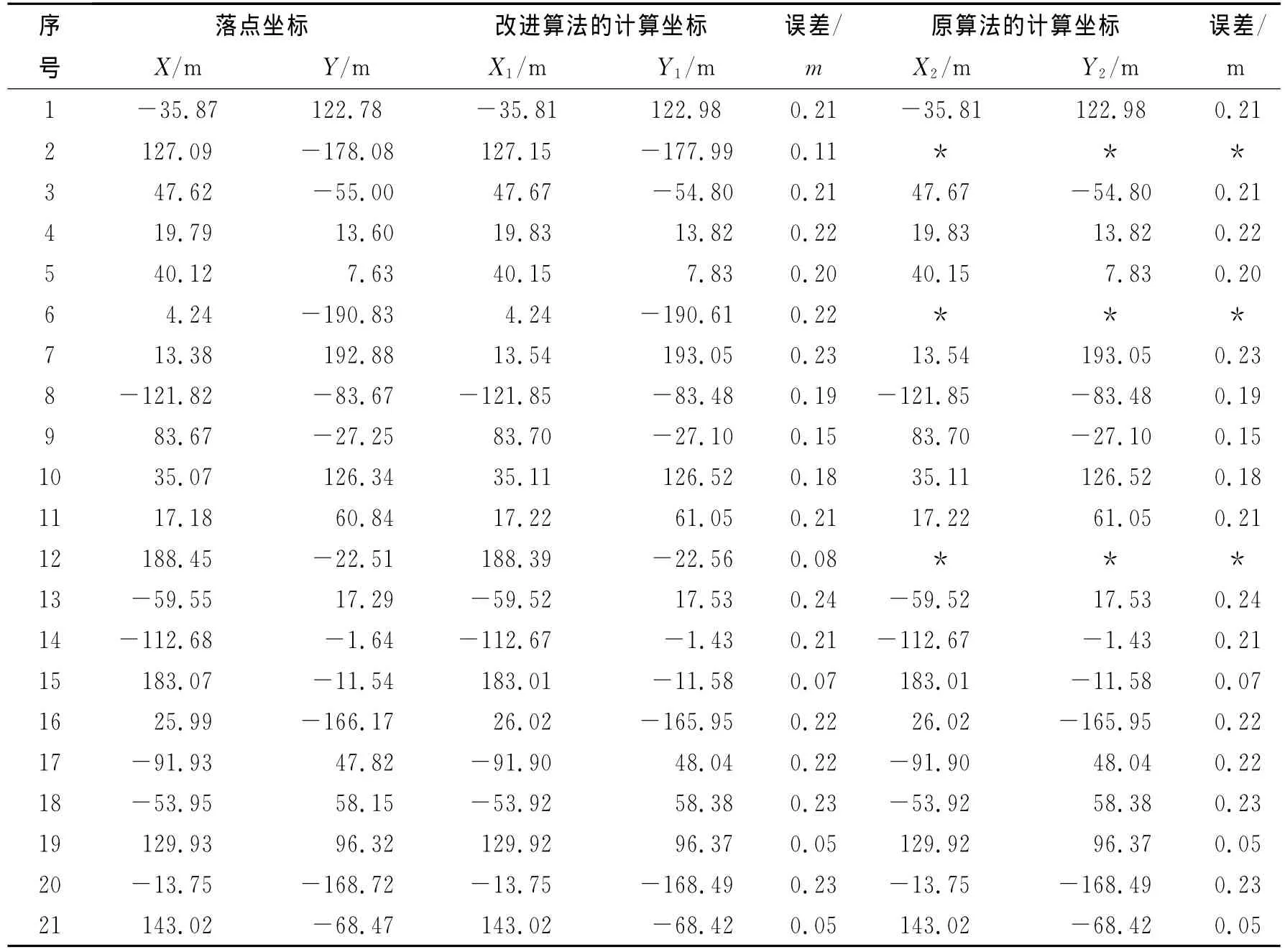
表1 弹头落点与计算落点坐标Tab.1 True and calculation coordinates of impact points
4 结论
本文提出了基于同一弹道线上4点决定的各矢量之间的夹角关系的改进型编码基因多弹头落点激波定位算法。该算法通过定义判决系数来提取满足要求的编码基因,当编码基因矩阵Matrix里的编码基因全部提取完毕时说明各阵列探测得到的波达向量已很好地组合并可用于定位落点。仿真表明:改进的定位算法可以很好地对落点进行定位,定位的最大误差为0.24m;解决了定位算法中因子弹数量过多而出现虚假定位点和程序易出现死循环的现象;避免了因弹头数量增减而需要调整敏感系数所带来的不便。算法的定位结果较为满意。但本算法所需的信号数据较为理想,如要运用到工程实践中还需进一步的研究。
[1]汪亮,王雪梅,陈昊明.基于编码基因的多弹头落点激波定位[J].探测与控制学报,2011,33(3):65-68.WANG Liang,WANG Xuemei,CHEN Haoming.Multiwarhead impact shock wave location based on genetic code[J].Journal of Detection & Control,2011,33(3):65-68.
[2]孙俊伟,张亚.低空超声速巡航导弹声探测研究[J].弹箭与制导学报,2008,28(4):45-48.SUN Junwei,ZHANG Ya.A study on sound detection of low altitude supersonic missile[J].Journal of Projectiles,Rockets,Missiles and Guidance,2008,28(4):45-48.
[3]蒋灏,罗晓松,冯策,等.利用DOA模型进行弹丸弹道轨迹估计[J].电声技术,2008,32(5):36-41.JIANG Hao,LUO Xiaosong,FENG Ce,et al.Trajectory determination of supersonic projectile using DOA model[J].Audio Engineering,2008,32(5):36-41.
[4]邱成龙.地地导弹火力运用原理[M].北京:国防工业出版社,2001:164-189.
[5]谭守林,张金巍,陈力.子母弹最佳抛撒半径与导弹精度关系研究[J].武汉科技大学学报(自然科学版),2010,33(1):109-112.TAN Shoulin,ZHANG Jinwei,CHEN Li.Relation between the best separation radius of submunition and missile’s precision[J].Journal of Wuhan University of Science and Technology,2008,32(5):36-41.
