基于人工蜂群改进算法的无线传感器网络定位算法

李牧东，熊 伟*，梁 青

(1．空军工程大学信息与导航学院，西安710077;2．西安邮电学院电子与信息工程系，西安710121)

位置信息对传感器网络的监测活动至关重要，没有位置信息的监测消息毫无意义[1]。如何确定无线传感器网络中节点的位置信息，成为了必须解决的关键问题。现有的无线传感器网络定位技术大体可分为基于测距和非测距两类[2]。

DV-Hop算法是目前最受关注的无需测距的定位算法之一[3－4]。目前，已有很多关于经典 DV-Hop的改进算法，文献[5]提出了通过先计算锚节点间的平均跳距得出误差后再对网络的平均跳距进行修正的方法;文献[6]通过利用RSSI技术完成对未知节点与锚节点间距离的测量，从而提高了定位精度;文献[7]对平均跳距进行加权处理并有选择地选取锚节点进行定位从而减小定位误差;文献[8]将人工蜂群算法引入到DV-Hop算法未知节点计算阶段从而提高了定位精度。

本文针对DV-Hop节点定位算法中采用多边测量法计算未知节点坐标时产生较大误差的问题，把节点定位问题转化为最优化求解问题，结合人工蜂群算法(Artificial Bee Colony，ABC)的特点，在文献[8]的基础上，提出了自适应蜂群算法并将其应用于未知节点坐标的计算阶段，以期减小定位误差。

1 问题描述

DV-Hop算法是由Niculescu等人提出的，其定位过程分为3个步骤[3]:首先，使用典型的距离交换协议，使网络中所有节点获得距锚节点的最小跳数;其次，锚节点计算网络平均跳距，并采用可控洪泛法广播至整个网络中，即每个节点仅记录接收到的第1个平均跳距信息，而忽略之后接收到的;最后，通过未知节点通过所记录的平均跳距和最小跳数信息计算自身到相应锚节点的距离，利用三边测量原理或极大似然估计原理计算自身坐标。

在DV-Hop算法中，锚节点的平均跳距计算公式[4]如下

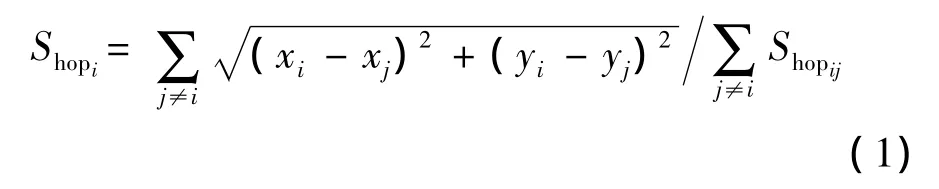
其中:Shopi是锚节点i对应的平均每跳距离，j为锚节点i数据表中的其他锚节点号，Shopij为锚节点i和j之间的跳数。

未知节点接收到平均跳距后，跟据所记录的跳数信息，通过式(2)计算其到锚节点的距离:

通过上述计算后，传统DV-Hop算法利用多边测量法求解未知节点的坐标，从而完成定位，如图1所示。

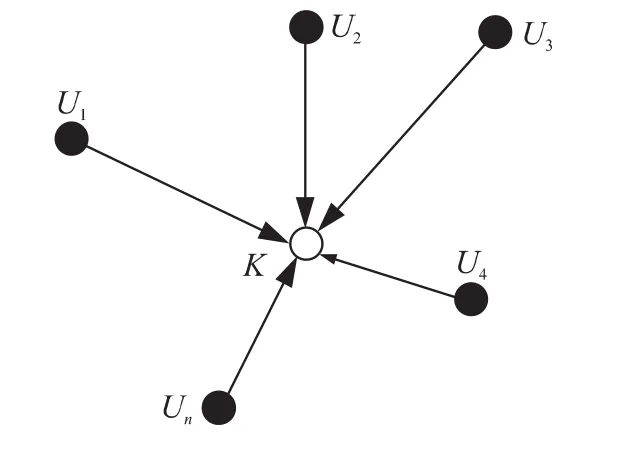
图1 多边测量法示意图

若已知在n(n≥3)个锚节点时，U1(x1，y1)，U2(x2，y2)，…，Un(xn，yn)以及它们到未知节点 K(x，y)的测量距离分别为 d1，d2，…，dn，则有

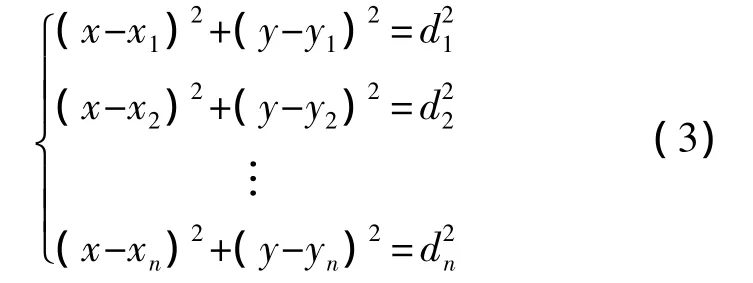
用方程组的前n－1个方程减去第n个方程后，得

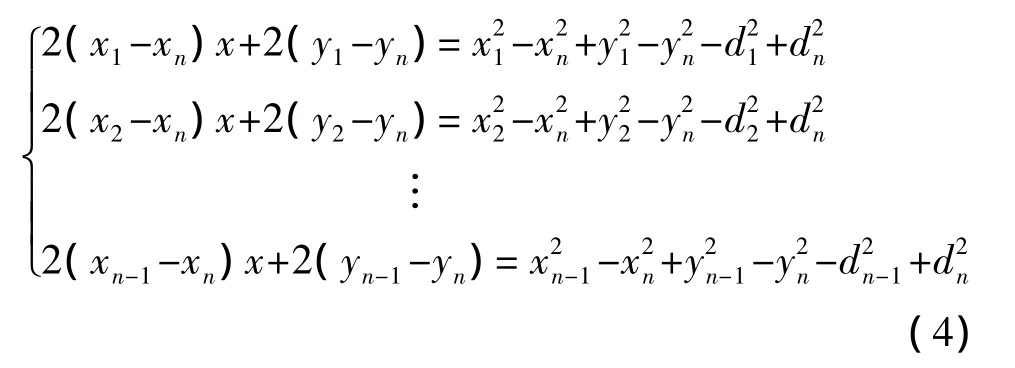
用线性方程组表示为AL=b，其中L=(x，y)T，

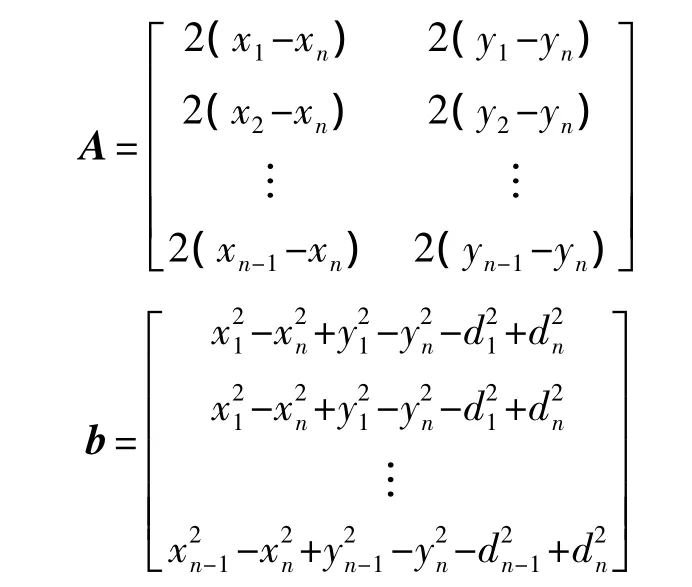
由于测距误差、环境因素、通信等影响，测量距离总存在一定误差，因此合理的线性方程组应该是AL+ε=b，ε为n－1维随机误差向量。使用标准的最小二乘法可以得到方程组的最小二乘解为L=(ATA)－1ATb。由于向量b中的每个元素都包含dn，而dn是带有误差的测量距离，因此所计算出结果的准确程度受制于dn。如果dn的误差足够小，那么求得的向量L还能满足要求;若dn的误差本来就很大，则求得的解的误差也将很大。该方法虽然简化了求解非线性方程组的过程，却有可能牺牲解的精度，针对此情况，本文把问题转化为全局最优化求解问题。

假设fn为未知节点到锚节点之间的测距误差，则再由式(3)可知，对于未知节点坐标(x，y)满足下式:

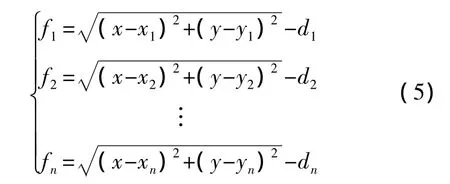
求解(x，y)，使得

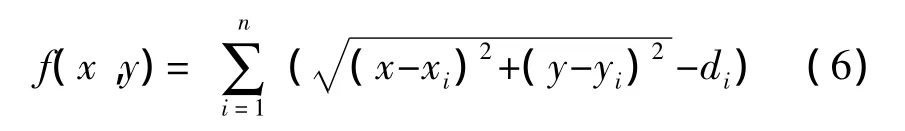
求解过程中，当由式(6)计算出来f(x，y)取最小值时，总误差最小，则(x，y)的解最接近真实值，而此时的坐标(x，y)为最优解。由式(5)可知，f(x，y)的解不受限于某个方程，即当某个锚节点的测距误差较大时，对于(x，y)的最终解影响也不大。

如上所述，便把节点定位问题转化成全局最优化求解问题。对于式(6)的求解是个非线性最优化问题，如果用传统的数学方法求解是很困难的。而人工蜂群算法是用来解决最优化问题中较为高效的方法，实验结果表明，用人工蜂群算法求解最优化问题是行之有效的[9]。

2 改进人工蜂群算法求解最优化定位

2．1 ABC算法描述

人工蜂群算法ABC(Artificial Bee Colony)是由土耳其埃尔吉耶斯大学Karaboga在2005年提出的一种基于蜜蜂群智能搜索行为的优化算法[9]。在蜂群算法中，按照分工可将蜂群分为3类，即引领蜂、跟随蜂和侦查蜂，其中引领蜂和跟随蜂各占一半，并且引领蜂与蜜源的数量相等，用SN表示。首先，ABC算法初始化生成含有SN个蜜源(解)的初始蜂群;然后，引领蜂对所有的蜜源进行循环次数为C(C=1，2，…，N)的循环搜索，如果搜索到的蜜源的花蜜数量(适应度)优于以前的，则用新的蜜源位置代替旧的蜜源位置，否则保持旧的蜜源位置不变;最后，所有的引领蜂完成搜索之后，回到舞蹈区把蜜源上的信息分享给跟随蜂，跟随蜂则根据得到的信息依据贪婪机制选择较优的蜜源。跟随蜂选中蜜源后，也进行一次邻域搜索，并保留较好的解。式(7)为引领蜂和跟随蜂进行蜜源位置更新的公式:

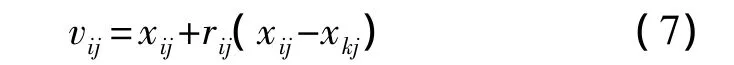
其中k为不同于i的蜜源，j为随机选择的下标，且k不等于 i，rij∈[－1，1]是一个随机数，它控制 xij邻域的生成范围，随着搜索接近最优解，邻域的范围会逐渐减小。ABC算法中跟随蜂对蜜源的选择是通过判断蜜源的收益率大小来确定的，收益率通过适应度值来表示，选择概率Pi按照式(8)确定，其中fiti是第i个解的适应度值，SN是解的个数。

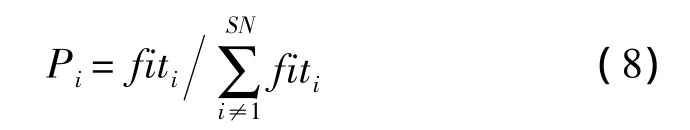
假定蜜源连续经过限定次数循环之后仍没有得到改善，表明这个解陷入局部最优，那么这个位置就要被放弃，该位置的引领蜂转变为侦查蜂。限定次数是ABC算法中重要的控制参数，用来控制对侦查蜂的选择[10]。假设被放弃的解是xi，侦查蜂发现新位置并代替xi的操作如下。

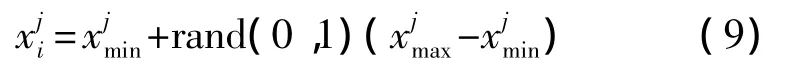
2．2 人工蜂群算法改进

人工蜂群算法中引领蜂对蜜源的搜索阶段是影响整个算法全局及局部搜索能力的重要阶段，在传统人工蜂群算法中，由于rij的设置仅是在[－1，1]之间的随机数，而没有考虑引领蜂与跟随蜂在位置更新时存在的联系，具有较大的随机性，从而导致在寻优求解过程中存在收敛速度慢、搜索精度低的缺点，严重影响了算法的性能。文献[8]提出的基于人工蜂群算法的DV-Hop改进算法虽然在一定程度上提高了定位精度，但由于人工蜂群算法本身的局限性，算法的定位精度还有待进一步提高。本文在受到文献[11]的启发，对式(7)即引领蜂和跟随蜂进行蜜源位置更新的公式，在文献[8]的基础上，引入自适应思想，提出了自适应人工蜂群算法AABC(Adaptive Artificial Bee Colony Algorithm)。

在引领蜂与跟随蜂进行位置更新时，较大的rij有利于跳出局部极小值点，而较小的rij有利于算法的收敛[12]。对全局搜索通常较好的方法是在算法的初期使用较大的rij以通过较高的探索能力得到较优的蜜源，提高其搜索的精度，而在后期则需要较小的rij值，来提高算法的局部搜索能力以加快其收敛速度。因此将rij设计为迭代次数的函数，且随着迭代次数逐渐递减，并考虑到引领蜂与跟随蜂的关系，将rij设置如下:

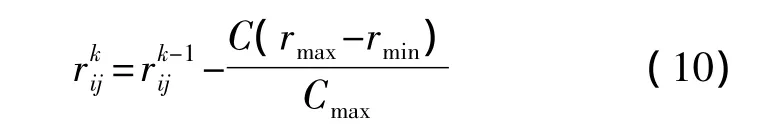
其中，rmin、rmax分别为初始和终止权重，Cmax为最大迭代次数，C为当前迭代次数。则引领蜂与跟随蜂进行蜜源位置的更新公式改为:

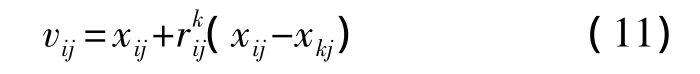
由此对蜜源位置的搜索趋势起到了一定的引导作用，克服了算法本身随机性强、收敛速度慢的缺陷。因此根据式(6)，定义本文适应度函数为:

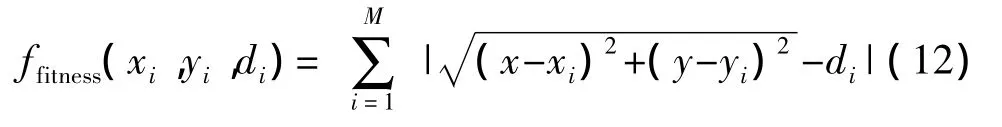
其中，M为锚节点个数，则AABC算法主要步骤如下:

步骤1:设置主要初始参数:种群数、最大循环次数、参数维数、阈值等，其中引领蜂和跟随蜂各占50%，侦查蜂1个;

步骤2:随机产生SN个初始蜜源;

步骤3:引领蜂搜索蜜源，并根据式(12)计算蜜源适应度值，进入循环;

步骤4:跟随蜂分享蜜源信息，由式(8)选择其中一个蜜源，然后按式(11)搜索临近新蜜源;

步骤5:对新蜜源计算适应度值，并根据贪婪机制选择更优的蜜源;

步骤6:若循环至限定次数后，蜜源适应度值仍不达标则放弃，引领蜂变成侦查蜂继续搜索，由式(9)更新位置;

步骤7:存储此时的最优解;

步骤8:循环次数加1;

步骤9:满足终止条件，达到最大循环次数。

2．3 结合AABC算法的DV-Hop改进

假设在一个无线传感器网络中总共存在N个节点，其中M个锚节点、N－M个未知节点，且锚节点坐标已知。根据DV-Hop算法原理，结合其定位过程，将AABC算法引入到 DV-Hop算法中，记为ADV-Hop，则基于AABC算法的DV-Hop算法定位流程如图2所示。

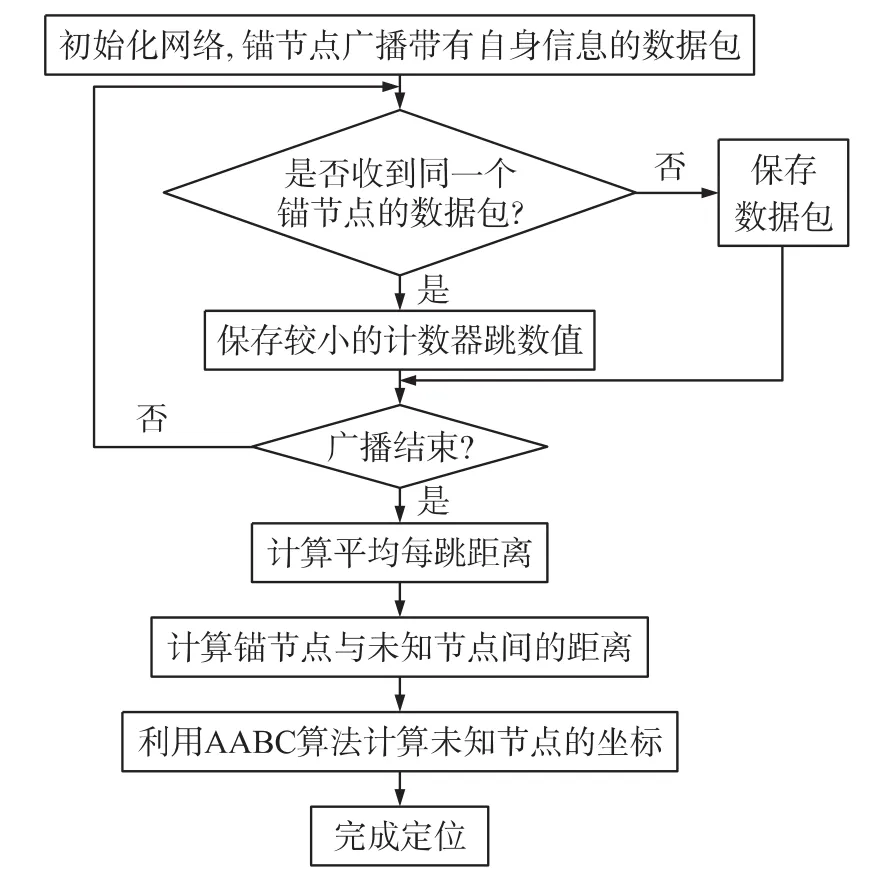
图2 ADV-Hop算法的定位流程

3 性能分析

本文的实验在Matlab平台上进行，由于无线传感器网络节点受到体积、能量的限制，为了最大程度地减小本文改进算法ADV-Hop的定位误差及能量消耗，设置循环次数C=30，引领蜂和跟随蜂总数SN为50，且各占总数的一半，控制参数限定次数为10，rmin=0．4，rmax=1．2，r初始值设为 1，阈值 ε =10－6。假设所有锚节点坐标已知，节点随机分布在边长为100 m的方形区域内;未知节点和锚节点的坐标随机产生;每个节点的通信半径R=21 m。

假设各次仿真时的网络区域、节点总数、锚节点总数、节点通信半径等网络参数相同，仿真次数为k=500，锚节点个数为m，节点个数为N，定位节点的真实坐标为，用统计的归一化平均定位误差、平均定位误差均方差作为定位算法精度和稳定性的衡量指标。设ej、σj分别为仿真1次时的平均定位误差和定位误差均方差[13]。则基于k次仿真结果统计的归一化平均定位误差及归一化的平均定位误差的均方差分别为:

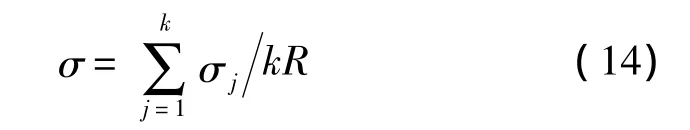
为了客观地分析本文改进算法的定位性能，本实验将文献[8]提出的基于ABC算法的DV-Hop改进算法(记为BDV-Hop)，与利用最小二乘法计算未知节点的DV-Hop算法[4]一起，通过500次仿真实验，与本文改进算法ADV-Hop进行比较。

图3给出了100个节点随机分布在方形区域内锚节点比例在5% ～40%变化时，归一化平均定位误差变化情况;图4给出了相同条件下锚节点比例变化时，归一化的定位误差均方差的变化情况。从图3、图4可以看出:在节点总数和节点通信半径不变的情况下，3种算法的平均定位误差和均方差都随着锚节点比例的增加而减小;另外，在相同条件下，ADV-Hop的平均定位误差和均方差都明显小于DV-Hop和BDV-Hop，具体的本文改进算法 ADVHop分别比DV-Hop归一化的平均定位误差平均减小了34．37%，较BDV-Hop平均减小了17．95%;而对应的归一化的定位误差均方差平均减小了21.58% 和 7．83%。

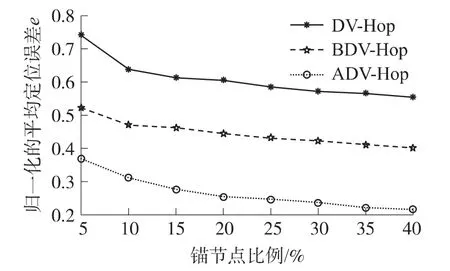
图3 锚节点比例与归一化的平均定位误差关系

图4 锚节点比例与归一化的定位误差均方差关系

图5和图6是在网络区域内随机选取10个锚节点，节点总数分别取 100、150、200、250、300、350、400时，各个算法的定位性能比较。从图5、图6可以看出，在锚节点不变的情况下，3种定位算法的定位误差、定位误差均方差都随节点个数的增多而逐渐减小。ADV-Hop的定位误差较DV-Hop平均减小了25．68%，较 BDV-Hop减小了10．15%，相应的误差均方差分别平均减小了20．27%和7．38%。

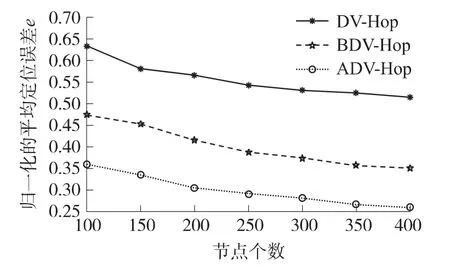
图5 节点个数与归一化的平均定位误差关系

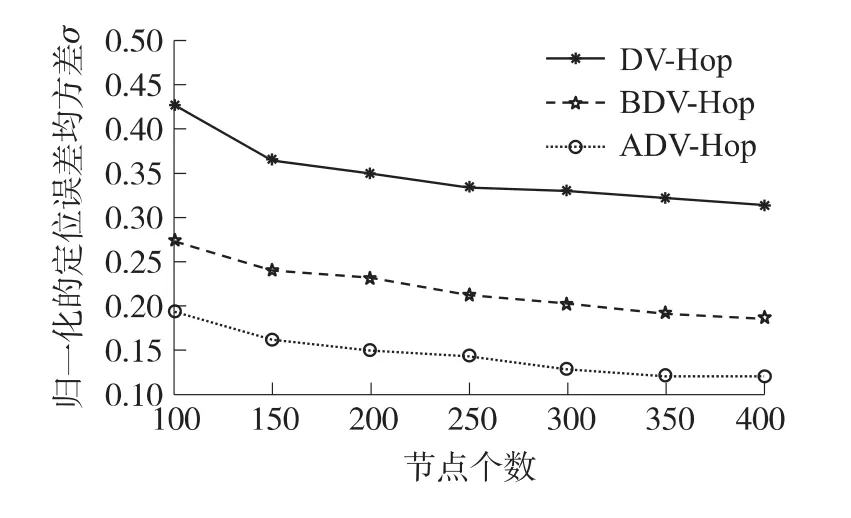
图6 节点个数与归一化的定位误差均方差关系

从以上的结果分析中可以看出BDV-Hop算法在定位精度和稳定性方面都优于传统DV-Hop算法，说明了将人工蜂群算法应用于无线传感器网络节点定位是一种可行的方案，另外相比于BDV-Hop算法，改进的ADV-Hop算法在定位精度和精度稳定性方面都有较大改善，有效地提高了算法的全局搜索能力以及收敛速度。

4 结束语

节点定位是无线传感器网络的应用基础。本文在详细分析DV-Hop算法中定位阶段利用多边测量法计算未知节点坐标过程的基础上，成功将节点定位问题转化为最优化求解问题，并利用ABC算法在解决最优化问题的优势，结合定位具体问题，对ABC算法进行了改进，提出了基于改进ABC算法的ADV-Hop算法。该定位算法实现简单，运行稳定，并且能够有效地解决传统DV-Hop算法采用多边测量法估计未知节点坐标时定位误差较大的问题，提高了算法在定位过程中的定位精度以及稳定性。仿真结果表明，ADV-Hop算法在不增加硬件开销及略微增加计算开销的基础上，相比于传统DV-Hop算法及BDV-Hop算法，在不同锚节点数和节点个数的条件下，明显改善了算法的定位性能。

[1]Akyildiz I F，Weilian Su，Sankarasubramaniam Y，et al．A Survey on Sensor Networks[J]．IEEE Communications Magazine，2002，40(8):102－114．

[2]张震，闫连山，刘江涛，等．基于DV-Hop的无线传感器网络定位算法研究[J]．传感技术学报，2011，24(10):1469－1472．

[3]姜钧，程良伦．采用虚拟锚节点的高精度VAD-Hop定位算法[J]．传感技术学报，2011，24(7):1048－1052．

[4]Niculescu D，Nath B．Ad-Hoc Positioning System(APS)[C]//Proceedings of the 2001 IEEE Global Telecommunications，2003，1734－1743．

[5]Dongxiao Liu，Yujun Kuang，Wei Wei．Research and Improvement of DVHOP Localization Algorithm in Wireless Sensor Networks[C]//Proceedings of International Conference on Computational Photography，2010，47－50．

[6]Fang Wangsheng，Yang Guangyu．Improvement Based on DV-Hop Localization Algorithm ofWirelessSensorNetwork[C]//Proceedings of International Conference on Mechatronic Science，Electric Engineering and Computer，2011，2421－2424．

[7]刘文远，王恩爽，陈子军．无线传感器网络中DV-Hop定位算法的改进[J]．小型微型计算机系统，2011，6(6):1071－1074．

[8]李牧东，熊伟，郭龙．基于人工蜂群算法的DV-Hop定位改进[J]．计算机科学，2013，40(1):33－36．

[9]Karaboga D．An Idea Based on Honey Bee Swarm for Numerical Optimization，Technical Report-TR06[R]．Kayseri:Erciyes University，Engineering Faculty，Computer Engineering Department，2005．

[10]Karaboga D，Basturk B．On the Performance of Artificial Bee Colony(ABC)Algorithm[J]．Applied Soft Computing，2008，8(1):687－697．

[11]陈贵敏，贾建援，韩骐．粒子群优化算法的惯性权值递减策略研究[J]．西安交通大学学报，2006，40(1):53－56．

[12]Lei Xiujuan，Huang Xu，Zhang Aidong．Improved Artificial Bee Colony Algorithm and Its Application in Data Clustering[C]//Proc．of 2010 IEEE Fifth International Conference on Bio-Inspired Computing:Theories and Applications，2010，514－521．

[13]林金朝，陈晓冰，刘海波．基于平均跳距修正的无线传感器网络节点迭代定位算法[J]．通信学报，2009，30(10):107－113．