“引而有导”在解决问题中发展数学能力

骆超

数学课堂教学是学生丰富的数学思维活动的展示平台，学生在解决问题的过程中，每个人都会有自己对问题的理解，并在此基础上形成解决问题的基本策略。教师如果在包容中，鼓励学生个性的张扬，学生的创新精神与能力的培养就成为了可能。而这样做的意义更在于为学生的思维活动创设了时间与空间，给予了自由表达问题解决的机会，提升了问题思考的价值取向。

课堂教学中，面对同一个问题的解决总会出现一些这样或那样的想法，而这个时候正是我们培养学生能力的重要时机。如何来正确面对学生的想法，如何来进行有效的指导，如何来开展正确的评价，都是我们不得不面对的一个问题。下面，我以《面积》教学的片断及反思为例，谈谈数学学习中学生解决问题所具有的一些特点及教师引导的方法。

【片断展示】

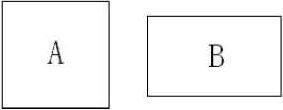
教师引出了异类形状图形（长方形与正方形）面积大小的比较，这无疑是一个具有挑战难度的问题。

师：同学们，仔细观察下面两个图形的面积大小，你能说说哪个图形的面积比较大吗？为什么？

学生困惑之情溢于言表。

师：那大家四人小组先讨论交流一下，呆会儿我们再来汇报。

小组活动……

生1：我觉得还是可以用重叠的方法来比较的。

师：怎么比较呢，说来听听。

生1：（学具操作）比较多出的部分面积大小，我发现正方形的面积比长方形的面积大。

师：大家同意这样的比较方法吗？

生：同意。

生2：我觉得还是用尺子量的方法比较简单。我量出来正方形是16厘米，长方形是16厘米。所以，两个图形的面积应该是一样的。

生：不对！不对！这样比的是周长，不是面积。

师：刚才这位同学说用尺子量的方法看来行不通，还有其他的方法吗？

生3：老师，我觉得用书上“摆硬币”的方法挺好的。

师：哦，那我们看看书上的“摆硬币”方法吧。

生：这方法好是好，但我们没有这么多的硬币呀？

生4：老师，我有好办法了，不需要很多的硬币的。

师：哦，说来听听。

生4：我还是用重叠的方法。只要比多余部分就可以了正方形多余部分摆4个硬币，长方形多余部分摆3个硬币。所以正方形面积要比长方形面积大。

师：这样的方法大家觉得好吗？

生：好。

师：还有要表达自己意见的同学吗？

生5：老师，其实我觉得用摆硬币的方法还是挺麻烦的。我觉得用画格子的方法会简单些。

师：你准备怎么画格子呢？

生5：在两个图形里面画上相同大小的正方形小格子，看哪个图形画的格子多，就那个图形的面积大。

师：拿起准备好的两个图形纸片，我们一起试着画一画吧。

学生活动……

师：介绍一下你们的画法吧。

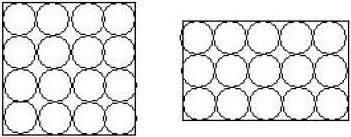
生6：我将两个图形分解成了大小一样的小正方形格子，正方形的纸片一共画了16个，长方形纸片一共画了15个。所以正方形的面积比长方形的面积大。

【反思】

1.合理创设认知冲突，使之成为问题解决的生长点。认知冲突多产生于学生的思维与学习材料相互作用所形成的问题情境。对于同类形状的图形的大小比较，学生有一定的认知基础，能够形成一些解决问题的共识；但由于异类形状图形的出现，在一定程度上造成了学生的认知冲突，所以学生的困惑产生也是可以预见的。而这种冲突点的出现是学生能力发展的重要契机。所以，作为教师来说，必须吃透教材，了解学生，充分利用教材内在的矛盾因素和学生认知的特点设置问题情境，激发学生的认知冲突。

2.提供探究操作环节，使之成为问题解决的踏脚石。学生解决问题策略的一个重要特点是，将外显的动作过程与内隐的思维活动紧密结合起来，使之成为“思维的动作”和“动作的思维”。同时，操作活动是一个动态过程，它顺应了小学生好奇好动的心理特点，又可集中注意，激发兴趣。教师在教学过程中要特别重视学生的探究操作环节，让学生在学习中动手，在动手中学习，使问题解决过程真正成为互动有效的学习内驱力。

3.让学生经历“比较——反思”的“最优化”思维过程。生1利用重叠的方法来验证图形面积的大小，源于前面对相同形状图形面积大小的判断基础。生2用了尺量的方法来判断图形面积的大小，显然他是将面积和周长的大小判断发生了混淆。生3的方法虽然取自于书本，但从另一个方面来说，原有的生活经验是形成这样一个方法的基础。与生4的方法比较，我们也不难发现，学生在操作中更加关注了方法的比较与选择。对于比较面积大小这一问题，学生知道用摆硬币的方法对于小图形可能是好方法，对于大图形的面积却不一定适用。生5的所提出的是判断面积大小的最佳方法。形成这个方法的过程也说明，学生的思维过程是一个由操作作为基础，由离散逐步趋向统一的过程。经过前面一些方法的积累，学生逐渐将最优法形成。教学中，如何引导学生将解决问题的策略进行“最优化”处理，是促进学生能力发展的重要环节。

我们应该充分关注并了解学生的问题解决过程，研究学生的认知和心理特点，培养学生形成一些基本的问题解决策略，引导学生体验问题策略的多样性，为学生的可持续发展奠定坚实基础。