在几何教学中培养学生的思维能力

刘君

中图分类号：G633.6 文献标识码：B 文章编号：1006-5962（2013）06-0226-01

《数学课程标准》（2011年版）指出："数学教学活动，特别是课堂教学应激发学生兴趣，调动学生积极性，引发学生数学思维，鼓励学生的创造性思维"、"建立数感、符号意识和空间观念，初步形成几何直观性和运算能力，发展形象思维与抽象思维"。课标这一基本观念，凸显了思维能力的培养在小学数学教学中的重要地位。为此，小学数学教学必须将学生思维能力的培养落实到具体的教学之中，为提高学生的思维能力引路搭桥。下面就几何教学中如何培养学生的思维能力谈几点做法：

1 激发兴趣，诱发思维激情

兴趣是从事任何活动最积极的心理因素，是一种特殊的意识倾向，是产生动机的主要原因。学习兴趣又与思维发展有着密切的联系，是互为统一的两个方面，思维是萌发兴趣的动力，兴趣则是促进思维活动的前提。因此在数学教学中，激发学生学习兴趣尤为重要，那么在几何教学中怎样激发学生的兴趣呢？我认为点燃学生心中探求知识的好奇之火，利用好奇心理创设情境，是激发学生学习兴趣，诱发学生进行思维活动的重要手段。

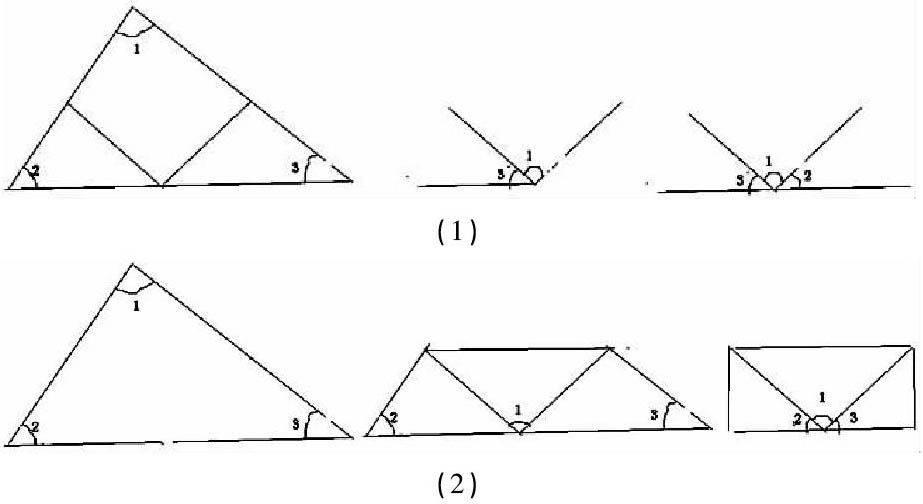
例如，学习"三角形的三个内角和是180度"这节课，在揭示了各种三角形的图形之后我说："只要你们先把量出来的任何一个三角形的两个角的度数告诉我，我马上就能知道第三个内角的度数"。我的话音刚落，学生在好奇心的驱使下，马上拿出了量角器，通过度量后纷纷举手说出自己所量的两个内角的度数，我亦马上回答他们第三个内角的度数，他们通过自己的验证，得出老师回答得很正确，这时，学生显得十分惊讶：老师怎么这么快就知道第三个角的度数啊！怎么知道的呢？求知欲开始萌发，于是，我趁热打铁，让大家通过拼图（见图（1））、折图（见图（2））：

得知三个角的度数之和是180度，即三角形的内角和是180度。

又如，在学习平行四边形面积时，我先出示了一个平行四边形的纸板，问学生："谁能想出办法把平行四边形剪拼成长方形？"学生拿出自己准备好的平行四边形，怀着极大的兴趣，带着老师提出的问题，全神贯注地投入到拼剪活动之中，通过剪拼他们分别拼成如下几种图形：

剪拼完后他们又争先恐后让老师看他们剪拼的图形，尤其是与别人剪拼不同的学生，更是希望老师看到他们的成果，此时，学生的兴趣极浓。于是我接着问："拼成的长方形的长、宽与原来的平行四边形的底、高之间有什么关系呢？"这里我抓住了知识的关联因素，运用迁移规律，帮助学生寻找新旧知识的连接点和新知识的生长点。学生纷纷汇报结果，答出长方形的长是平行四边形的底，长方形的宽是所拼图形之前平行四边形的高，从而推导出求平行四边形的面积公式。

通过这些教学实践使我认识到，思维活动的积极性，常常是由在实践中碰到的要解决的问题所引起的，因此动手操作，创设情境，激励学生发现问题，是诱发学生思维的重要途径。

2 动手操作，培养思维能力

几何知识是抽象的，而小学生的思维又处于以具体形象思维为主，逐步向抽象逻辑思维过渡阶段，如何做好这一过渡呢？在教学中，我通过学生动手操作，让学生在做一做、拼一拼、摆一摆、量一量、画一画中，把抽象的几何知识具体化，形象化。在动手操作中培养学生的思维能力。

如学习了长方体的体积之后，我让每个学生用十二个一立方厘米的正方体摆出体积是十二立方厘米的长方体，看看有几种摆法，学生根据长方体计算公式摆出了各种图形（计8种），并很快得出体积，列出如下多个算式：

（1）4×3×1 （2）2×3×2 （3）3×2×2 （4）12×1×

（5）3×1×4 （6）2×1×6 （7）6×1×2 （8）1×1×12

这样，学生通过自己的拼摆，不但加深了对长方体体积计算公式的理解，同时又进一步明确了虽然体积形状变了，但体积大小没有变，物体所占空间的大小没有变。这样，不但深化了体积的概念，而且学生的分析综合能力得到了发展，同时对书中 "一个正方体溶积是216立方分米，把这一箱油倒入另一个长方体内，已知长方体的油箱长8分米，宽5分米，这油箱中油深多少米？"这一难题找到了解决的途径，并加深了理解。

又如，学习了圆的面积之后，我出示了一道求阴影面积的图形（如图（1）），刚开始学生举手回答的人数不多，这时我让学生每人在一正方形纸上画一个最大的圆（如图（2）），然后问学生这个图形阴影面积会求吗？同学抢着回答，于是我又让学生将图（2）对折成图（3）

再将对折后的图（3）剪成4个一样的图形让学生拼摆，看能拼摆成几种图形，结果，学生拼摆出如下图形：

通过剪拼，同学们既动手又动脑，灵活的双手使脑的功能得到了发展，变得很聪明，聪明的头脑又使手的技能得到了训练，变得灵巧了。这时同学们争着抢着交流着他们的感受，脸上露出了满意的微笑，我问"这些图形阴影面积会求吗？"同学们异口同声地回答说："是正方形面积减去圆的面积"。可见学生已掌握了由具体到抽象，由特殊到一般的思维方法，并且已经初步形成了概括的能力。我接着又问："这样说严密吗？"一名学生回答："这些图形阴影部分的面积是一个正方形的面积减去一个直径与正方形边长相等的圆的面积。"从学生的实际操作及对问题的正确回答中，可以看出，通过多种感官的协调活动，不但激发了学生思维的积极性，而且借助语言的表达，又加深了对事物的深刻理解，其概括能力也得到了发展。

总之，从小学数学教学过程来看，学生数学知识和技能的掌握与思维能力的发展是密不可分的。一方面，学生在理解和掌握数学知识的过程中，要不断地运用着各种思维方法和形式。如比较、分析、综合、抽象、概括、判断、推理等，另一方面，在学习数学知识时，又为运用思维方法和形式提供了具体的内容和材料。因此，在几何教学中教师要有意识、有计划地将思维能力的培养寓于数学知识的教学之中并贯穿于数学教育的始终。