滑窗Prony算法的时变振荡特性分析方法

杨利波，杨芳

(1．湖南省电网工程公司，湖南 衡阳 421002;2．广东电网清远供电局，广东 清远 511500)

滑窗Prony算法的时变振荡特性分析方法

杨利波1，杨芳2

(1．湖南省电网工程公司，湖南 衡阳 421002;2．广东电网清远供电局，广东 清远 511500)

Prony算法可以提取平稳信号的振荡频率和阻尼，但不能正确反映时变信号的振荡特性。而现实的低频振荡往往具有多模式时变的特点，而且存在模式复合现象。提出滑窗Prony算法分析时变振荡信号，通过窗口滑动观察振荡信号的时变特点。算例说明，滑窗Prony算法能较好的分析低频振荡的多模式的时变特性，更适合实际电力系统振荡信息分析。

电力系统;低频振荡:窗口滑动:Prony

1 引言

电力系统低频振荡过程中往往共存着多个不同的振荡模式，不同模式的起振和平息时间各不同，而且各模式之间存在着相互作用，复合或激发出新的振荡模式。也就是说，电力系统低频振荡中存在着时变特性［1－3］。

文献［1］指出电力系统中存在多个起止时间不同的振荡模式。文献［2］指出实际电网的低频振荡中存在2个或多个模式叠加的现象。文献［3］指出小干扰下各振荡模式间相互作用会产生新的振荡模式，并且新产生的振荡模式间同样存在相互作用产生更加复杂的振荡模式。

电力系统低频振荡频率一般在0.2～2.5Hz［4］之间。利用现场实测数据进行信号处理分析、得到振荡特征参数是电力系统低频振荡研究的一种有效途径［5－7］。在分析实测数据并进行低频振荡识别时，现有的方法主要有实时 FFT 算法［7］、小波算法［8］、Prony算法［9］等。实时FFT算法精度受数据窗限制，不能反映振荡的阻尼特性;小波算法可以反映信号的时变特性，但存在小波基难以选取的问题;Prony算法能直接提取幅值、相位、频率和衰减因子，算法简便，因此被用于电力系统低频振荡的模式识别［10－15］。但是实际电力系统的低频振荡信号往往具有多模式且时变的特性，而且存在模式复合现象，利用基于线性的prony算法识别振荡模式将会出现很大的误差。

鉴于此，本文提出了基于滑窗prony算法的时变特性分析。通过对滑动窗口内的模式变化分析，得出信号的时变特性规律。并通过对起止时间不同的模式和模式之间复合现象的算例进行分析，表明了该算法的有效性和准确性。

2 滑窗Prony算法

Prony方法采用p个具有任意幅值、相位、频率和衰减因子的指数函数的线性组合对振荡数据等间距采样，提取振荡特征，进行模式识别。

假设采样信号共有N个原始数据即为x(n)(n=0，1，2，…，N－1)。令M为每次滑动窗口的长度，i为滑动次数，m为滑动总次数，以每次滑动d个采样点。定义^x(i)(n)为第i次窗口滑动时x(i)(n)的近似值，i=1，2，…，m

构造目标函数如下

Prony算法的关键是避免求此复杂的最小二乘解，认识到(1)式的拟合是(4)的齐次解。

阶数p根据AR模型的SVD分解定义归一化奇异值kk来确定［15］。

根据(4)递推出^x(i)(n)，并将(1)所表示的振荡拟合模型写成矩阵形式

Z(i)是范德蒙德矩阵。可以据(8)求得最小二乘解为

将z(i)k代入(1)得到振荡频率和衰减因子，将(9)代入(1)得到振荡的幅值和初相为

3 滑窗prony算法改进

传统的滑窗Prony方法受到阶数，采样频率，滑动窗长的选择和滑动次数的确定等因素的影响［16］，实际应用中对其进行如下改进:

(1)采样频率fs过低容易导致频谱混叠，过高则易造成运算速度降低，甚至参数估计精度下降。低频振荡关注频率为0.1～2.5Hz，所以一般取1.0 Hz。

(2)滑动窗长的选择直接关系到每次所包含的有效信息，试验表明窗长选取5～8s较合理。

(3)如果窗口内包含时变特性时，prony识别结果会随着窗口滑动不断变化，直到窗口时间段内的信号平稳，识别结果主导模式的频率、衰减因子、相位将不再变化，幅值将以指数衰减变化，即为此时的主导模式。

4 仿真算例

4.1 算例1

为模拟振荡模式起至时间变化不同的情况，构造一个由3个时间段组成的信号［8］，具体参数如表1所示。表2和表3分别为prony和滑窗prony算法的分析结果。

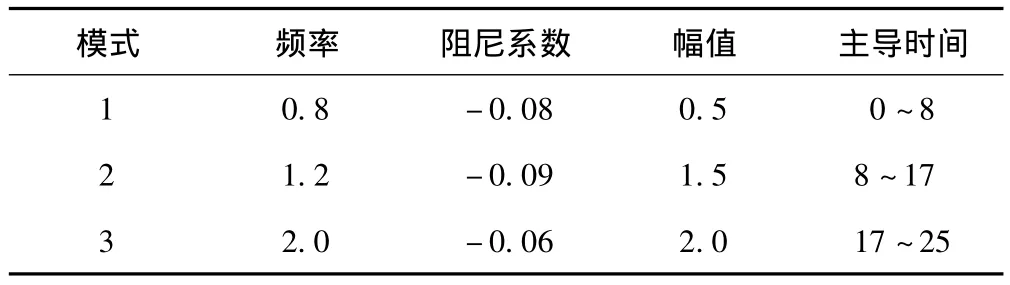
表1 信号的组成分量

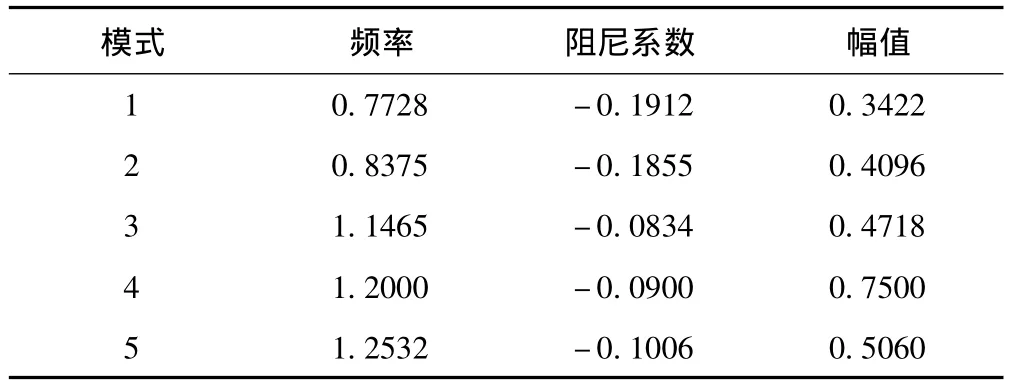
表2 prony算法的识别结果

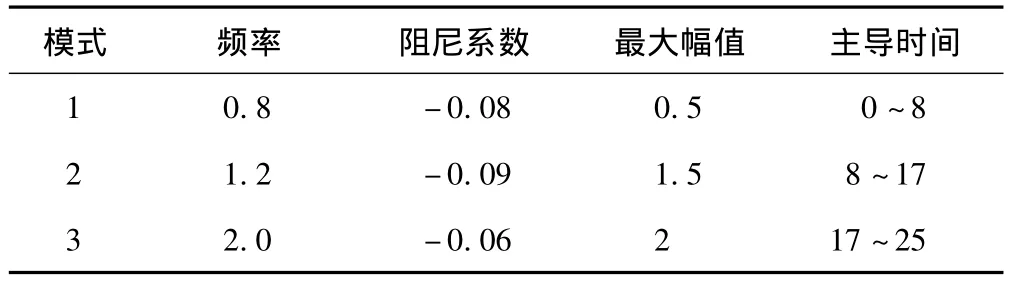
表3 滑窗prony算法的识别结果

表2中仅列出prony识别结果中幅值较大的几个模式，由表2可知在对信号的时变特性没有足够了解的前提下，Prony算法分析的误差较大，无法得出精确的模式特征参数，但滑窗prony算法可以进行时变特性信号的识别分析，由表3数据分析可知，滑窗prony算法对振荡模式识别结果较精确。

4.2 算例2

为模拟振荡模式相互作用复合新的振荡模式的现象［2］，构造信号如下:

表4 信号的组成分量

由表4可知:在8s时，模式1和模式2相互作用，复合出一个超低频振荡模式，且该模式被激励的程度较强，成为系统的主要模式。

表5和表6分别为prony和滑动prony算法识别结果。

表5 prony算法的识别结果

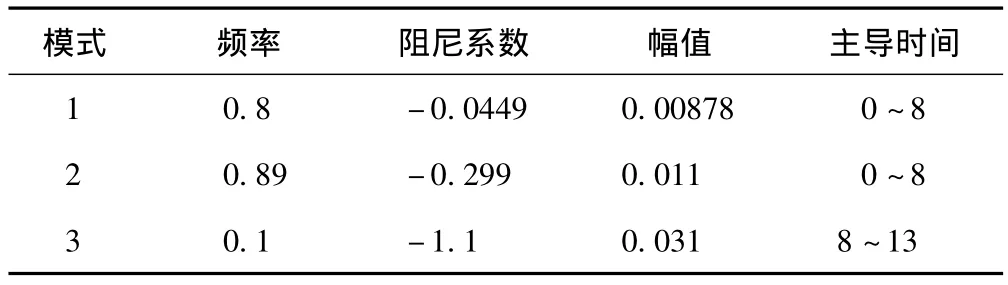
表6 滑窗prony算法的识别结果

表5中仅列出prony识别结果中幅值较大的几个模式，在8s后因模式1和模式2相互作用复合产生的主导振荡模式模式3，prony无法将其识别出，但滑窗prony算法可以识别出模式的变化，较为准确的识别出相互作用产生的超低频振荡模式。

5 结论

Prony算法能够直接计算出信号的幅值、频率、衰减因子及相位，为电力系统低频振荡主导模式识别提供了良好的条件。针对传统的prony算法只能采取局部信号进行分析，而且抗噪性能较差的缺点，而实际电力系统振荡模式具有时变性和多模式的特点，本文提出了滑窗prony的时变特性方法。理论分析和算例表明:该算法可以分析处理平稳信号，反映振荡的时变特性，可以更好地描述信号的变化规律，揭示传统分析方法(如Prony算法)难以描述的振荡特性，更有利于机理的解释。

［1］ 郝思鹏，袁越，陈小虎，等．用窗口傅里叶脊提取时变振荡信息［J］．电力自动化设备，2011，31(5):58－62．

［2］ 邓集祥，涂进，陈武晖．大干扰下主导低频振荡模式的鉴别［J］．中国电机工程学报，2007，31(7):36 －41．

［3］ 李天云，高磊，赵妍．基于HHT的电力系统低频振荡分析［J］．中国电机工程学报，2006，26(14):24．29．

［4］ 倪以信，陈寿孙，张宝霖．动态电力系统的理论和分析［M］．北京:清华大学出版社，2002．

［5］ 鞠平，谢欢，孟远景，等．基于广域测量信息在线辨识低频振荡［J］．中国电机工程学报，2005，25(22):56 －60．

［6］ 徐东杰，贺仁睦，高海龙．基于迭代Prony算法的传递函数辨识［J］．中国电机工程学报，2004，24(6):40 －43．

［7］ T．Hiyama，N．Suzuki，T．Funakoshi．On-line Identification fo Power System Oscillation Modes By Using Real Time FFT［C］．IEEE PESWinter Meeting，Singapore，2000．

［8］ 张鹏飞，薛禹胜，张启平．电力系统时变振荡特性的小波脊分析［J］．电力系统自动化，2004，28(16):32 －35，66．

［9］ 董航，刘涤尘，邹江峰．基于Prony算法的电力系统低频振荡分 析［J］．高电压技术，2006，32(6):97 －100．

［10］ 王铁强．电力系统低频振荡共振机理的研究［D］．北 京:华北电力大学，2001．

［11］ 肖晋宇，谢小荣，胡志祥，等．电力系统低频振荡在线辨识的改进Prony算法［J］．清华大学学报(自然科学版)，2004，44(7):883 －887．

［12］ 李大虎，曹一家．基于模糊滤波和Prony算法的低频振荡模式在线辨识方法［J］．电力系统自动化，2007，31(1):14 －19．

［13］ Z．Leonowicz，T．Lobos，and J．Rezmer．Advanced spectrum estimation method for signal analysis in power electronics［J］．IEEE Tran．Industrial Electronics．2003，50(3):514 －519．

［14］ 王洋，王宁会．基于Prony算法的静电除尘器放电信号分析［J］．中国电机工程学报，2003，23(1):141 －144．

［15］ 熊俊杰，邢卫荣，万秋兰．Prony算法的低频振荡主导模式识别［J］．东南大学学报(自然科学版)，2008，38(1):64 －68．

［16］ 丁蓝，薛安成，李金，等．基于窗口滑动改进Prony算法的电力系统低频振荡识别［J］．电力系统自动化，2010，34(22):24 －28．

The Analysical M ethod of Time-varying Oscillation Characteristic of Silding W indow Porny Algorthm

YANG Li-bo1，YANG Fang2
(1．Hunan Grid Engineering Company，Hengyang，421002，China;2．Qingyuan Power Supply Bureau，Qingyuan，511500，China)

Prony algorithm can extractoscillation frequency and damping of the smooth signal，but can notaccurately reflect the oscillation characteristics of the time-varying signal．The real low-frequency oscillations usually havemulti-mode time-varying characteristics and theremay exist the compositemode．The time-varying oscillation signal with the sliding window Prony algorithm analysis is proposed．Sliding thewindow to observe the time-varying characteristics of the oscillation signal．Calculations have proved that the sliding window Prony algorithm can better analyze the time-varying characteristics of the low frequency oscillationmode，which ismore suitable for the oscillation information analysis of the actual power system．

power system;low frequency oscillation;sliding window;Prony

TM711

B

1004－289X(2013)03－0054－04

2013－03－20

杨利波(1982－)男，助理工程师，主要研究方向为电力运行;

杨芳(1986－)男，硕士研究生，主要研究方向为电力系统稳定与控制。