接近负荷极限的快速在线估算法

廖青华，张锐

(河南机电高等专科学校电气工程系，河南 新乡 453000)

接近负荷极限的快速在线估算法

廖青华，张锐

(河南机电高等专科学校电气工程系，河南 新乡 453000)

接近负荷极限或PV曲线的鼻尖点以及电压不稳定已成为了现代电力系统的主要关注点之一，近年来，在线估算电压稳定极限吸引了许多电力研究者的关注。介绍了一种简单的在线估算接近负荷极限的局部指标，只需要使用两个连续的局部测量标量。该指标是在负荷视在功率在负荷极限点不变的前提下推导出来的，应用该方法可以实现采用数字继电器实施局部控制来阻止电压不稳定，以及在系统控制中心实施全系统的调整分析与控制措施。对IEEE 30节点系统进行了仿真计算，仿真结果验证了所提方法的可行性和有效性。

在线估算;负荷极限;电压稳定极限;PV曲线;局部指标

1 引言

经济与环境的发展制约使得电力系统运行越来越接近于电压稳定极限，因此，电压不稳定已成为引起现代电力系统大面积停电事故的最常见原因之一。由于系统经常运行在接近电压稳定极限的点，在线监测其稳定状态就显得非常必要。接近PV曲线的鼻尖点或负荷极限是电压稳定极限的最通用评估标准。国内外许多学者提出了各种不同的方法用于估算系统运行点接近负荷极限的程度，即电压稳定安全指标［1］。这些方法中的大多数是研究潮流问题以及潮流雅可比矩阵，然而，在实际电力系统中，系统以及雅可比矩阵的规模太大，以致这些方法计算起来耗时太长，而且可能不适合在线分析。文献［2］介绍了一种应用电力系统仿真软件求解大规模电网最大负荷极限点的方法，全面地考虑了对负荷极限求解有影响的因素，但算法实现起来较麻烦，而且不是采用局部测量的算法。

近年来，也有学者提出采用局部测量算法来计算负荷极限［3－5］。这些方法足够快，且适合在线分析。然而，这些方法仍不成熟，有些方法并不能在所有条件下都适合。文献［3］和［4］介绍了一种引人关注的估算运行点与负荷极限之间接近程度的指标，尽管在负荷极限点电压和电流是变化的，该指标是在负荷视在功率在负荷极限点不变的基础上推导出来的，称作SDC，其定义如下:

该指标应用两个连续的局部测量电压相量和电流相量，除了需要测量相量的仪器外，这种方法的另一个问题是，在稳定区和不稳定区，分别对应于PV曲线的上半支与下半支，指标值都是正的。因此，如果在被监测母线附近发生一个大的扰动，导致运行点从稳定区跳变到不稳定区，且维持电压水平合理，该指标就不能辨别出运行点已进入了不稳定区。

本文应用与SDC指标相同的基本概念，介绍一种新的方法，估算运行点与负荷极限之间接近程度的指标，不存在上述问题。

2 算法原理

任一电力系统，从任意一个负荷节点看进去的戴维南等值模型如图1所示。

图1 从某一负荷节点看进去的电力系统戴维南等值模型

若将负荷视在功率对负荷导纳的模求导，再除以负荷电压幅值的平方得到:

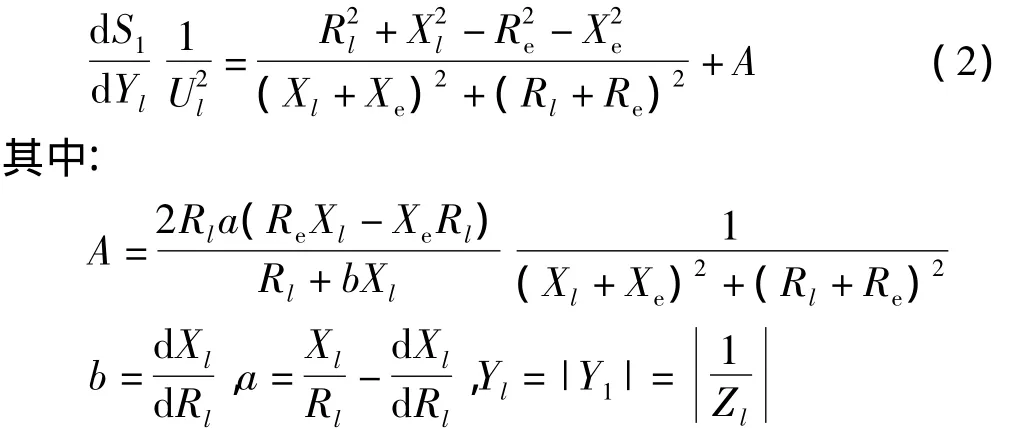
当负荷功率因素恒定时，变量A等于零。在一个实际电力系统中，在负荷自然变化期间，功率因数有细微的变动。然而，即使在功率因数变化非常大的情况下，变量A也足够小，可以忽略不计。因此，可以不考虑负荷功率因数的变化，认为负荷极限就是(Zl/Ze)等于1的点，同时，在采用间隔中，被测样本间的差别足够小，dSl/dYl可以用 ΔSl/ΔYl取代，因此，式(2)可以简化为:

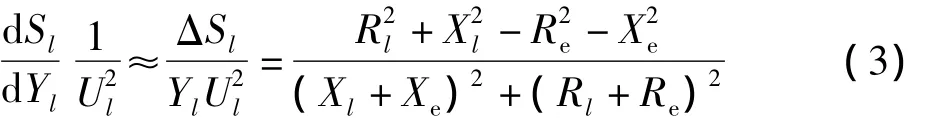
根据以上等式，介绍一种改进的负荷极限指标如下:

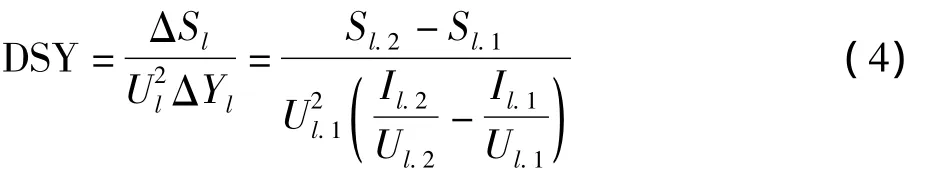
我们之所以称其为DSY指标，源于求取负荷视在功率(S)对它的导纳(Y)的导数(D)。由于S=UI，要计算该指标，只需要Il与Ul两个连续的测量值，用下标1和2表示，通过局部测量就可得到现成的数据，而并不需要测量相量。

从式(3)可以明显看出，介绍的该指标值在负荷极限以上的区域(稳定区)是正的，在负荷极限以下的区域(不稳定区)是负的，在负荷极限(临界点)等于零。对一个如图1所示的简单系统，给出以下参数值:Ee=1，Re=0.004，Xe=0.03，cosφ =0.95，将提出的新指标与SDC指标同时描述在图2中，显然，本文所提指标与其他指标相比，体现出的特征更具有指导意义。

图2 如图1所示等值系统的SDC与DSY指标曲线

3 算例及分析

用本文方法对IEEE30节点系统进行了仿真计算，本次仿真考虑两种不同的负荷增长情况，第一种情况是，负荷增大且保持功率因数保持不变;第二种情况是，负荷增大，功率因数在很大范围内大幅度变化，以至于最危险节点(其指标值最低)的功率因数从最初运行点的0.94下降到负荷极限点的0.55。在两种情况下，所有PQ节点的负荷都是按按功率因数同比例增长的，同时，发电机的无功功率都在允许范围内，发电机的有功出力是根据它们的额定功率安排的。

在两种情况下，最危险节点都是19节点。图3描述了两种情况下最危险节点的指标值变化情况，第二种情况下变量A的变化情况也体现在图3中。显然，即使在负荷功率因数大幅度变化情况下，变量A也足够小，可以忽略，本文提出的指标有效，在负荷极限指标值变为零。图3中出现的指标值突变是由于发电机节点从PV节点向PQ节点转换。仿真结果表明，DSY最接近于零与系统最接近负荷极限以及潮流发散的特征是一致的。

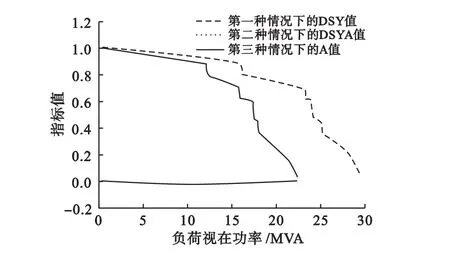
图3 IEEE30节点系统最危险节点的DSY指标值变化情况

3 结论

文章介绍了一种在线估算最接近负荷极限的新指标，基于负荷视在功率在负荷极限不变的事实，应用两个连续局部测量标量(电压、电流有效值)。该指标与以前提出的基于相同概念的SDC指标相比，有两个主要优势:

(1)该指标不需要相量测量数据，因此可以应用于几乎所有变电站。

(2)该指标值在稳定区和不稳定区的正负符号不同，这样就很容易发现由于被监测母线附近的某种扰动引起运行点从稳定区转移到不稳定区的情况。

［1］ 程浩忠，吴浩．电力系统无功与电压稳定性［M］．北京:中国电力出版社，2004．

［2］ 熊宁，程浩忠，胡泽春，等．基于PSS/E的最大负荷极限的求解方法［J］．电力系统保护与可控制，2008，36(20):1 －4．

［3］ G．Verbic，F．Gubina．A new concept of voltage-collapse protection based on local phasors［J］．IEEE Trans on Power Systems，2004，19(2):567－581．

［4］ G．Verbic，F．Gubina．Fast voltage-collapse line-protection algorithm based on local phasors［J］．IEEE Trans on Power Systems，2003，15(4):482－486．

［5］ K．Vu，M．Begovic，D．Novosel，M．M．Saha．Use of localmeasurements to estimate voltage-stabilitymargin［J］．IEEE Trans on Power Systems，1999，14(3):1029－1035．

A Fast Online Estimated M ethod of Approuching Load Lim it

LIAO Qing-hua，ZHANG Rui
(Dept of Electrical Engineering，Henan Mechanical and Electrical Engineering College，Xinxiang 453000，China)

Approaching load limit or nasal tip point of PV curves，and voltage instability is one of the major focus of modern power systems，Online estimation of voltage stability limithas attracted the attention ofmany power researchers in recent years．A simple local index for online estimation of Approaching load limit is introduced，which needs only two consecutive local scalarmeasurement．This index is achieved based on the fact that the load apparent power is constantat load limit．The index is suitable in digital relays for implementation of local control to prevent voltage instability，and in the system control center，the adjustment analysis of the whole system and controlmeasures．Simulation results on the IEEE 30-bus test system show the feasibility and effectiveness of the proposed method．

online estimation;load limit;voltage stability limit;PV curve;local index

TM71

B

1004－289X(2013)03－0035－03

2013－03－28

廖青华(1978－)，女，湖南新化人，硕士，讲师，研究方向:电力系统分析与计算;

张锐(1983－)，女，河南西平人，硕士，助教，研究方向:发电厂设备控制与运行维护。