非局部变分修复法去除高密度椒盐噪声

杨文波，马天玮，刘 剑

（1.中国科学院长春光学精密机械与物理研究所航空光学成像与测量中国科学院重点实验室，吉林长春130033；2.中国科学院大学，北京100049）

非局部变分修复法去除高密度椒盐噪声

杨文波1，2*，马天玮1，刘 剑1

（1.中国科学院长春光学精密机械与物理研究所航空光学成像与测量中国科学院重点实验室，吉林长春130033；2.中国科学院大学，北京100049）

分析了中值滤波及其改进型算法在处理高密度椒盐噪声时效果不理想的原因，采用变分修复方法来去除高密度椒盐噪声，基于现有的全变差修复模型提出了非局部全变差修复模型。该模型利用椒盐噪声特点（均匀分布、灰度值为0或255），将噪声点看成是图像中遗失或是破损的点，首先在图像中寻找与噪声点邻域相似的区域，将相似区域的中心像素作为噪声点新的邻域然后对其插值，把图像降噪问题转化为图像修复问题，从而达到去除高密度噪声的目的。实验结果表明：该模型对噪声密度为90%的彩色和灰度图像去噪后，其峰值信噪比为22.85和28.77，在客观评价标准方面优于中值滤波及其改进型算法。该模型能有效去除高密度下的椒盐噪声并较好地恢复图像细节，为图像去除高密度噪声提供了一种新的途径。

图像去噪；图像修复；椒盐噪声；中值滤波；非局部变分修复

1 引 言

椒盐噪声是一类典型的非线性噪声，也是被研究最多的一类噪声。中值滤波（Standard Median Filter，SMF）则是一种方便且有效的非线性去除椒盐噪声的方法，由于其简单、易于实现并具有一定的图像细节保留能力，一直都是人们关注的热点。然而这一算法最大的缺点就是对所有的像素均采用统一的处理方法，因而导致图像细节损失。

为了进一步提高滤波效果，近年来学者们已提出了很多改进型中值滤波算法。如文献［1］提出了一种加权中值滤波（Weighted Median Filter，WMF）算法，它可粗略估计噪声的污染率，然后自动调整中心像素的权值，从而控制新的滤波器对噪声图像进行平滑。文献［2］、［3］提出了开关滤波（Switching Median Filter）算法，其思想是在滤波之前把受污染与未受污染像素区分出来，然后用中心像素值替换受污染的像素，同时不改变未受污染的像素值；但随着噪声密度增加，用于替换的中心像素值也可能受到污染，失去抑制噪声的能力。为了克服以上缺点，文献［4］提出一种自适应中值滤波算法（Adaptive Median Filter，AMF），首先将图像中噪声点检测出来，然后根据一定规则调整窗口大小来相对地降低噪声密度，以确保中值是未受噪声污染的像素点；它的主要缺点是调整到“大窗口”滤波将非常耗时。与AMF方法不同的是文献［5］提出的基于决策的滤波方法（Decision-Based Algorithm，DBA），该方法在噪声密度较高条件下，中心像素值可能受到污染，这时可用其邻域像素值作为中心像素值进行滤波，这是因为中心值与其邻域像素值具有较高的相关性，这种高度相关性保证了滤波效果。文献［6］也提出了类似方法，利用邻域差分法判断中心像素是否受到污染，若判定该点为噪声，则将邻域像素分别赋予不同权值对该点像素重构。文献［7］则是利用模糊推理的方法恢复受到污染的中心像素值；由于其随着噪声密度的进一步增加，不仅中心像素值易受污染，而且其邻域也易受到污染，文献［8］提出了基于鲁棒估计算法（Robust Estimation Algorithm，REA），该算法应用鲁棒估计对整个窗口内像素值进行检测，找到未受污染最优像素值作为替换值进行滤波；但当噪声密度增加到一定程度时，文献［8］易丢失图像的特征细节，使图像模糊。考虑以上这些改进型中值滤波算法在高密度噪声条件下，滤波效果不理想，没有克服对噪声强度的敏感性，应用具有很大的局限性，本文提出采用变分修复方法来去除高密度椒盐噪声，该方法在客观评价标准方面优于中值滤波及其改进型算法。

2 高密度噪声下的中值滤波失效

设椒盐噪声的理论模型为：

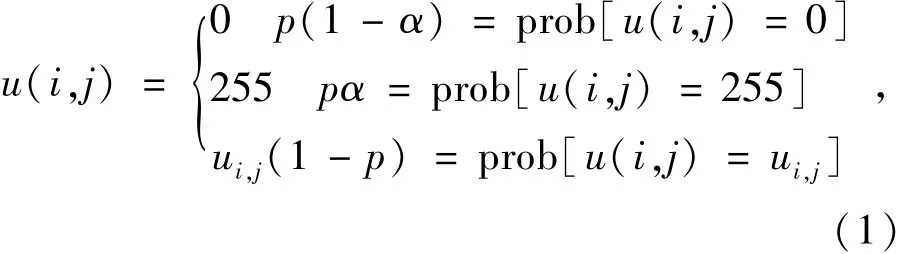
式中，p为椒盐噪声的空间密度；而α则表示椒盐混合中“盐”的百分比；对于含有椒盐噪声的图像u，假设其灰度值在a和b之间，为方便起见，认为a=0对应于暗色或是“黑椒”，而b=255对应于亮色或是“盐”。

设m和n为两个固定大小的尺寸参数，则定义移动窗口为：

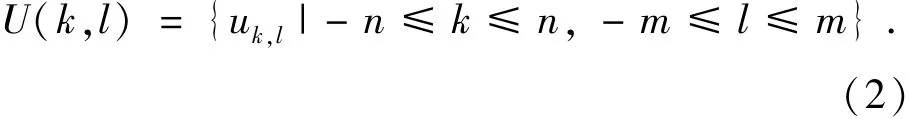
即在每个窗口U（k，l）内有N=（2n+1）×（2m+1）个样本，其中有Np（1-α）个“黑椒”样本，Npα个“盐”样本，以及N（1-p）个ui，j样本。

定义中值估计为：

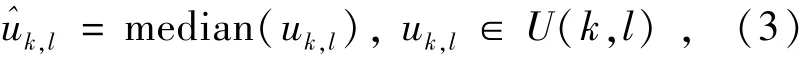
若有

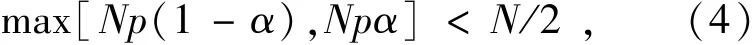
成立，则中值估计uˆk，l总是窗口内的U（k，l）中一个值，并且中值估计uˆk，l与其理想值u0k，l是非常接近的。注意到当p＜50%，即椒盐噪声的空间密度较低时，式（4）对任意均α成立。

为了定量分析在式（2）条件下，中值估计uˆk，l总能落在窗口U（k，l）内，引入下述公式，对于一个任意大小的窗口N，有［9］：

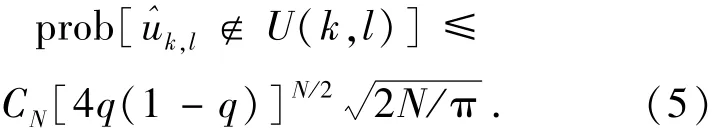
式中，q=p max（α，1-α）≤1/2，CN趋近于常数1，在应用中可令CN=1。应用该公式可定量估算出中值估计k，l落在窗口U（k，l）内的概率。考虑当p=20%及α=1/2时的低密度椒盐噪声情况时，假设使用一个7×7的移动窗口，则N=49且式

由此可见，上述两种情况都是小概率事件，基本不可能发生，这是因为式（5）是指数因子占优势，即

式（5）同时还指出了当空间密度较大时中值滤波方法存在的潜在问题。在这种情况下，p→1，q= p/2≅1/2，因为4q（1-q）≅4×1/2×1/2=1，指数因子不再占优势，prob（k，l∉U（k，l））概率增大，使中值滤波方法失效。因此，去除高密度椒盐噪声需要中值滤波以外的新方法。

3 变分修复法去除高密度椒盐噪声

3.1 全变差（Total Variation，TV）修复模型去噪

当噪声密度较高，如p≥50%时，需要使用图像修复技术进行复原。这是因为这时可以将椒盐噪声看成是图像中遗失或是破损的部分，利用未被损坏的图像信息，按照一定的规则对其填补，使修复后的图像接近原图视觉效果。

Chan和Shen在文献［10］中提出了一种变分修复模型，即全变差修复模型，它所对应的时间演化方程为：

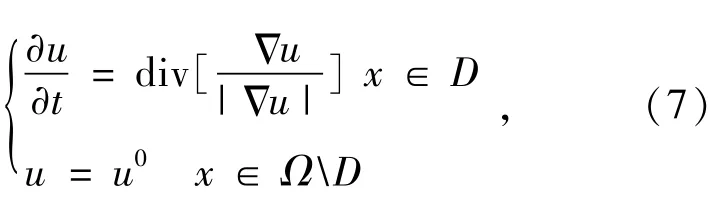
式中，D=｛x∈Ω|u（i，j）=0‖u（i，j）=255｝为待修复区域。由式（1）可知，椒盐噪声只会污染图像中的部分像素点，而其它像素的灰度值则保持不变；假设噪声污染前的图像是自然变化的灰度图像，如果图像中像素的值为0或255，可将该点认为是噪声污染点，即需要修复的点。但也存在着像素值为0或255可能是有效数据的情况，在这种情况下，仍可将该点作为噪声点。这是因为在自然变化图像中，TV模型依靠该点邻域信息对其进行插值迭代，最终可使该点接近或达到0或255，避免了图像的失真；同时式（7）实质上是一个各向异性扩散方程，它仅在修复区域边缘切线方向扩散，保留了图像的细节。但是它也有十分明显的缺点：TV模型仅仅是一个临近的线性插值，图像的修复区域完全被它临近区域决定，扩散过程完全依赖于图像的局部特性。考虑到在高密度噪声条件下，在接近边缘部分或梯度较大的地方，由于噪声干扰，使得各向异性扩散变为各向同性扩散，平滑了图像的边缘，损失了图像的细节，修复的图像会产生虚假的现象。为了克服这一缺点，应当采用非局部算子重新设计TV修复模型，使得扩散过程不依赖于图像的局部特性，称该模型为非局部全变差（Non-Local Total Variation，NLTV）修复模型。

3.2 NL-TV修复模型去噪

采用文献［11］提供非局部算子设计NL-TV模型。定义图像函数u（x）在像素x关于像素y的非局部梯度向量Δuw（x，y）及其模分别为：

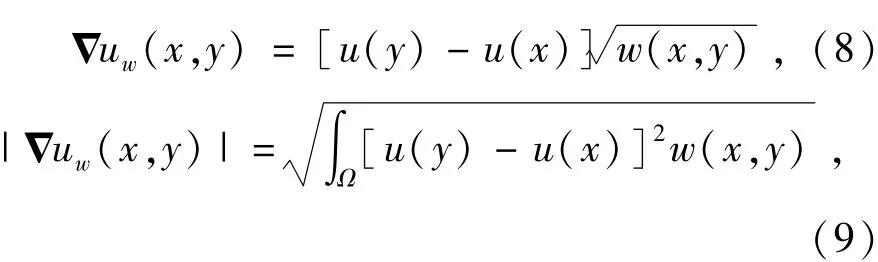
式中，w（x，y）是像素x与像素y之间的权重因子，权重因子w（x，y）的取值主要依靠像素x与像素y的之间的相似性，且权重因子满足0≤w（x，y）≤1，w（x，y）=w（y，x）。衡量像素x与像素y之间的相似性，需衡量它们邻域间的相似性，这主要是由于自然图像的高度冗余性，即在同一幅图像上的一个小区域存在着与其相似的多个小区域。可用下式衡量邻域间的相似性，即区域间距离［12］：

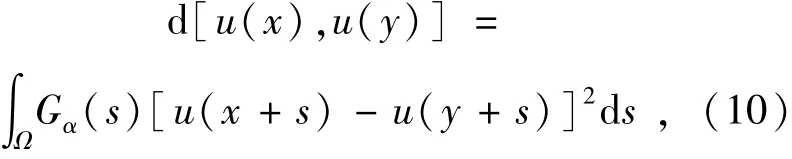
式中，Gα（s）是方差为α的高斯函数。如果像素间有相似邻域，则它们的权重因子w（x，y）较大，如图1所示，q1和q2具有较大权重，因为它们有相似的邻域，w（p，q3）重较小，因为它们邻域间灰度值相差较大。

图1 权重因子示意图Fig.1 Scheme of the weighted factor

为了计算方便，可将权重因子w（x，y）定义为［13］：

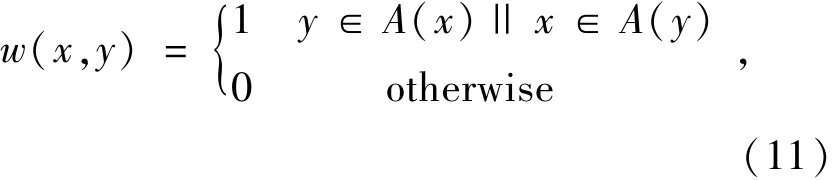
式中，A（x）是图像中与像素x最相似点的集合，根据式（11），A（x）可被定义为：

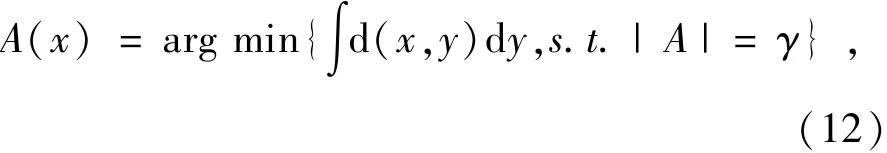
式中，γ是像素点集合的元素个数。

根据文献［10］定义向量Δuw的非局部散度公式为：

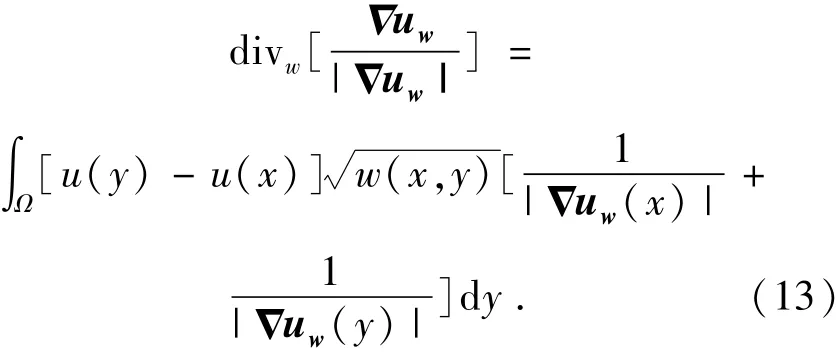
基于以上非局部算子以及TV修复模型，给出NL-TV修复模型时间演化方程：

3.3 NL-TV模型的离散化

对于NL-TV修复模型（14）给出如下离散化差分迭代公式：

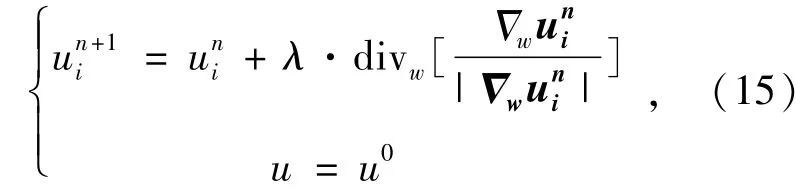
式中，λ是时间步长。对于空间差分算子采用如下离散化公式：

式中，wi，j是w（x，y）的离散值，Ni=｛j:wi，j＞0｝。

为了更好地理解TV模型和NL-TV模型，下面比较两种模型的离散化公式，TV模型可简化如下形式：

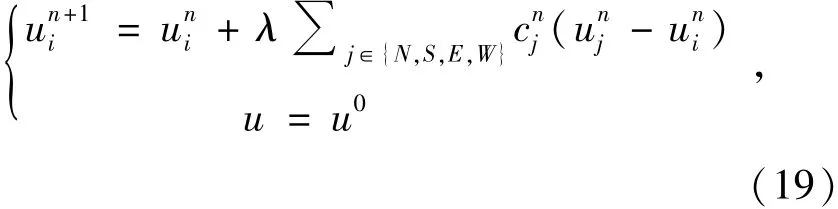
式中，N，S，E，W是像素i的垂直和水平方向的四邻域；同样NL-TV模型也可以简化为：

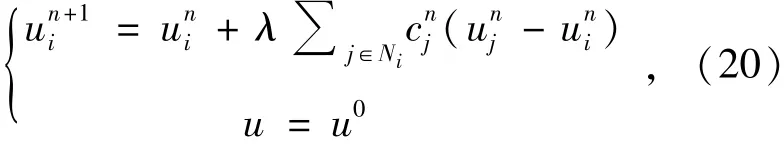
式中，Ni=｛j:wi，j＞0｝是与像素i最相似点的集合。对比式（19）和（20）可以十分明显观察出两种模型间的差异，TV模型依靠局部空间的像素信息估计缺失或受污染像素值，而NL-TV模型主要依靠全局的相似像素，保证扩散过程是各向异性。

对于权重因子w（x，y）离散化计算过程如下：为了减少计算，首先在一个固定窗口内，选取像素i的一个固定大小邻域；然后计算它对窗口内所有同等大小邻域的距离（dα）i，j，选取k个距离最小的邻域；最后将这些邻域围绕的像素j赋值为1，其余的赋值为0。

4 实验结果

本节采用实验验证本模型的有效性。首先对图2大小为256×256彩色图像pepper添加60%～90%高密度椒盐噪声，然后用TV模型和NLTV模型去噪。实验中选择固定窗口大小为21× 21，邻域像素块大小为5×5，时间步长λ=10，高斯函数的方差α=5。

通过图2的对比效果可以看出，TV模型虽能平滑平坦区域的噪声，但是由于高密度噪声干扰，使各向异性扩散过程失效，边缘信息未受到保护，图像的细节信息损失严重，且随着噪声增加，这一现象越发明显；而NL-TV模型却具有很好的效果，在滤除噪声的同时，对细节信息的保护也做得很好。

图2 TV和NL-TV对pepper图像在不同密度噪声下去噪效果Fig.2 Restoration results of TV and NL-TV for pepper image at different noise densities

对滤波效果的评价除了主观评价外，还需结合一种客观的评价方法。本文采用峰值信噪比（Peak Signal Noise Ratio，PSNR），均方误差（Mean Square Error，MSE）和平均绝对误差（Mean Absolute Error，MAE）作为评价标准。它们的定义如下：

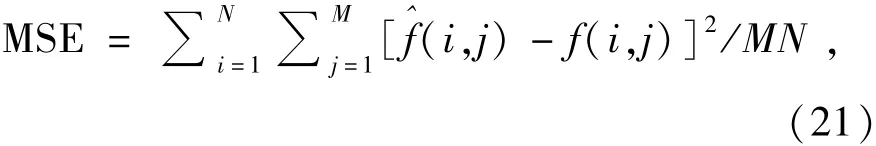
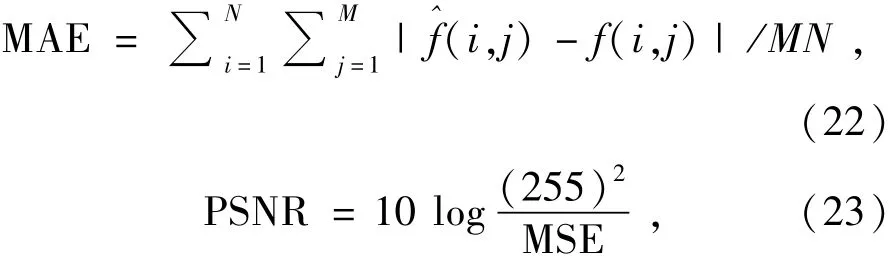
从图2对比可知，在各噪声密度下NL-TV的PSNR均大于TV的PSNR值，平均超出4.36 dB，这也表明NL-TV模型去噪性能优于TV模型。

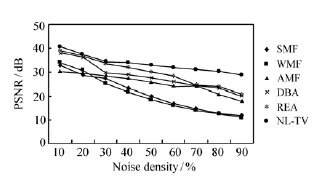
图3 各种方法的PSNR值对比图Fig.3 Comparison of PSNRswith differentmethods

图4 各种方法的MSE值对比图Fig.4 Comparison of MSEs with differentmethods

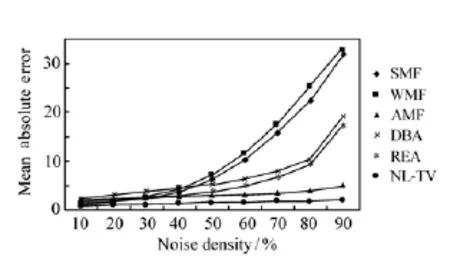
图5 各种方法的MAE值对比图Fig.5 Comparison of MAEswith differentmethods

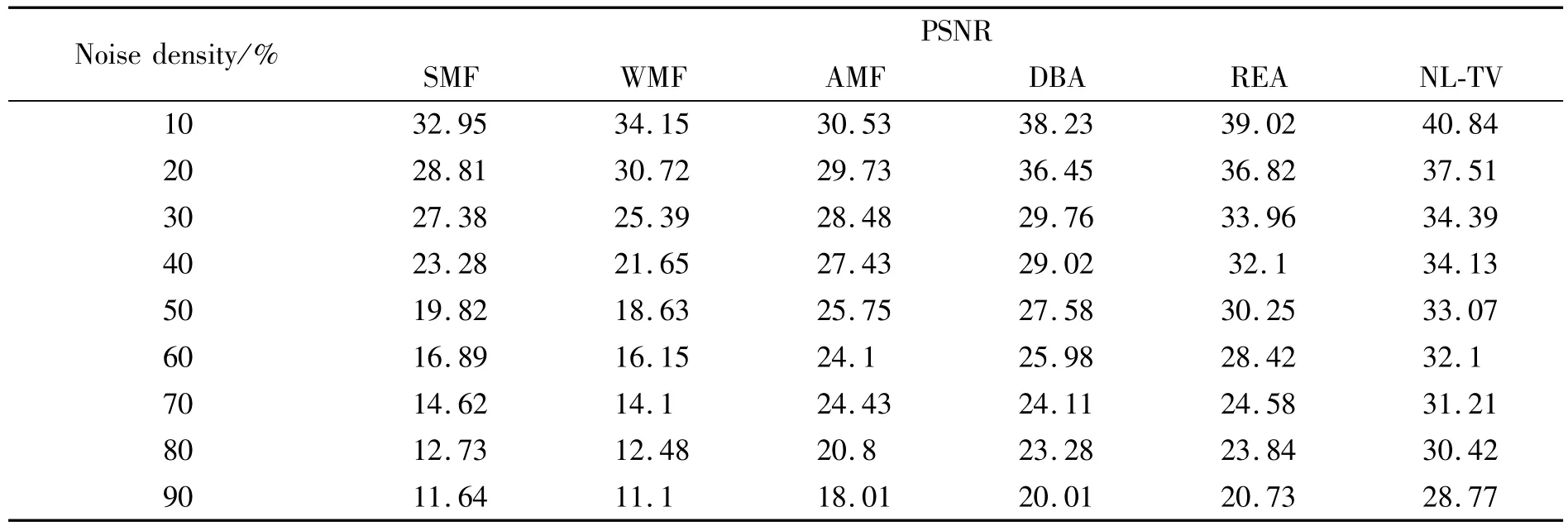
表1 各种方法的PSNR值比较Tab.1 Comparative results of variousmethods in terms of PSNRs

文献［8］比较了SMF、WMF、AMF、DBA以及REA算法的去噪性能，因此本文也选取大小为256×256的8位灰度图像Lena，分别添加10%～90%的椒盐噪声，以PSNR、MSE及MAE标准验证算法性能，表1～3和图3～5是实验结果，图6（a）～（h）是在噪声密度60%的条件下，各种算法的去噪效果。由实验结果可以看出，在噪声水平低于30%时，各种算法的客观评价标准相差不大，这意味着它们都能够有效地去除噪声；当噪声水平高于50%时，SMF、WMF和AMF算法性能急剧下降，表现为客观评价标准超出了正常值范围；虽然DBA和REA算法也能去除较高密度的噪声，但随着噪声密度的进一步增加，DBA和REA算法性能也在逐步失效。从图6可以看出，当噪声水平达到60%时，DBA和REA会产生拖尾现象和边缘模糊现象，不能恢复图像的细节，而

NL-TV模型去除椒盐噪声时，视觉效果明显优于其它几种方法。实验结果表明，无论是去除低密度还是高密度的椒盐噪声，NL-TV模型的客观评价标准全面优于中值滤波及其改进型算法。

表2 各种方法的MSE值比较Tab.2 Comparative results w ith variousmethods in terms of MSEs

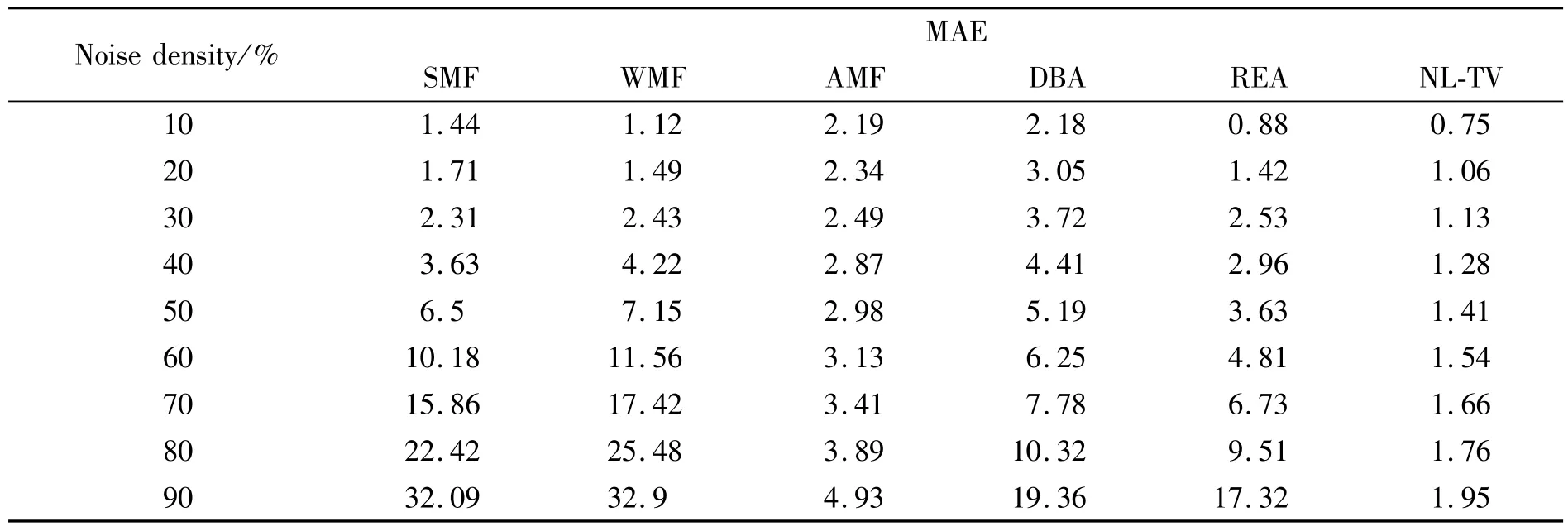
表3 各种方法的MAE值比较Tab.3 Comparative resultsw ith variousmethods in terms of MAEs

图6 各种方法对噪声密度为60%的Lena图像去噪效果Fig.6 Restoration results with variousmethods for Lena image with 60%salt-and-pepper noise

5 结 论

椒盐噪声在工程中比较常见，主要因信号在电路传输中发生错误而产生，其危害效果很严重，尤其是红外相机的图像中经常伴随着较高密度椒盐噪声，对后期图像处理产生较大影响。SMF及其改进型算法对于去除低密度椒盐噪声是一个简单且有效的方法。但当噪声密度较高时就需要采用除了SMF以外的新方法，如变分修复的方法。

本文提出了一种NL-TV修复模型用于去除高密度椒盐噪声。该模型与SMF及其改进型有本质区别：首先它将噪声点看成是图像中遗失或破损的点，把图像降噪问题转化为图像修复问题；其次它不需检测噪声点，直接将灰度值为0或255像素认为是噪声，在图像中寻找与噪声点邻域相似的区域，将相似区域的中心像素作为噪声点新的邻域，然后对其插值迭代，实现噪声去除同时恢复被误认为是噪声点的有效数据。该模型与TV模型的最大不同点是：它的扩散是全局意义下的各向异性扩散，对图像细节恢复较TV模型好。基于以上原因使得该模型去噪后的图像比较真实，有较好的视觉效果。

仿真实验结果表明：该模型对噪声密度为90%的彩色和灰度图像去噪后，其PSNR值分别为22.85和28.77，各方面优于SMF及其改进型算法，为图像降噪提供了新的途径。

［1］ ZHANG X，XIONG Y.Impulse noiseremoval using directional difference based noise detector and adaptiveweightedmean filter［J］.IEEE Signal Processing Lett.，2009，16（4）：295-298.

［2］ IBRAHIM H，KONG N.Simple adaptivemedian filter for the removal of impulse noise from highly corrupted images［J］. IEEE Trans.Consumer Electronics，2008，54（4）：1920-1927.

［3］ AKKOUL S，LECONGE R，HARBA R.A new adaptive switchingmedian filter［J］.Signal Proc.Lett.，2010：587-590.

［4］ CHAN R H，HO CW，NIKOLOVA M.Salt-and-pepper noise removal bymedian-type noise detectors and detail-preserving regularization［J］.IEEE Trans.Image Process，2005，14（10）：1479-1485.

［5］ SRINIVASAN K S，EBENEZER D.A new fast and efficient decision-based algorithm for removal of high-density impulse noises［J］.IEEE Signal Proc.Lett.，2007，14（3）：189-192.

［6］ 王明佳，张旭光，韩广良，等.自适应权值滤波消除图像椒盐噪声的方法［J］.光学精密工程，2007，15（5）：779-783. WANG M J，ZHANGX G，HANG L，etal..Elimination of impulse noise by auto-adapted weight filter［J］.Opt.Precision Eng.，2007，15（5）：779-783.（in Chinese）

［7］ TOH K K V，ISA N A M.Noise adaptive fuzzy switchingmedian filter for salt-and-pepper noise reduction［J］.IEEE Signal Proc.Lett.，2010，17（3）：281-284.

［8］ VIJAYKUMAR V R，VANATHIPT，EBENEZER D.High density impulse noise removal using robustestimation based filter［J］.IAENG International J.Computer Science，2008，35（3）：140-148.

［9］ CHAN T F，SHEN JH.图像处理与分析-变分，PDE，小波及随机方法［M］.陈文斌、程晋译.北京：科学出版社，2011. CHAN T F，SHEN JH.Image Processing and Analysis：Variational，PDE，Wavelet，and Stochastic Methods［M］.CHEN W B，CHENG J translate.Beijing：Science Press，2011.（in Chinese）

［10］ CHAN T F，SHEN JH.Nontexture inpainting by curvature driven diffusions（CDD）［J］.Visual Comm.Image Rep.，2001，12：436-449.

［11］ GILBOA G，OSHER S.Nonlocaloperatorswith applications to image processing［J］.SIAM MultiscaleModeling and Simulation，2008，7（3）：1005-1028.

［12］ BUADESA，COLL B，MOREL JM.On image denoisingmethods［J］.SIAM Multiscale Modeling and Simulation，2005，4（2）：490-530.

［13］ BUADESA，COLL B，MOREL JM.Neighborhood filters and PDE′s［J］.NumerischeMathematik，2006，105（10）：1-34.

作者简介：

杨文波（1980—），男，吉林省吉林市人，博士研究生，2010年于长春理工大学获得硕士学位，主要从事超分辨率重构、图像复原方面的研究。E-mail：ywbcust @sina.com

马天玮（1978—），男，吉林白山人，副研究员，主要从事图像处理及嵌入式系统应用方面的研究。E-mail：maxpony@ 263.net

刘 剑（1973—），男，吉林长春人，高级工程师，主要从事图像处理方面的研究。E-mail：Ky1_liujian@sina.com

Elim ination of impulse noise by non-local variation inpaintingmethod

YANGWen-bo1，2*，MA Tian-wei1，LIU Jian1
（1.Key Laboratory of Airborne Optical Imaging and Measurement，Changchun Institute of Optics，Fine Mechanics and Physics，Chinese Academy of Sciences，Changchun 130033，China；2.University of Chinese Academy of Sciences，Beijing 100049，China）
*Corresponding author，E-mail：ywbcust@sina.com

The reasons of ineffectiveness of median filtering and its improved algorithm for eliminating the high-density salt-and-pepper noise are analyzed.A variational inpainting method is adopted to remove the high-density salt-and-pepper noise，and a inpaintingmodel of Non-local Total Variation（NL-TV）based on the existingmodel of Total Variation（TV）is proposed in this article.In the NL-TVmodel based on the characteristics of salt-and-pepper noise（uniform distribution and the gray value of0 or 255），we view the noise points as the lostor damaged points of an image to find the districts similar to the neighborhoods of noise points in an image，and then interpolate the noise points by taking the central pixel in a similar district as a new neighborhood of noise points.By thismethod，we transform the problem of image denoising into a problem of image restoration to remove the high-density noise.The experimental results show that the Peak Signal to Noise Ratios（PSNRs）are 22.85 and 28.77 after removing the noise for a color and gray-scale imagewith 90%of noise density，which is better than the results obtained by median filter and its improved algorithm in terms of theobjective evaluation criteria.Using this model，we can effectively remove the high-density salt-and-pepper noise and restore the image details better，which provides a new approach to remove the high-density noise.

image denoising；image inpainting；salt and pepper noise；median filtering；non-local variational inpainting

TP391.4

A

10.3788/CO.20130606.0876

1674-2915（2013）06-0876-09

2013-09-12；

2013-10-15

中国科学院航空光学成像与测量重点实验室开放基金资助项目（No.2012MS01）