基于谱间和帧内差分脉冲编码调制的超光谱图像无损压缩

2013-04-27王军

中国光学 2013年6期

关键词：算术差分光谱

王军

（中国航天科工集团第九总体设计部，湖北武汉430040）

基于谱间和帧内差分脉冲编码调制的超光谱图像无损压缩

王军

（中国航天科工集团第九总体设计部，湖北武汉430040）

以超光谱遥感图像为研究对象，分析了干涉成像光谱仪获取图像的谱间和空间相关性，提出一种三维差分脉冲编码调制（DPCM）无损压缩方案。首先进行了谱间DPCM预测；然后，对残差图像进行帧内DPCM预测；最后，对差分码流进行二值自适应算术编码。实验表明，该算法可实现无损压缩，压缩比平均可达1.662，较二维整数小波变换算法提高了15.6%，且算法复杂度较低，仅有加减和移位运算，易于硬件实现。

超光谱图像；无损压缩；谱间差分脉冲编码调制；帧内差分脉冲编码调制；二值自适应算术编码

1 引言

超光谱图像是在二维普通图像的基础上叠加了一维光谱信息，是一类三维立体图像，由于其包含上百个谱段数，因此含有巨大的信息量。相比一般图像，超光谱图像数据压缩略有不同，一是必须采用保真度高的近无损或无损压缩算法，这是因为超光谱图像通常采用航空等遥感手段获取，花费高昂，信息重要性高；二是地质资源调查等诸多领域均需要实时传输图像，所以要求压缩系统速率高、硬件实现简便。

文献［1］描述了应用小波变换的3DSPIHT和3DEZW超光谱图像无损压缩算法。3DSPIHT算法首先通过K-L变换消除谱段之间的相关性，然后应用帧内小波变换形成三维的分级树结构，最后对其进行SPIHT编码。作为比较应用JPEG2000和JPEG-LS实现无失真即保真度高的压缩，压缩比通常为1.55～1.95［1-5］。然而，上述超光谱图像无损压缩算法复杂度较高，运算量大，应用硬件实现比较困难。

本文选取超光谱遥感图像作为本文的一类研究对象，研究压缩比不小于1.50的超光谱图像无损压缩算法，同时争取减小算法复杂度，以方便硬件的实现。

2 超光谱图像相关性分析及无损压缩方案

成像光谱仪有滤光片型、声光调制型、色散型等很多种类，由它们所成的图像即是光谱图像，超光谱图像即是光谱分辨率较高的光谱图像。本文研究通过推扫获得的“图谱合一”图像，它的超光谱图像信息需要从一组含有512帧的“图谱合一”的超光谱图像序列中进行无失真恢复［6］。本文所描述的超光谱图像指的是三维的“图谱合一”超光谱图像，它的相关性指空间相关性和谱间相关性。

在每一个谱段内某一点像素与其相邻点像素之间的相似性称为空间相关性。计算可知超光谱图像的行自相关系数最大为0.963 1、最小为0.962 7、平均为0.962 9，列自相关系数最大为0.961 4、最小为0.960 9、平均为0.961 1。由此分析，不管是行自相关系数还是列自相关系数均在0.96以上，行列之间的相关性大致相同，说明超光谱图像有较强的空间相关性。

在相同空间位置各波段光谱图像的像素相似性称为谱间相关性.这有以下两点原因：（1）相邻波段对空间地物的反射率是相近的，每一个波段图像的像素值是相同空间地物对各波段的反射强度值，由此具有很强的相关性；（2）不同的波段图像反映相似的地物目标，因此具备相近的空间上的拓扑结构［7］。经过分析可得，超光谱图像序列的谱段之间的相关系数最大为0.971 3、最小为0.955 7、平均为0.968 6，说明超光谱图像亦具有较强的谱间相关性。表1为对超光谱图像序列1001～1008进行相关性计算所得相关系数值。

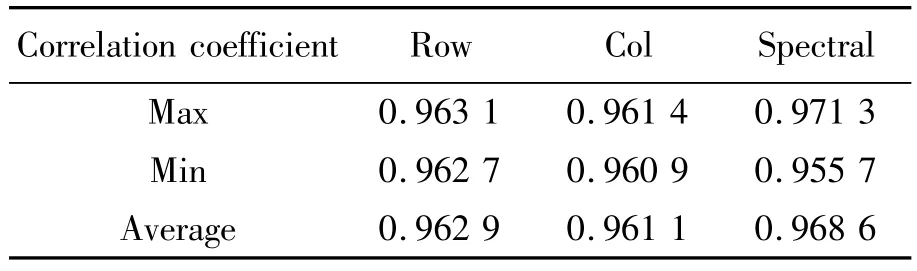
表1 8序列超光谱图像相关系数值Tab.1 Correlation coefficients of hyper-spectral image w ith eight sequences

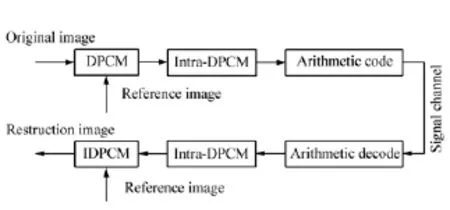
图1 超谱图像无损压缩原理示意图Fig.1 Lossless compression principle of hyper-spectral image

根据以上分析，以一组512帧的“图谱合一”序列图像作为对象展开研究，提出如下压缩算法：以超光谱图像序列前一帧作为后一帧的参考图像，第一步实施谱间预测，消除谱间存在的相关性；第二步对差分图像实施帧内预测，并对预测的差分码采用二值自适应算术编码，消除空间存在的相关性。图1是该方法的原理框图。

3 无损（无失真）压缩方案

3.1 谱间DPCM差分预测

相邻图像像素存在较强的相关性，当前像素值可通过之前的预测像素值预测，和实际值作差后得到预测误差。在相关性比较强的情况下，预测值和实际值最为接近，因此预测误差序列具备均值为零和方差最小的特性。若在整个压缩系统中不采用量化器，则可实现无损压缩。

应用谱间预测于超光谱图像序列（512帧）：第一，以序列1000作参考帧不进行压缩直接传输；第二，输入超谱图像序列1001，以序列1000作为参考帧然后应用谱间预测，得到谱间差分图像；第三，传输经后续处理的差分图像。在收报端，参考序列与接收的差分序列经逆预测得到恢复序列1001。同上，此后后一序列均以前一序列作为参考序列，按上述步骤完成512帧图像发送。因本文采用完全的无失真压缩，计算可知恢复序列和原始序列之间的均方误差为零，因此在收报端用恢复序列作为参考序列并未引入累积误差。

实际中，考虑有列的平移存在于试验用超光谱序列之间，而干涉条纹位置相对来说比较固定。对序列1001实施谱间预测，以序列1000作为参考帧，1001右移一列与1000作差得到差分图像，如此可得干涉条纹。而且，预测过程中仅实施移位和加、减法运算，硬件实现简便。

3.2 帧内预测

预测编码建立在图像中相邻像素间高度相关的事实上。其技术特点是像素值不直接传输，而是对实际像素值与它的预测值之间的差值进行编码和传输，此差值称作预测误差［8］。该方式削弱或消除了相邻像素间存在于时空上的冗余度，且在压缩系统中未使用量化器，则数据的无损压缩就成为可能。一般情况下预测误差的一阶熵远远小于原像素值的一阶熵，对预测误差首先进行量化再进行熵编码或对预测误差值直接进行单符号的熵编码，都要比直接对单像素值编码具备更高的效率。图2为本文算法预测器扫描像素示意图，预测器为X=A-（B+E）/2，X为待预测像素，A～E为已知像素。

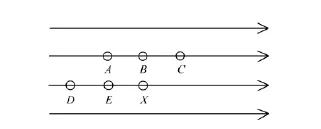
图2 预测器扫描像素示意图Fig.2 Schematic diagram of scan pixel by predictor

应用帧内预测于超光谱图像序列（512帧）：第一，不经压缩直接传输经谱间预测后的波段残差图像序列的第一行、第一列，作为序列的第一行、第一列；第二，对预测后序列（除第一行和第一列外）应用帧内预测，得到其差分码流；最后，传输经后续处理的差分码流。在接收端，收到的差分码流经逆预测得到恢复的波段残差图像序列。依此类推，按上述步骤完成512帧图像传输。

3.3 算术编码

通过对经帧内预测的差分码流应用二值自适应算术编码，该方法的基本原理和思想来自于自适应算术编码，同时应用整数加法和移位实现数据的压缩。和自适应算术编码相比，它可自动控制进位扩散并易于实现；和一般算术编码相比，具有更高的逼近准确度和极大的灵活性［9-12］。

4 实验分析

本文应用配置为Intel Core i5-3317u处理器、1.7 GHz CPU、4.00G内存的计算机进行算法仿真，以Matlab7.0作为仿真工具，以每帧8 bit的512帧“图谱合一”超光谱图像序列为对象，按上述方法依次压缩传输。

图3为以1000作为参考帧对1001进行压缩的图解，图3（a）和（b）分别为1001和1000原图，图3（c）为1001与1000谱间预测差分图像，图3（d）为图3（c）的帧内预测误差图像，图3（e）为1001恢复图像。图4为超光谱图像序列中的1001～1008帧图像的压缩比数据图。

表2为应用本文算法对超光谱图像1001～1008序列进行无损压缩得到的压缩比值，表3为应用不同算法对上述序列进行无损压缩得到的压缩比均值。本文算法压缩比平均达到1.662 0，经过计算验证，恢复帧和原始帧之间的均方误差为零，表明本文算法是完全无损的压缩。

图3 超光谱图像压缩仿真实验结果图Fig.3 Experimental results of hyper-spectral image compression

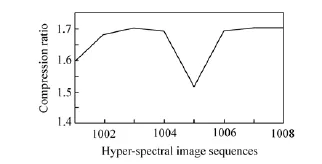
图4 超光谱图像序列压缩比数据图（1001～1008帧）Fig.4 Compression ratio of hyper-spectral images（frame1001-1008）

表2 8序列超谱图像压缩比值Tab.2 Compression data of hyper-spectral image w ith eight sequences

表3 8序列超光谱图像压缩比均值Tab.3 Compression ratio of hyper-spectral image w ith eight sequences

5 结论

本文算法采用帧内预测替代整数小波变换后，压缩比达1.662，表明通过谱间差分预测和帧内差分预测能够有效消除超光谱图像序列的谱间相关性和空间相关性，压缩比较二维整数小波变换算法提高了15.6%。

本文算法最大压缩比达1.704、平均压缩比达1.662，相比K-L变换算法有一定提高。本压缩算法中谱间预测仅需简单的加、减法和移位运算，帧内预测只有加、减法运算，算术编码也仅用移位和整数加法运算。因此，本文算法复杂度相对来说比较低，容易用硬件实现。

［1］张雷，黄廉卿.超光谱图像数据压缩方法综述［J］.光机电信息，2005，1（4）：30-33.ZHANG L，HUANG L Q.Summarization of hyper-spectral image data compression algorithms［J］.OME Information，2005，1（4）：30-33.（in Chinese）

［2］汤毅，辛勤，李纲，等.基于内容的高光谱图像无损压缩［J］.光学精密工程，2012，（3）：668-674. TANG Y，XIN Q，LIG，et al..Lossless compression of hyperspectral images based on contents［J］.Opt.Precision Eng.，2012，（3）：668-674.（in Chinese）

［3］张宁，吴银花，金龙旭，等.适于航天应用的高速SPIHT图像压缩算法［J］.液晶与显示，2011，26（6）：847-852. ZHANG N，WU Y H，JIN L X，et al..Image compression algorithm of high-speed SPIHT for aerial applications［J］.Chinese J.Liquid Crystals and Displays，2011，26（6）：847-852.（in Chinese）

［4］杨建强，侯建军，刘亮.基于K-means聚类和SPIHT编码的红外图像压缩算法研究［J］.光学与光电技术，2012，10（6）：94-97. YANG JQ，HOU J J，LIU L.Infrared image compression algorithm based on k-means clustering and SPIHT encoding［J］.Opt.Optoelectronic Technol.，2012，10（6）：94-97.（in Chinese）

［5］朱明，高文，郭立强.压缩感知理论在图像处理领域的应用［J］.中国光学，2011，4（5）：441-447. ZHU M，GAOW，GUO L Q.Application of compressed sensing theory in image processing［J］.Chinese Optics，2011，4（5）：441-447.（in Chinese）

［6］吴小华，李自田，张帆.干涉超光谱图像分析与近无损压缩CPLD实现［J］.光子学报，2005，34（9）：1346-1348. WU X H，LIZ T，ZHANG F.Analysis and near-lossless compression based on CPLD of interference hyper-spectral image［J］.Acta Photonica Sinica，2005，34（9）：1346-1348.（in Chinese）

［7］周有喜，肖江.遥感干涉超光谱图象压缩编码［J］.光子学报，2005，34（4）：594-597. ZHOU Y X，XIAO J.The image compression scheme for remote sense superspectral images［J］.Acta Photonica Sinica，2005，34（4）：594-597.（in Chinese）

［8］张春田，苏育挺，张静.数字图像压缩编码［M］.北京：清华大学出版社，2006. ZHANG CH T，SU Y T，ZHANG J.Digital Image Compression Coding［M］.Beijing：Tsinghua University Press，2006.（in Chinese）

［9］谢林，虞露，仇佩亮.基于上下文的自适应二进制算术编码研究［J］.浙江大学学报，2005，39（6）：910-915. XIE L，YU L，QIU P L.Resarch on context-based adaptive binary arithmetic coding［J］.J.Zhejiang Univ.，2005，39（6）：910-915.（in Chinese）

［10］严哲南，赵风光.一种适合硬件实现的高效算术编码［J］.通信学报，2000，21（2）：86-89. YAN ZH N，ZHAO F G.A efficient arithmetic codes suiting for hardware design［J］.J.China Institutes Communications，2000，21（2）：86-89.（in Chinese）

［11］尹传历，李嘉全.基于位平面的嵌入式超光谱图像压缩系统［J］.液晶与显示，2012（2）：245-249. YIN CH L，LIJQ.Embedded hyper-spectral image compression system based on bit-plane［J］.Chinese J.Liquid Crystals and Displays，2012（2）：245-249.（in Chinese）

［12］王建军，刘波.适于硬件实现的无损图像压缩［J］.光学精密工程，2011，19（4）：922-928. WANG JJ，LIU B.Hardware implementation of lossless image compression［J］.Opt.Precision Eng.，2011，19（4）：922-928.（in Chinese）

Hyper-spectral image lossless compressing based on spectral DPCM and intra-DPCM

WANG Jun
（The Ninth Institute，China Aero Space Science&Industry Corporation，Wuhan 430040，China）
*Corresponding author，E-mail：king090903@aliyun.com

By focusing on hyper-spectral remote sensing images，the spectral correlation and spatial correlation of images from an interferential imaging spectrometer was analyzed.A 3D Differential Pulse Code Modulation（DPCM）lossless compression schemewas submitted.This scheme includes three aspects：spectral DPCM，intra-DPCM to prediction error image and adaptive bit-level arithmetic coding to differential coefficients.The experimental data show that the algorithm has achieved lossless compression and the average of compression ratio is up to 1.662，15.6%increasement in comparison with that of the 2D integer wavelet transform.This algorithm uses addition-subtration and shifts to complete data compression，which is easier for hardware implementation.

hyper-spectral image；lossless-compressing；spectral Differential Pulse Code Modulation（DPCM）；intra-DPCM；adaptive bit-level arithmetic coding

TP751

10.3788/CO.20130606.0863