基于希尔伯特变化的微小振动激光多普勒信号处理

2013-04-27武颖丽吴振森

中国光学 2013年3期

关键词：希尔伯特振幅多普勒

武颖丽，吴振森

（西安电子科技大学理学院，陕西西安710071）

基于希尔伯特变化的微小振动激光多普勒信号处理

武颖丽*，吴振森

（西安电子科技大学理学院，陕西西安710071）

为了实现对固体目标微小振动参数的测量，建立了微小振动的激光多普勒信号模型。采用希尔伯特数字运算，将激光多普勒振动信号的即时信号采样转化为信号的谱采样。通过频谱计算得到每个振动周期中瞬时频率的平均数，应用差值采样序列积分计算得到振动频率，最后根据振动信号频率变化与振幅的关系得到振幅。采用希尔伯特方法对实验测试结果进行处理验证，并分析了误差来源。实验结果表明：实验测量目标的振动振幅约为1.85×10-4m，转动的圆频率约为170 Hz。因此，应用希尔伯特变换方法处理测量的目标微小振动信号，获取目标运动的参数是可行的。

希尔伯特变换；激光多普勒测振；微小振动；信号处理

1 引言

近些年，处理激光多普勒测振信号的数字方法已经有实际性的应用。李艳辉等人采用双光束干涉测量系统应用激光多普勒方法测量了微小阻尼振动［1］;周健等人针对减小载体振动对传统差动激光多普勒测速仪的测速精度，提出了Janus配置的差动激光多普勒速度计（LDV）［2］。在应用激光多普勒测速系统时，张建伟将Hilbert-Huang变换（HHT）应用于瞬时速度信号的分析中，提取了各阶内禀模态函数并通过经验模态分解（EMD）对速度信号进行了滤波降噪［3］。由于激光多普勒测量振动信号的振幅大小不同，因此相应的信号特征及处理方法也不同［4-6］，当振动振幅A大于条纹的间隔Λ时，常采用激光多普勒测振信号的振幅为零值的方法;如果振动的振幅A远小于Λ，常应用基波检测方法;如果振动的振幅A远大于Λ，则采用直接探测信号在每个振动周期输出零值数目的方法。然而这些方法主要应用电微型计算机处理光电探测器，通过高速逻辑数字转换来实现。信号处理常用的频率解调方法包括频率电压转换电路直接鉴频法、波形变化法、调频负反馈解调法和正交鉴频法等，不过微小振动的情况下，调频波的频移较小，采用这些方法进行解调的效果较差。

如果激光多普勒信号是窄带信号，数字希尔伯特变换技术就可以用于处理振动信号，并提取振动参数，这种变换在无线电工程合成信号处理领域有很广泛的应用。1998年，Grechikhin V首先应用数字希尔伯特变化处理激光多普勒振动信号，分析了振动信号特征［7］;2004年，谭善文等人应用希尔伯特-黄变换对采样的多普勒振动信号进行时间-空间滤波，并论证了其可行性［8］;2011年，何俊峰等人基于希尔伯特-黄变化和Savitzky-Golay滤波，给出了应用希尔伯特-黄变化对半导体激光云高仪后向散射信号去噪的方法［9］。本文在此基础上讨论了应用希尔伯特变换对微小正弦振动情况下的多普勒信号进行解调，给出了振动幅度是条纹间隔的0.1～10倍情况下的数字处理方法，并最终获取了振动参数。

2 激光多普勒测振信号模型

激光多普勒测振实验信号形式如下：

式中：U0为常数，ωs为未知频率，Λ为条纹间隔，A为振动振幅，ωv为振动频率，φ，β为初始相位。

设参数U0=1，A/Λ=1，ωs/ωv=20，则振动信号曲线如图1。

图1 振动多普勒信号Fig.1 Time dependence curves of LDV signal

根据式（1），信号的相位为：

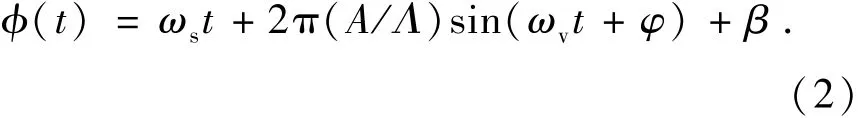
信号的瞬时频率ω（t）与相位的关系为：

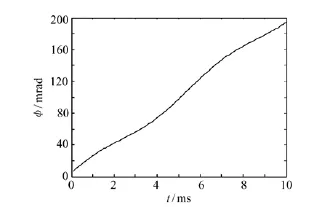
图2 瞬时相位曲线Fig.2 Time dependence curve of LDV signal instantaneous phase

瞬时频率和相位波形如图2和图3所示。当式（3）取最大值时，设信号的频率变化为Δω= ω（t）-ωs，则可以得到振动振幅：

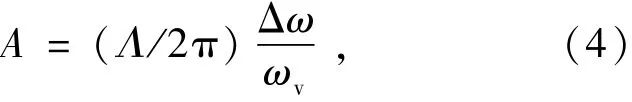
式中，Δω为式（1）中信号频率的变化量。

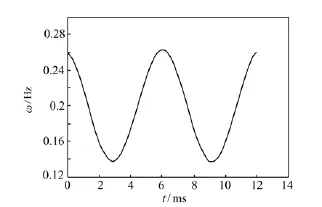
图3 瞬时频率曲线Fig.3 Time dependence curve of LDV signal instantaneous frequency

3 测量方法

根据前述理论，当信号的瞬时值为U（t）= U0cosφ（t）时，通过瞬时信号值U（t）不能直接得到U0，φ（t），因此利用窄带信号矢量模型，采用希尔伯特解调原理处理信号。

3.1 希尔伯特变换解调原理

用希尔伯特变换把一个实信号表示为复信号（即解析信号），不仅使理论讨论更加方便，更重要的是可以由此研究实信号的包络、瞬时相位和瞬时频率。

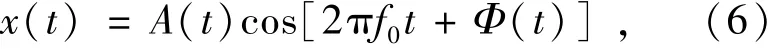
式中：A（t）描述振荡幅度变化，当A（t）变化缓慢时，A（t）起到振动函数cos［2πf0t+Φ（t）］的包络作用，因此A（t）称为窄带信号的包络。由希尔伯特变换原理，x（t）的希尔伯特变换为：

因此，构成解析信号：

式中：f0为频率，给出了调幅信号的包络—调制信号的信息。在这种情况下，希尔伯特变换可用于幅值解调。

式中，f0为频率，Φ（t）为相位相调制量。

x（t）的瞬时相位为：

相位调制信号：

根据相位调制与频率调制的关系得，实信号x（t）的频率调制信号：

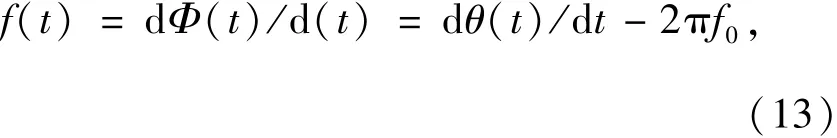
由此可以得到调相信号x（t）的相位和频率调制信息，在这种情况下希尔伯特适用于相位解调和频率解调。

将以上希尔伯特变换原理用于处理微小振动的多普勒信号。设微小振动窄带信号为：

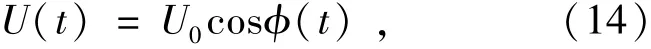
式中：U0为窄带信号幅值，φ（t）信号相位。对U（t）进行希尔伯特变换为：

通过这个变化，U（t）和U′（t）构成一个复数信号U（t）：

式中，U（t）=［U2（t）+U′2（t）］1/2，瞬时相位为：

又由式（2）得到相位调制信号：

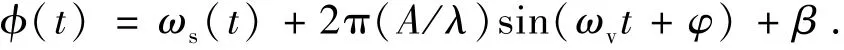
根据相位调制与频率调制的关系，得到实信号U（t）的频率调制信号：

由此可得到调频信号U（t）的相位和频率调制信息。

3.2 希尔伯特变换解调过程

假设频率变化信号Δω=2π（A/Λ）ωv是一个小量，这样在希尔伯特的数字运算中，信号U（t）可以用N维瞬时取样信号值的矩阵哉（kT0），k=1，…，N代替，其中T0为取样间隔。为了确定取样信号，应用希尔伯特共轭信号谱线估计，根据共轭信号的谱线密度定义：

式中：SU（ω）为信号U（t）的谱密度。激光多普勒振动的即时采样信号可转化为信号的谱采样，而共轭信号可以通过数字傅里叶逆变化得到。假设已知振动频率ωv，采样间隔T0固定，观测间隔NT0的时间即等于整数个振动周期。每个振动周期的采样数n=2π/（ωvT0），每个振动周期中心信号频率ωs的采样数m=2π/（ωsT0），则每个振动周期中瞬时频率的平均数ω（t）可以通过频谱计算来确定，而频率的平均值可以得到频率变换ωs，又根据式（16）可以确定ω（t）与ωs的差值，并进一步应用差值采样序列积分计算得到频率变化Δω=2π（A/Λ）ωv，最后根据式（4）定义得到振动振幅A。

4 测量实验与结果

4.1 实验测试及信号处理

实验系统由步进电机控制，通过软件编程使得目标进行简谐振动，激光多普勒振动测量实验系统如图4，实验装置如图5所示。入射光源激光波长为632.8 nm，光电探测器选用响应时间为ns量级的PIN，采样数字示波器的分辨率为500 MHz。图6为实际测量得到的差拍信号，图7为希尔伯特滤波后的信号;应用希尔伯特变换进行信号处理得到幅度信号（如图8）和瞬时相位信号（如图9）。从图中可以得到振动振幅约为1.85×10-4m，进一步应用前面理论计算的圆频率约为170 Hz。

图4 激光多普勒振动测量实验系统图Fig.4 Schematic diagram of laser Doppler vibration measurement system

图5 激光多普勒振动测量实验装置图Fig.5 Experimental apparatus for laser Doppler vibration measurement

图6 测量的电压（强度）信号Fig.6 Curves ofmeasured voltage signal

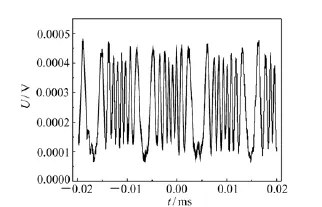
图7 滤波后的电压（强度）信号Fig.7 Curves of voltage signal after digital filtering

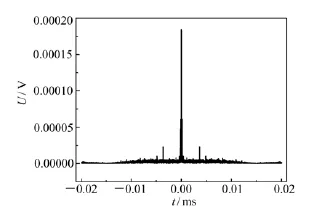
图8 振幅信号Fig.8 Curve of amplitude signal

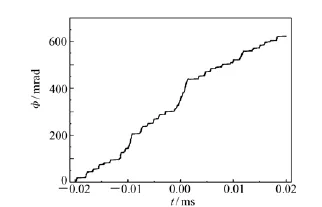
图9 瞬时相位信号Fig.9 Curve of instantaneous phase signal

4.2 误差分析

振幅的相对误差主要来源于条纹间隔校准误差和变化频率的估计误差，即：

式中，δA为振幅相对误差，δΛ为条纹间隔标准误差，δΔω为变化频率估计误差。

频率的平均值ωs和变化频率Δω包含在采样信号U（KT0）的N序列中，因此，参数ωs，Δω的估计误差由信号采样误差决定，而采样信号的误差与信噪比、信号的量化电平、信号U（t）的带宽限制、时间间隔的观测、取样序列的大小N等因素有关。频率平均值的计算和变化是通过瞬时频率采样ω（KT0）运算处理得到的，因此这个参数误差的估计取决于瞬时频率估计的误差。

图10给出了幅度的相对误差依赖信号谱带宽的关系曲线，可以看出振动相对幅度参数的相对误差依赖于参数2ΔΩ/Ωs的值。当振动振幅与条纹间隔比值为0.1时，每个振动周期中心信号频率的采样数m≤2，此时，抽样定理不满足数字信号处理过程，这种情况下会引起时间间隔变宽，中心信号频率的振动周期采样数值减小，振动振幅的相对误差变大。如果对于时间间隔进行窄带监测，则幅度的相对误差会因为数字信号谱带宽的增加而增加，这种情况下则需要考虑用快速傅里叶变化的算法来处理。

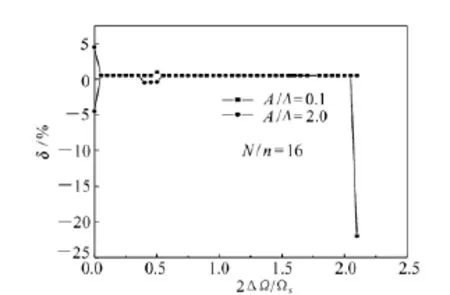
图10 幅度相对误差Fig.10 Relative error curve of vibration amplitude

5 结论

应用数字希尔伯特变换处理振动的激光多普勒信号，给出了具体解调原理和解调过程。进一步应用该方法对目标微小振动的激光多普勒信号进行解调，获得了微小振动的振幅和相位的变化，并分析了测量获得的振动信号的相位和幅度的误差来源。与传统的外差多普勒信号的求积过程算法相比，应用数字希尔伯特变化的方法可以直接给出未知振幅和相位变化。

参考文献：

［1］李艳辉，吴振森，武颖丽.基于激光多普勒法测量微小阻尼振动［J］.中国激光，2010，37（1）：231-235 LIY H，WU ZH S，WU Y L.Small damping vibration measurement using laser Doppler effect［J］.Chinese J.Lasers，2010，37（1）：231-235.（in Chinese）

［2］周健，龙兴武.载体振动对差动激光多普勒测速仪的影响［J］.强激光与粒子束，2011，23（2）：157-160. ZHOU J，LONG XW.Influence of vehicle′s vibration on dual-beam laser Doppler velocimeter［J］.High Power Laser and Particle Beams，2011，23（2）：157-160.（in Chinese）

［3］张建伟，苗超.撞击流混合器速度信号的Hilbert-Huang变换分析［J］.实验流体力学，2010，4：66-70. ZHANG JW，MAO CH.Hilbert-Huang transform of velocity signal in impinging stream mixer［J］.J.Experiments in Fluid Mechanics，2010，4：66-70.（in Chinese）

［4］KARASIK A Y，RINKEVICHIUS B S，ZUBOV V A.Laser Interferometry Priniciples［M］.Moscow：Mir Publishers and CRC Press，1995.

［5］GRECHIKHIN V A.The analysis of the computer techniques for LDA signal processing［J］.OpticalMethods for Flows Investigation，1995：23-25.

［6］武颖丽，吴振森.旋转粗糙圆柱的激光散射功率谱分析［J］.光学精密工程，2012，20（12）：2654-2660. WU Y L，WU ZH S.Analysis of power spectra for laser scattering intensity on rotating cylinder targets［J］.Opt.Precision Eng.，2012，20（12）：2654-2660.

［7］GRECHIKHIN V，RINKEVICHIUSB.Hilbert transform for processing of laser Doppler vibrometer signals［J］.Opt.Lasers Eng.，1998，30（2）：151-161.

［8］谭善文，秦数人，汤宝平.Hilbert-Huang变换的滤波特性及其应用［J］.重庆大学学报，2004，27（2）：9-12. TAN SH W，QIN SH R，TANG B P.The filtering character of hilbert-huang transform and its application［J］.J. Chongqing University，2004，27（2）：9-12.（in Chinese）

［9］何俊峰，张玉钧.基于希尔伯特-黄变换的激光云高仪后向散射信号去噪方法［J］.光学学报，2011，31（2）：1-10. HE JF，LIUW Q，ZHANG Y J.A denoisingmethod for backscatter signal of laser ceilometer based on Hilbert-Huang transform［J］.Acta Optica Sinica，2011，31（2）：1-10.（in Chinese）

M icro-vibration laser Doppler signal processing based on Hilbert transform

WU Ying-li*，WU Zhen-sen
（School of Science，Xidian University，Xi′an 710071，China）
*Corresponding author，E-mail：ylwu@xidian.edu.cn

Tomeasure themicro-vibration parameters of a solid target，the laser Doppler signalmodel ofmicrovibration for the solid targetwas established.First，the laser Doppler vibration instantaneous sampleswere converted into signal spectral samples based on Hilbert transform.Then，themean value of the instantaneous frequency per vibration period was determined by spectralmethod，the value of vibration frequency was obtained by the quadrature procession of the difference sample sequences，and the amplitude was estimated according to the relation between frequency deviation and amplitude of vibration signal.Finally，experimental resultswere verified according to the Hilbertmeasuringmethod and the error sourcewas analyzed.Experimental results indicate that the vibration amplitude of the target is about1.85×10-4m，and the rotation frequency is about 170 Hz.It is feasible to obtain themotion parameters by using Hilbert transform tomeasure targetmicrovibration.

Hilbert transform;laser Doppler vibration measurement;micro-vibration;signal processing

TN247；TB936

10.3788/CO.20130603.0415