基于统计分析的葡萄酒的评价
2013-04-25史少云吕光阁
陈 然, 史少云, 张 悦, 吕光阁
葡萄酒是一种成分复杂的酒精饮料,不同产地、年份和品种的葡萄酒成分不同。葡萄酒的质量与其成分关系密切,是其外观、香气、口味、典型性的综合表现,主要依靠专家的感官进行评价。参考国内的相关研究文献,对葡萄酒分级分类的相关文献颇多。例如王金甲[1]根据葡萄酒物理化学性质,提出了一种葡萄酒质量评价新方法,且具有可视化的优点;李运[2]等将统计学方法应用于葡萄酒质量分析与评价中,为葡萄酒的质量控制、预测、预报、区分提供一种有效的途径;刘延玲[3]建立一种新的 Hopfield 神经网络分类器模型,通过训练单层前向神经网络来设计,可以直接处理葡萄酒的理化性质测试指标数据和专家的感官评价等级数据,实现葡萄酒质量分类。然而,提供葡萄品种的理化指标数据和对应葡萄酒的质量评分来确定葡萄等级的研究,国内外不多见。基于上述研究,本文采用相应的统计数据处理方法[4],根据评酒员的评价结果,确定两组红葡萄酒、白葡萄酒之间是否有显著性差异,并判断哪组可信;通过酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级。
1 F检验判断显著性差异
计算F统计量
(1)
其中,σ1,σ2是第一、二组方差m1,m2是第一、二组自由度
取一个显著性水平owuwx或0.05),可查表得到Fα(m1,m2),判断若F>Fα,则认为模型是显著的。
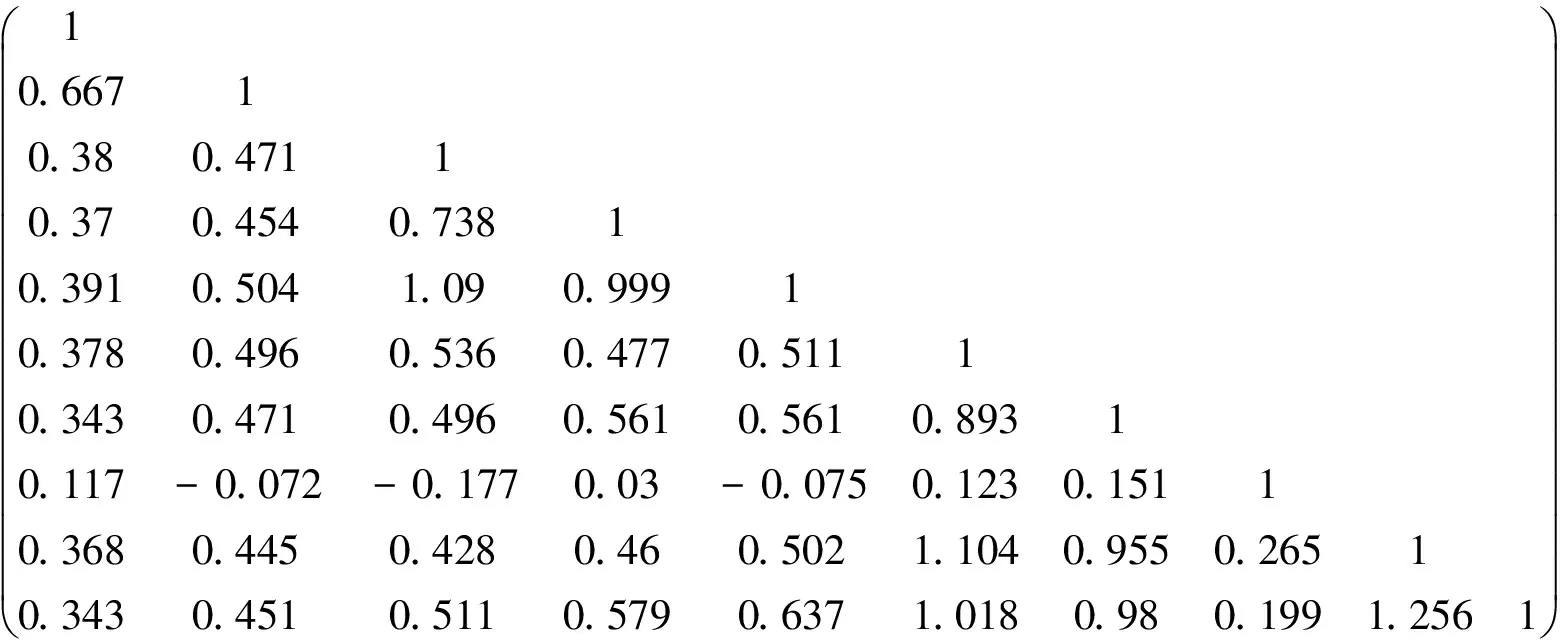
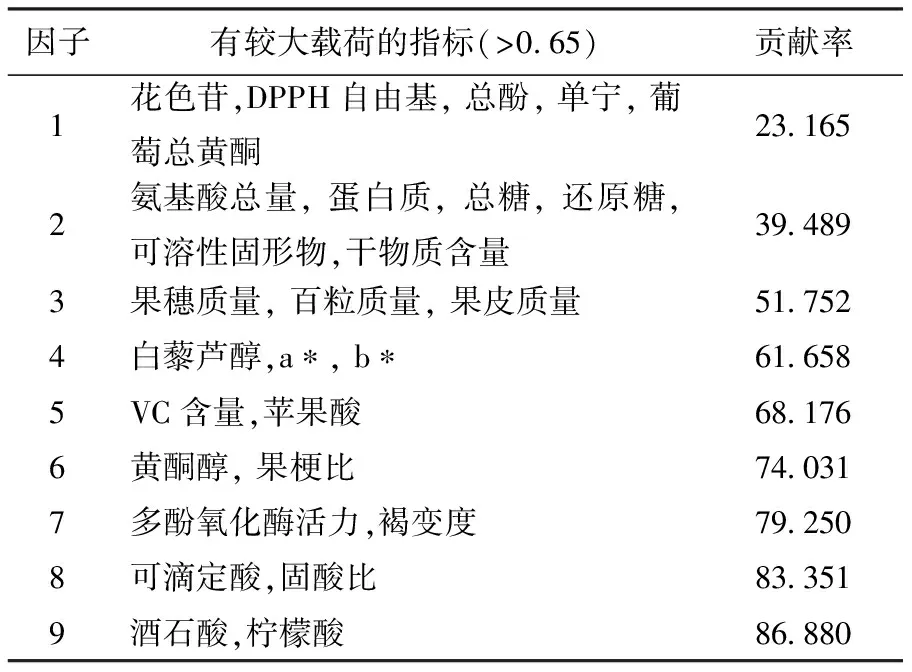
若F 利用Matlab7.6.0的anova21函数进行双因子可重复方差分析,可得到每种样品酒的检验结果如表1。 表1 样品酒的检验结果 其中SS-误差平方和;df-自由度;MS-均方差;F-显著性统计量;Fα-基于显著性水平为0.01的F值。 分析表1的四组显著性检验数据,基于“行”与“列”的双向显著性差异检验中,八组数据序列的F 统计量均大于基于显著性水平为 0.01 的F值,表示其差异性极显著。因此,两组评酒员对红葡萄酒,白葡萄酒的评分结果都具有显著性差异。 在评判过程中,如果评分者严格依据一套评分标准,并且在整个评分过程中保持一致,这样的评分结果是可信的[5]。但事实是任何评分情况下,评判、评分的顺序都会影响评分者,应用评分标准不一致,从而导致测量的误差,影响测量的精确性。 采用多系列相关分析,以第一组白葡萄酒为例,我们利用SPSS中“分析”→“相关”→“两因素”得到评酒员评分的相关矩阵,由公式Zr=atanh(r)得到Z矩阵 先求出Z值的平均值22387/45=0.497,再将此值代入下列Spearman-Brown校正公式[6]: 其中,n为品酒员人数;rAB为Z值平均值;Rtt为从Z 转回Spearman相关系数代表品酒员之间的信度。 计算得到Rtt=0.906。带入r=tanh(z)得到r=0.7192。因此对于第一组白葡萄酒10名品酒员的信度是0.72.同理,可得第二组品酒师的信度是0.70。 同样运用上述方法来求对红葡萄酒的评价,得到结果为第一组评论员的信度为0.72,第二组评酒员的信度是0.66。 综合两组对白、红葡萄酒的评价信度,可以得出结论:第一组评酒师更可信。 层次分析法,简称 AHP,是由美国运筹学家T.L.Saaty教授提出的一种定量和定性相结合的多目标层次分析方法[7]。该方法的原理是将决策者的经验判断加以量化,从而为决策者提供定量形式的决策依据。应用 AHP 方法计算指标权重系数,在层次阶递的指标系统的基础上,运用先分解后综合系统思想通过指标间的两两对比,并利用对比优劣的结果来综合计算出各指标的权重系数并作出排序[8]。 3.1.1 数据标准化处理 由于不同理化指标数值大小不同,数据波动范围不同,为了消除这些因素的影响,我们先对理化指标进行标准化处理。公式如下: 3.1.2 葡萄的理化指标数据的相关性分析 为了确定是否有必要使用主成分分析法,我们首先进行了变量相关性分析。以红葡萄为例,利用SPSS统计软件对这55个自变量和因变量做相关性分析,得到各个变量之间的相关性系数。从结果中可以看出:氨基酸总量和蛋白质均呈显著相关性,VC含量和氨基酸总量,蛋白质,花色苷,酒石酸,苹果酸均有相关性。由此我们认为,有必要使用主成分分析来降维、简化数据,并研究变量之间的关系。 3.1.3 主成分分析降维处理 利用SPSS中“分析”→“降维”→“因子分析”得到降维处理的数据如表2。 表2 SPSS中因子分析 关于酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄的影响,我们用层次分析法来分析。 3.2.1 递阶层次结构的建立 根据所确定的主因子,构造层次结构模型,本题中最高层是酿酒葡萄的分级,中间层是葡萄的9个理化主指标和葡萄酒的质量指标。 3.2.2 构造判断矩阵 记aij为第i和第j因素的重要性之比,表3列出Saaty给出的9个重要性尺度及其赋值。 表3 1-9尺度 由主成分分析法将9个理化指标的权重根据它们的方差贡献率来确定,因为方差贡献率反映了各个主成分的信息含量多少。因此我们只需确定理化指标和酒的质量指标的权重,得到判断矩阵A 求出其最大特征值为λ=10.369。 计算矩阵A的关于λ的特征向量,得到各指标对葡萄分级的权重如表4。 表4 指标对葡萄分级的权重 3.2.3 权值合理性检验 下面进行对判断矩阵C的一致性检验: (i) 计算一致性指标CI (ii) 查找相应的平均随机一致性指标RI 经查表知n=10 时,RI=1.490 (iii) 计算一致性比例CR 因此,我们认为判断矩阵具有满意的一致性。 为了统一单位,将指标进行归一化处理, 其中,rmax,rmin分别为同一评价指标下指标的最大值和最小值。 那么最终评分公式是: 根据得分,分级如表5: 表5 红葡萄级数和白葡萄级数 由表5数据可知,红葡萄跟白葡萄的等级划分情况均呈现极大部分样本隶属于C和D两个等级,整体趋势大致表现为“中间高,两边低”的分布。结合实际情况考虑,由于酿酒工业水平,环境等拮抗因素葡萄一般处于中等水平,因此,上表的数据整体分级情况较为理想。 本文所建立的模型展现出酿酒葡萄的各项理化指标和葡萄酒的理化指标的相关关系,可以较客观的对葡萄酒进行等级划分。利用主成分分析出的理化指标,可以针对性的优化酿酒葡萄的种植,从而高效的产出用于酿造高质量葡萄酒的酿酒葡萄,达到高效益的葡萄种植与生产。此模型也可推广用于各类多指标的物品中,提炼主要指标,简化数据,在社会生活中有很广泛的作用。 [参 考 文 献] [1] 王金甲,尹 涛,李 静,等.基于物理化学性质的葡萄酒质量的可视化评价研究[J].燕山大学学报,2010, 34(2):133-137. [2] 李 运,李记明,姜忠军.统计分析在葡萄酒质量评价中的应用[J].酿酒科技,2009 (4):79-82. [3] 刘延玲.新的Hopfield神经网络分类器在葡萄酒质量评价中的应用[J].价值工程,2012(2): 181-182. [4] 2012年全国大学生数学建模竞赛A题数据[EB/OL].(2012-9-7) http://www.mcm.edu.cn/html-cn/block/c61dfec317d7a5bd9b2b8efed81c8af3.html. [5] 徐林生,王执铨,戴跃伟.评审专家可信度评价模型及应用[J].南京理工大学学报(自然科学版),2010,34,2-46. [6] 汪顺玉,吴世银.评分员信度的多系列相关分析方法原理及运用[J].重庆邮电学院学报,2006(6):20-76. [7] Saaty, T.L. The Analytical Hierarchy Process, McGraw-Hill, 1980. [8] 戚黎蔚.AHP层次分析法在ITAT创业投资项目风险评估中的应用研究[D].上海交通大学,2008:30.
2 多系列相关分析方法分析可信度
3 基于主成分分析的AHP评价模型
3.1 葡萄的理化指标的确定

3.2 层次分析法的建立



3.3 评分公式的确立

4 结束语
