基于复数陷波器的窄带干扰抑制研究

解朦朦，王勇超

(西安电子科技大学 综合业务网国家重点实验室，陕西 西安710071)

扩展频谱通信技术是常用的通信抗干扰技术。从原理上讲它能有效地对抗窄带干扰、多频干扰，而且扩频增益越高，其干扰容限也越大。其较强的抗干扰、抗衰落和抗多径性能以及频谱利用率高、多址通信等诸多优点越来越为人们所认识，并被广泛应用于军事通信和民用通信的各个领域。但当干扰幅度较大时，单纯的扩频通信体制对干扰的抑制不够，就会造成大量误码，使通信系统的性能降低。因此，有必要考虑在解扩前加预处理模块，进行抗干扰处理。由于扩频信号的频谱类似于白噪声频谱，采用自适应滤波进行谱白化可以有效削弱这样的强干扰以获得更高的干扰容限。在雷达、通信等系统中，实际信号可能包含同相和正交分量，其样本为复数，因此复数自适应陷波器也逐渐被应用到各个领域［1－2］，针对信号中含有的多个单/多频信号，本文给出了一种基于LMS算法以及LBFGS算法的二阶复数自适应陷波器的实现方案。仿真结果表明，这种级联结构的复数自适应陷波器能快速跟踪并有效抑制强单/多频信号，对输入的宽带信号损伤小。

1 一阶限制零极点自适应复数陷波器分析

一阶限制零极点位置的自适应复数陷波器的结构［3］如图1所示。通过自适应迭代算法，前级A(Z)中的复系数h在不断修改，后级B(z)的复系数h'=rh随之相应改变。若迭代算法的修改对象为h=ejω中的ω，且0＜r＜1，则如图2所示陷波器的零点位于单位圆上，极点在零点和圆心的连线上且在单位圆内，陷波器始终能工作在稳定状态。由于后级B(z)对前级A(z)的幅频特性和相频特性的补偿，使得整个陷波器只在陷波频率处陷波，对其它频率上的信号放大量基本为1，相移近似为0。因此它可大幅度削弱强干扰，而引入的信号失真很小，使系统的干扰容限显著提高。

图1 一阶陷波器结构

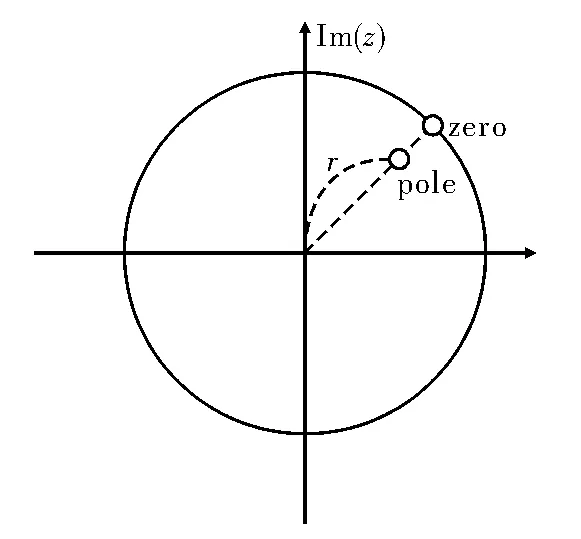
图2 一阶陷波器零极点分布图

陷波器传输函数为

陷波器3 dB带宽为［4，8］

设陷波器的输入和输出信号序列分别为{x(k)}和{e(k)}，由式(1)可写出一阶陷波器的差分方程

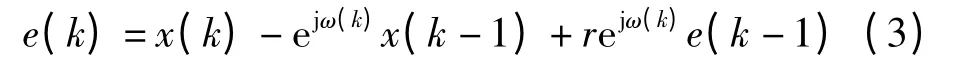
2 二阶复数陷波器及所用迭代算法分析

以一阶复数自适应陷波器为陷波单元，级联构成二阶复数自适应陷波器，其结构框图如图3所示。

图3 二阶复数陷波器结构

二阶陷波器由两个一阶陷波器级联构成，两个陷波器同时工作，接收信号x(k)先通过第一个陷波器，得到输出e(k)，e(k)通过自适应迭代算法控制第一个陷波器参数ω1(k)的迭代更新，同时其输出作为第二个陷波器的输入，得到最终的输出信号y(k)，y(k)通过自适应迭代算法控制第二个陷波器参数ω2(k)的迭代更新，自适应算法采用LMS算法或LBFGS算法。ω1(k)、ω2(k)的迭代更新步骤与一阶陷波器ω(k)的迭代更新步骤相同。

2.1 LMS算法分析

将陷波器的输出e(k)作为误差信号，其均方误差为J(ω)

其中，Im(·)表示取虚部;E(·)表示数学期望。

ω(k)的更新算法可描述为

LMS迭代算法［9］的实现步骤如下，对于每一个输入的样值x(k):第1步初始化，令e(0)=x(0)=0，ω(1)=0;第2步由式(3)，式(6)计算e(k)和L(k);第3步由式(9)更新得到ω(k+1)，k=k+1，返回第2步。

2.2 LBFGS算法分析

L－BFGS(Limit－Memory BFGS)算法［10］是限制存储量拟牛顿算法的一种，是BFGS算法的改进形式。其基本思想是:定义存储量m，只存储最新迭代的m个斜率信息，并用这些信息校正近似Hessian矩阵;抛弃早期迭代的斜率信息，因为它们对于当前的Hessian矩阵没有太大影响。换而言之，L－BFGS并不直接产生和存储每次迭代需要的Hessian矩阵，而是维护一个列表，该列表存储了最近m次迭代的变量ω和梯度g的信息，这些信息可以用来近似需要的Hessian矩阵。

假设sk=ωk+1－ωk，yk=gk+1－gk搜索方向由如下方式得到

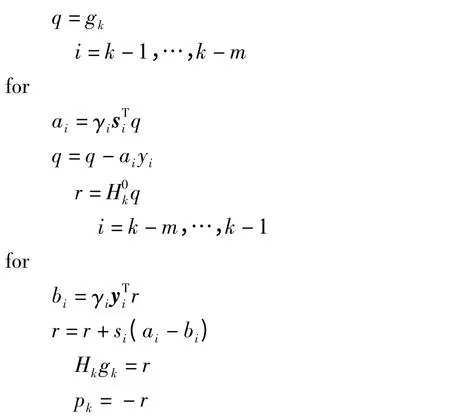
其中，gk为目标函数的梯度;在本文中目标函数为;ωk为所求的变量;m用来控制所需的存储量;为初始对称正定矩阵(常取为单位矩阵I);pk就是所求的搜索方向。

LBFGS迭代算法的实现步骤如下:

第1步初始化ω0，m＞0，k:=1;

第3步更新变量ωk+1=ωk+pk×αk，计算gk+1;

第4步如果k＞m，从存储中抛弃{sk－m，yk－m}，转到第5步，否则，直接跳到第5步;

第5步计算并存储sk=ωk+1－ωk，yk=gk+1－gk，k:=k+1，返回第2步。

3 实验结果与讨论

为验证本文所采用滤波器的性能，设计以下实验来考察不同算法的收敛特性和陷波器的陷波效果，并假设陷波器的输入x(k)是在扩频信号中叠加了幅值不同的两个单频干扰。

实验1 设x(k)包含两个单频干扰n1=A1ej2π·0.1k，n2=A2ej2π·0.95k(k=1，2，3，…)，单频干扰强度A1=70，A2=7，ω1(0)=0，ω2(0)=0，极点半径r(0)=0.85，r(∞)=0.98，采用Armijo准则计算搜索步长。在此条件下分别采用LMS算和LBFGS算法得到的仿真结果如图所示。

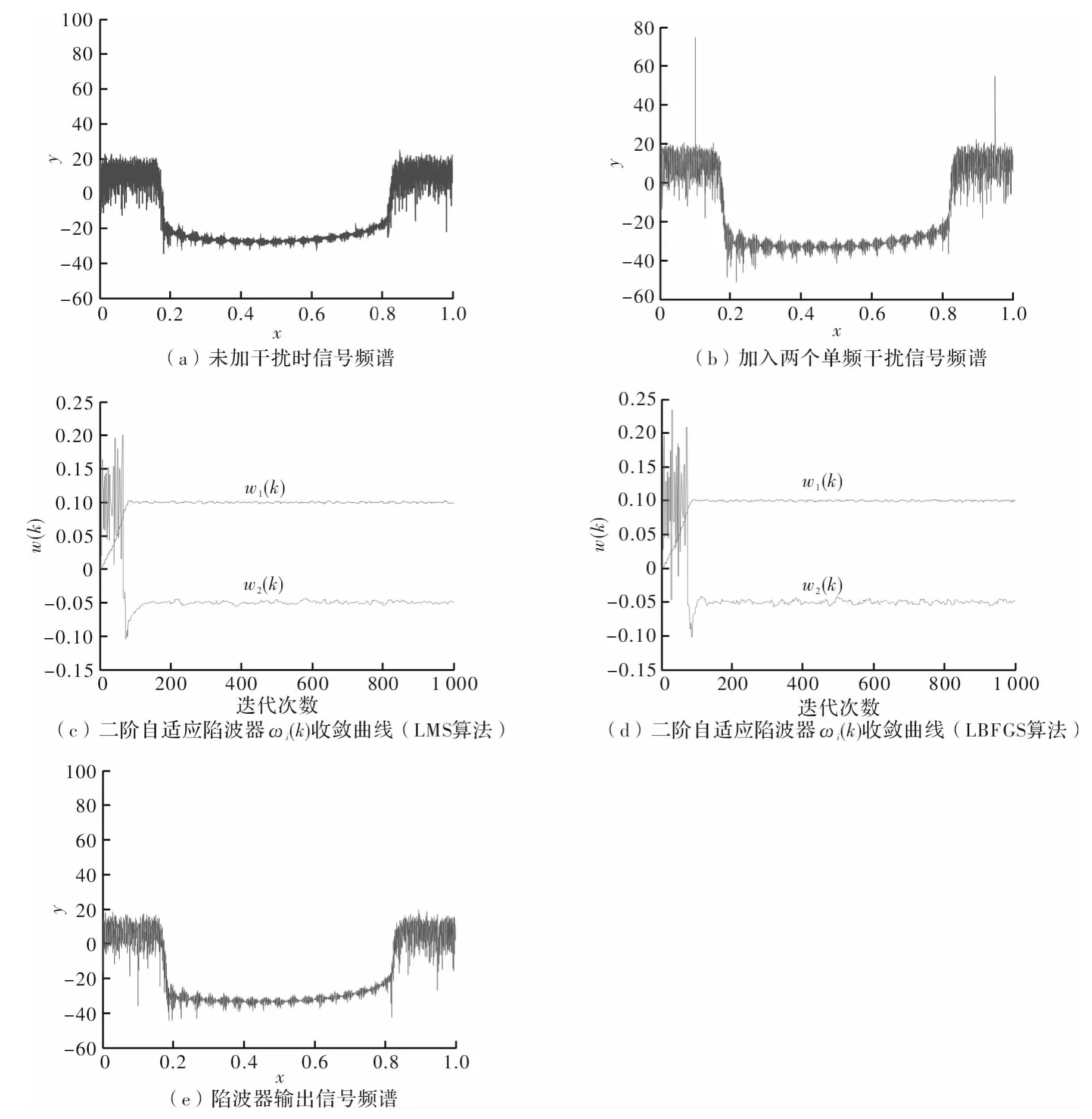
图4 实验1仿真结果

实验2把实验1中ω1(k)、ω2(k)的初始值改为ω1(0)=0，ω2(0)=π其他条件不变，仿真结果如图5所示。

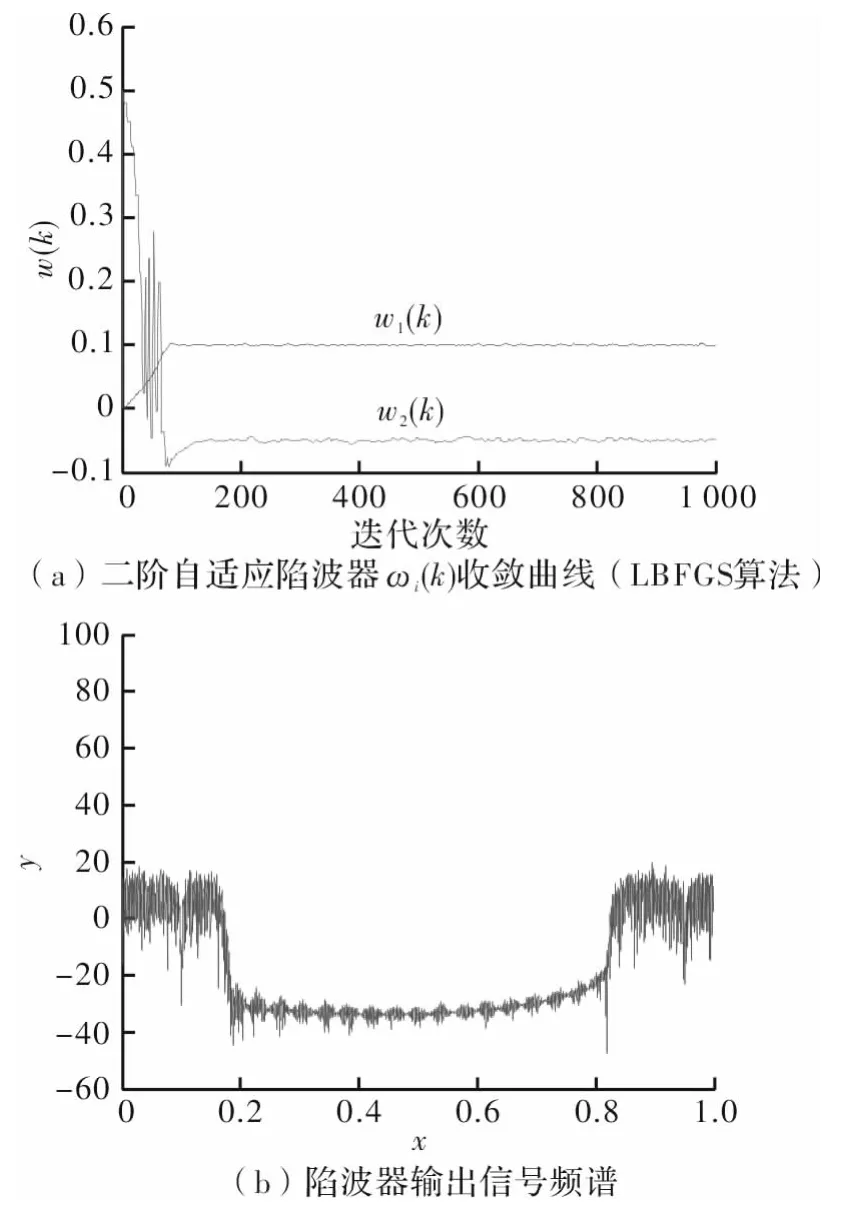
图5 实验2仿真结果

实验3 设x(k)包含两个单频干扰n1=A1ej2π·0.02k，n2=A2ej2π·0.05k(k=1，2，3，…)单频干扰强度A1=70，A2=7，ω1(0)=0，ω2(0)=0，极点半径r(0)=0.85，r(∞)=0.98，采用Armijo准则计算搜索步长，在此条件下分别采用LMS算法和LBFGS算法得到的仿真结果如图6所示。

实验4把实验1中ω1(k)、ω2(k)的初始值改为:ω1(0)=0，ω2(0)=2，其他条件不变，仿真结果如图7所示。

仿真结果表明，对于幅值不同的干扰，采用本文所用结构的陷波器，可以把干扰陷掉，而且只在单频点处陷波，在有效抑制单频干扰的同时，对宽带信号的损伤较小。对于本文所采用的两种迭代算法，ω1(k)和ω2(k)具有良好的收敛性，并且其初始点可以随意选取。文献［5～7］中的Gradient－based算法在针对两个单频干扰时却需要近400次的迭代才能收敛，而且陷波单元频点的初始值要选的与最优值接近。可见本文的算法具有更快的收敛速度。

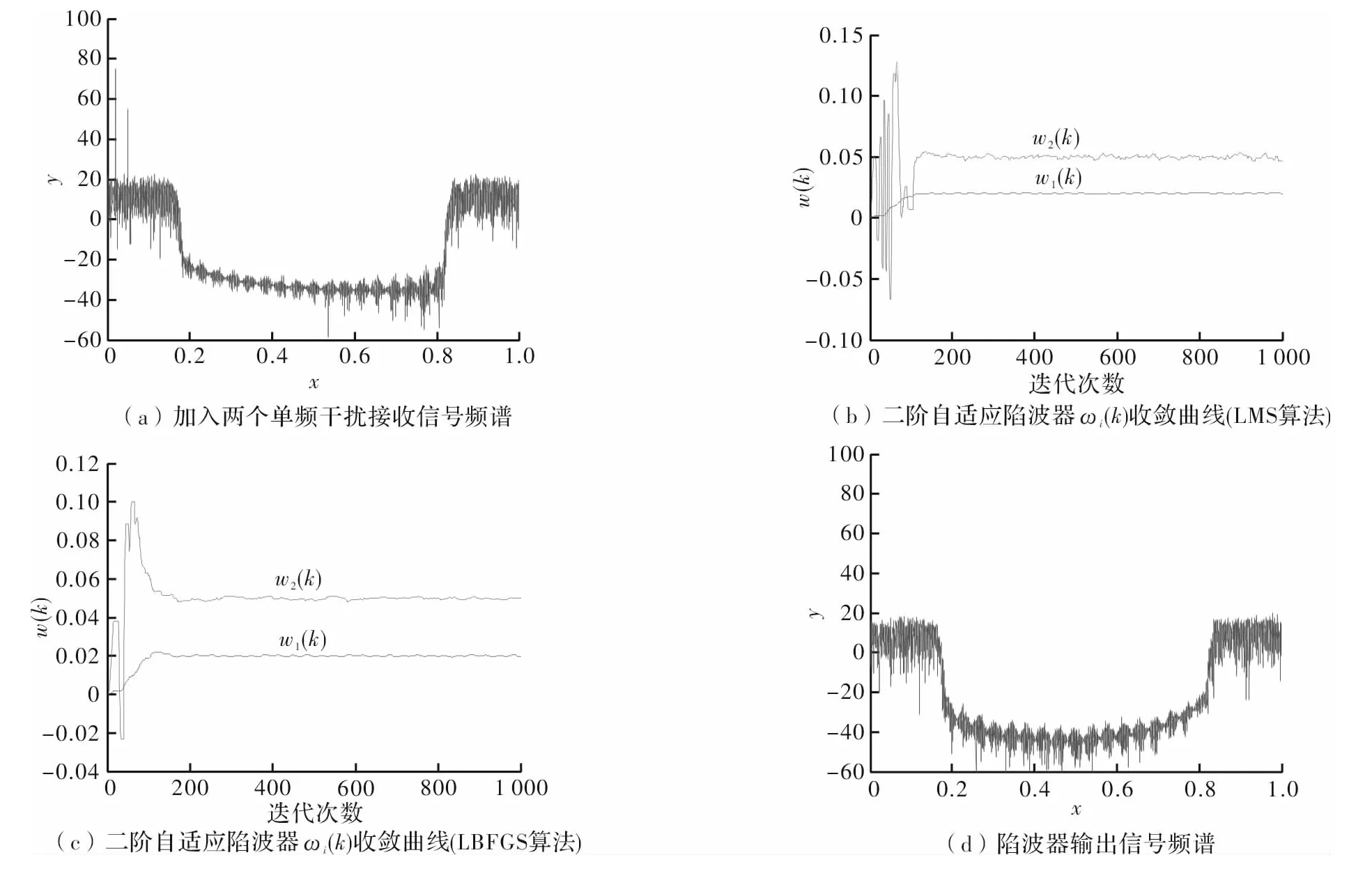
图6 实验3仿真结果

若采用文献［3］所提出的矩阵型高阶陷波器，要陷掉两个干扰则需要4个一阶陷波器，陷波单元的频点初始值不能设为相同值，否则算法不收敛。当加入本文所加干扰的时，在相同的条件下，仿真结果如图8所示。

仿真结果表明，当加入的干扰幅值不同，特别是当干扰幅值较小时，文献［3］所提出的矩阵型高阶陷波器不能够陷掉干扰，算法不能收敛。

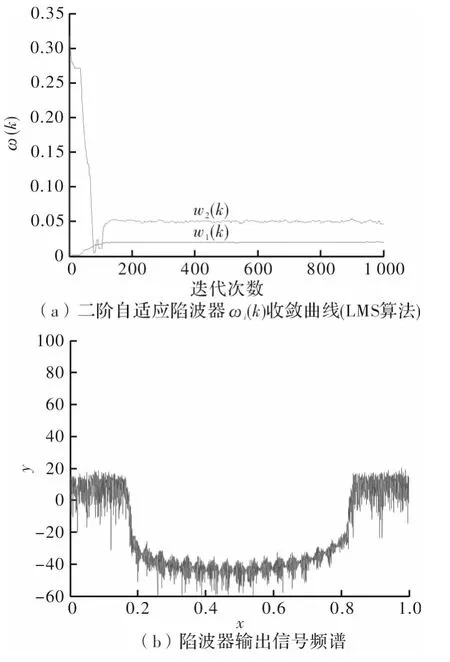
图7 实验4仿真结果

图8 采用文献［1］所用结构陷波器仿真结果

4 结束语

针对幅值相差较大的干扰，本文提出了一种将一阶陷波器作为陷波单元级联构成二阶陷波器的方案，讨论了两种迭代算法LMS算法和LBFGS算法以及把这两种迭代算法用于该陷波器的收敛性。仿真结果表明，采用本文所提结构的陷波器可以有效地抑制幅值不同的两个干扰，对输入陷波器的宽带信号损伤小，相应代算法具有良好的收敛性能。

［1］PEI S C，T SENG C C.Complex adaptive IIR notch filter algorithm and its applications［J］.Circuits and SystemsⅡ:IEEE Transactions on Analog and Digital Signal Processing，1994，41(2):158－163.

［2］KO C C，LI C P.An adaptive IIR structure for the separation，enhancement，and t racking of multiple sinusoids［J］.IEEE Transactions on Signal Processing，1994，42(10):2832－2834.

［3］ 王勇，田斌，向新，等.一种应用于限制零极点位置复数陷波器的迭代算法［J］.信号处理，2007(1):6－9..

［4］ 炎晓蕊，李刚强，王勇，等.一种复数IIR自适应陷波器及其在QPSK扩频通信中的应用［J］.信号处理，2003，19(增刊):285－288.

［5］NISHIMURA S，HAL YUN J.Cascaded realization of complex adaptive IIR notch filters［EB/OL］.(2004－8－21)［2013－04－6］www.ieeexplore.ieee.org.

［6］NISHIMURA S，HAI－YUN J.Convergence analysis of complex adaptive IIR notch filters［EB/OL］.(2004－08－22)［2013－04－06］http://ieeexplore.ieee.org.

［7］MVUMA A，HINAMOTO T，NISHIMURA S.Gradientbased algorithms for a complex coefficient adaptive IIR notch filter steady－state analysis and application［EB/OL］.(2004－08－20)［2013－04－06］http://ieeexplore.ieee.org.

［8］STOICA P，NEHORAI A.Performance analysis of an adaptive notch filter with constrained poles and zeros［J］.IEEE Transaction on Signal Processing，1988，36(6):911.

［9］ 陈开周.最优化计算方法［M］.西安:西北电讯工程学院出版社，1984.

［10］李廷锋.求解大规模无约束优化问题的修正L－BFGS方法［D］.开封:河南大学，2008.