基于二人零和博弈的商业竞争模式分析

2013-04-25徐富盛尚绪凤许丁丁

电子科技 2013年11期

徐富盛，尚绪凤，许丁丁，吴芳

(中国计量学院理学院，浙江杭州310018)

随着互联网作用的日益增大。在互联网发展下的社交网络成为大众获取新闻消息的主要途径之一。正是由于社交网络的传播范围广、使用人数多，成为了商家推广产品的平台。文献［1］从传播学的角度，依据已存在的各类社交网站的生存状况，对中国社交网站的商业模式进行了定性研究。文献［2］也从传播学的角度出发，着重研究了SNS上的广告机制。

二人零和博弈是现实生活中常见的博弈形式，也是博弈论发展早期数学家特别感兴趣的一类博弈模型［3］。利用等分量线及支付凸多边形这两个基本概念，以图解方式确定简单二人零和博弈(2×n或m×2)的纳什均衡，确定持有多个纯策略局中人的均衡策略［4］。基于灰色系统理论的思想提出了二人有限零和灰色博弈的概念，利用分析技巧，建立了博弈平衡解优序关系的确定方法［5］。基于二人零和矩阵博弈给出了兵力分配优化模型［6］。针对二人静态博弈的基本结构，通过一般性的分析，给出了81种均衡实现的一般条件以及4种囚徒困境产生的基本条件［7］。基于博弈理论，对于分配到手术室的手术排程问题建立两人零和博弈模型，通过对这个模型的求解，得到手术的综合评价值。

本文基于二人零和有限博弈的思想，考虑社交平台信息的实际传播机理，以文献［8］中的公司竞争为例，分析这两家公司在社交平台的商业竞争模式。

1 社交网络的结构及蒲公英式传播

1.1 社交网络的基本结构

社交网络即社交网络服务［9］(Social Network Service，SNS)是指人和人之间通过朋友、血缘、交易、网络链接、理想、兴趣爱好等关系建立起来的社会网络结构。其包括用户、内容、社会网络和工具。用户，也称为网络中的节点;内容，即为用户运用该社交网络传播的内容;社交网络，即为关系，是节点与节点之间的连接，表示两节点相互认识，或者有相同的兴趣和属性等;工具，即为用于传播内容的载体。在网络中，人和人之间通过Blog、点评、群组等功能为网络用户进行“画像”，当这种“画像”越贴近现实中人的社会性，网络的社会化程度就越高。

1.2 社交网络中信息蒲公英式的传播

社交网络摆脱了门户网站时代以内容为中心的传播模式，以用户为主导，呈现出不同于传统网络信息传播的个性化、多元化、互动化的传播特征。社交网络中的信息传播方式包含有“中心式”传播、“单(多)关键点式”传播、“链式”传播、“蒲公英式”传播等［10］。

在实际的传播中，传播路径往往随着时间的推移不断变化，在各个传播模式之间进行着动态转换。“中心式”传播很容易变成“关键点”传播，而“链式”传播经常会变成“蒲公英式”传播。本文也仅讨论信息的蒲公英式传播。信息在社交网络中的蒲公英式传播，是一种结合“中心式”和“关键点式”的较为复杂的传播模式，这些承载信息的节点本身有一定的传播力，同时在2次或者3次转发中，又有很多关键节点帮助传播，最后常常能达到几千甚至上万的转发量。其传播图如图1所示。

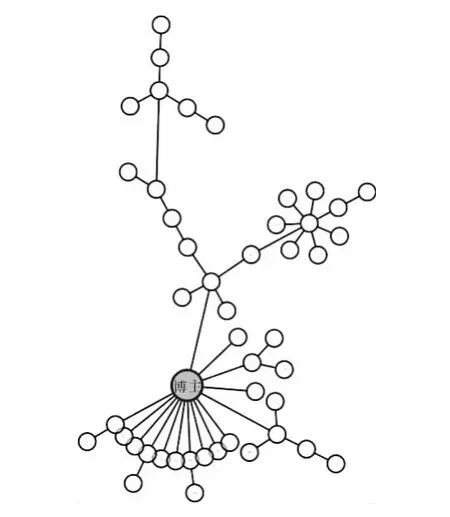
图1 社交网络中信息的“蒲公英式”传播图

2 二人零和有限博弈概念

二人零和有限博弈:即甲与乙利益冲突，一方的收益就是对方的损失。假设甲的策略集X={x1，x2，…，xm};乙的策略集Y={y1，y2，…，yn}。令S=X×Y={(xi，yj):=1，2，…，m;j=1，2，…，n}，甲、乙的收益函数分别为f∶S→R;g∶S→R，则f(xi，yj)+g(xi，yj)=0(i=1，2，…，m;j=1，2，…，n)即甲所得收益是乙损失的［8］。但若在一策略组合中，两个参与者面临一种情况，当其他人不改变策略时，他此时的策略是最好的，那么此时博弈到达一个平衡，称为纳什均衡。也就是说，此时如果他改变策略其收益将会降低。在纳什均衡点上，每一个理性的参与者都不会有单独改变策略的冲动。纳什均衡点存在性证明的前提是“博弈均衡偶”概念的提出。而“均衡偶”是在二人零和博弈中，当局中人A采取其最优策略a*，局中人B也采取其最优策略b*，如果局中人B仍采取b*，而局中人A却采取另一种策略a，那么局中人A的收益不会超过他采取原来的策略a*的收益。这一结果对局中人B亦是如此。

3 模型的假设

(1)社交网络上有两种推广者进行产品的网络推广，分别为专业推广者和兼职推广者，且兼职推广者需要经过专业推广者培训才能工作。(2)两家公司推广产品的资金均为M元。(3)兼职推广者的日薪为s元，且每天每人所能推广的人数为p人。(4)专业推广者的人数有限，为z人，日薪不定，可随时转投工资更高的公司，每天每人所能推广的人数为P人，且每天每人最多可以培训兼职推广者J人。

4 模型的建立

4.1 专业推广者的最高日薪

根据假设，专业推广者的人数有限，那么专业推广者的人数多少就意味着推广效果的好坏。但专业推广者的工资不可能无限增长，公司也必定存在一个可接受的最大值。而无论专业推广者的工资多少，他每天能吸引粉丝的数量为固定的P人，兼职推广者日薪s元，他每天能吸引粉丝的数量为p人。对于两个理性的公司而言，便会考虑专业推广者和兼职推广者的价值，即专业推广者的粉丝效益与兼职者的粉丝效益。显然当两者的价值相同时，专业推广者的日薪存在着上限值S

由式(1)便可以得到专业推广者的最高日薪。

4.2 资金使用和用人方案的模型

根据二人零和博弈的特点，由于公司若只是在前期对产品进行推广，那么随着时间的推移，接触产品的人会对产品的印象降低，达不到预期的效果。因而本文在此假设两个公司尽力推广产品的时间为D天，且公司拥有相同的资金。由纳什均衡原理，容易得出两个公司将会对产品的推广给出一样的预算方案，既而可得到两个公司分别得到专业推广者z/2人。

兼职推广者的分批培训完和一天培训完是一样的，那么考虑将需要数量的兼职推广者在同一天培训完，而后便由这些兼职推广者来推广，不需要专业推广者。由于现在要推广D天，也就是说每天公司平均所付出的工资不能超过M/D元，那么容易得到每天兼职推广者人数不超过M/(D×s)个。

考虑推广效益转化为直接粉丝量最大。故得到如下等式:目标函数为推广期间总的直接粉丝量Z

式中，mi表示第i天每位专业推广者培训学员的人数;ai为第i天培训人员的专业推广者;bi为第i天网络推广的专业推广者人数。

每天雇佣专业推广者人数ci不超过m/2

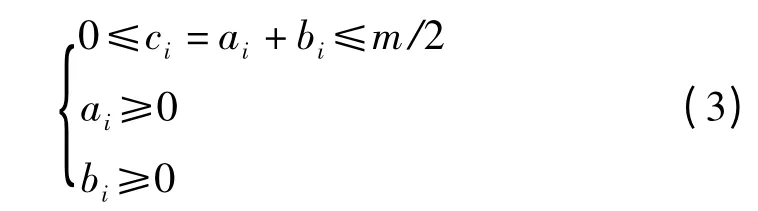
每天每个专业推广者培训学员的人数mi不超过J

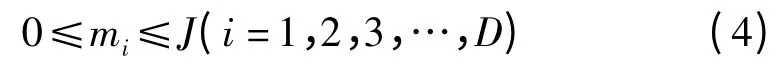
总推广费用不超过M元

由此可得以直接粉丝量为单目标的线性优化模型

5 仿真求解

对于上述的线性规划模型，当各个变量取如下值:D=100;m=10;s=50;p=35;P=500;M=200 000;J=20。

即当两个公司拥有20万的推广资金，市场仅有10名专业推广者，且每个推广者每天能固定增多500个粉丝，每天能培训最多20个兼职推广者，且推广者的日薪为35元，其每天能固定增多的粉丝为50个。在持续推广100天的情况下，运用Lingo软件求解得到最终直接粉丝量为138 600，如图2所示。第1天，聘请2名专业推广者去培训40名学员，后99天每天由这40名兼职推广者去做网络推广，剩余资金571.4元。由于Lingo求解得到的是全局最优解，对其结果进行了分析，得到结果如表1所示。

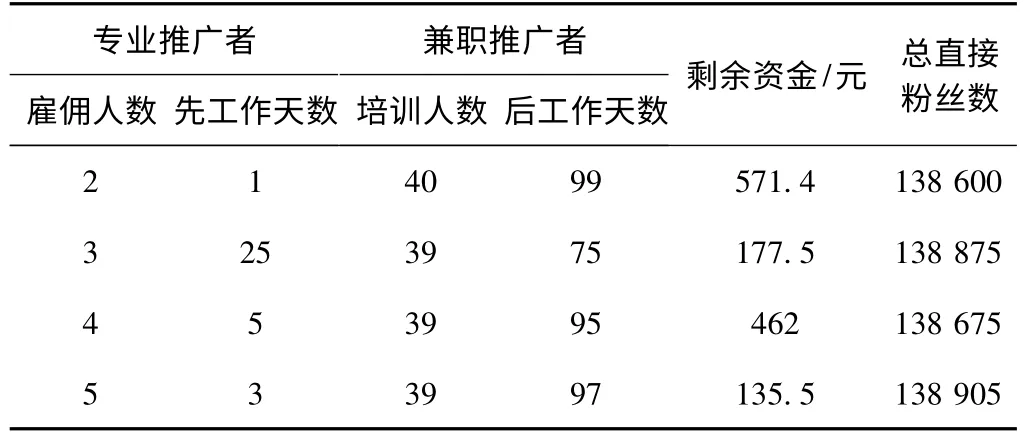
表1 公司的分配方案和总直接粉丝数

图2 Lingo求解结果

6 模型的检验

由上述的结论，易知剩余资金过多，显然不是公司所希望的。故而本文在此对上述的结论进行分析和调整。由表1中可以看出雇佣专业推广者人数为5的方案最优。即得到最优的资金使用和用人方案如下:用人方案:前2天雇佣5名专业推广都做网络推广，第3天其中3名继续做网络推广，另外2名去培训39名学员，后97天只由这39名兼职推广者去做网络推广，不再雇佣专业推广者。剩余的费用:135.5元。此时总直接粉丝量:138 905人。