基于矢量网络分析仪实现微波器件的群时延测量

2013-04-24卢娟李智

计量技术 2013年7期

卢娟李智

(深圳市计量质量检测研究院，深圳 518055)

0 引言

群时延是指群信号通过线性系统或网络传播时，系统对信号整体产生的时延，是系统的重要指标之一。如何进行快捷、精密的群时延测量一直是测量领域的难点和热点。本文论述的方法是通过一台矢量网络分析仪完成对微波器件精密群时延测量的全过程。首先通过理论推导，建立了矢量网络分析仪S21相位测量值与整个系统群时延之间的数学联系，然后，结合实验来验证其方法和测量结果的正确性。

1 矢量网络分析仪测量群时延的原理

群时延数学表达式为：

(1)

式中，tg(ω)为群时延(s)；φ为相移(°)；ω为角频率(°/s)。

矢量网络分析仪可以测量二端口网络之间的相移。图1所示为一接有信号源bg和负载ZL的二端口网络，Γg和ΓL分别为信号源和负载的反射系数，a1和b1分别是二端口网络端口1入射波和出射波的复数波幅，a2和b2分别是二端口网络端口2入射波和出射波的复数波幅。其中在一般情况下，二端口网络的相移即为b2和a1之间的相位差。

图1 二端口网络的相移

图2 二端口网络相移的信号流图

那么整个系统的信号流图如图2所示。S11、S21、S12和S22分别为二端口网络的散射参数。由流图很容易得到：

(2)

(3)

则由式(2)和式(3)可以得到相移φ为：

(4)

当信号源匹配，Γg=0，则式(4)变为：

(5)

若信号源匹配，而且二端口网络输出端接有匹配负载，即ΓL=0，则式(5)变为：

φ=arg(S21)

(6)

从式(4)和式(6)可以看出二端口相移的测量结果主要与散射参数S21有关，也与两端口网络的其他散射参数及相连接的源和负载的反射有关。而由式(1)可知相移和时延有必然的联系，因此，用经过校准的网络分析仪上测量S21可以得到整个系统的群时延。

由于ω=360°×f，代入式(1)，得到：

(7)

当频率差Δf很小时，系统地群时延可以近似地表示为：

(8)

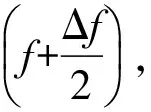
由式(8)可得，群时延测量不确定度为：

(9)

式中，Δf常被称为孔径，其取值大小是否合理关系到群时延测量精度高低和分辨力大小，也关系到测量结果是否有意义。Δf的选取需遵循三条原则：

1)根据信号频率和系统带宽选择合适的Δf。根据式(8)可知，Δf越小测量越真实。

2)根据时延测量准确度和分辨力要求选择Δf。根据式(9)可知，Δf越大测量准确度越高。

3)根据被测时延值来选择Δf。根据式(8)，群时延的最大值为：

(10)

为了使群时延测量结果不产生模糊，tgmax应该大于被测群时延tg(f)，即：

(11)

由式(11)可以得到：

(12)

2 应用矢量网络分析仪的时延测量实验

我们用经过校准的网络分析仪对美国TELEDYNE公司的延迟线MBG-1152进行群时延测量。选取网络分析仪为Agilent PNA E8358，校准件为Agilent 85052D。

被测延迟线MBG-1152在中心频率4.3GHz处的标称时延为tgref=1.016μs。将tgref代入式(12)，可知Δf<0.98MHz。设置网络分析仪中心频率在4.3GHz，频带宽度为10MHz，测试点数为201，此时Δf约为50kHz。网络分析仪进行完全二端口校准后，将延迟线的两端分别接在网络分析仪的两个端口之间，选择S21测量delay的功能，可以看到延迟线MBG-1152的时延基本上为一条直线，在4.3GHz频率处重复测量10次，取平均值，得到群时延测量结果tg=1.014μs，测量误差Δtg=-2ns。

此次测量的不确定度主要来源于重复测量，网络分析仪本身的相位测量误差和系统相位扫迹噪声。

重复测量引入的不确定度分量为：

u1(tg)=3.8ns