基于Delta-Sigma调制技术的谐波信号源的设计与仿真*
2013-04-24尼佳伟王文理谢振山
尼佳伟 王 磊 王文理 谢振山
(1.河北大学,保定 071002;2.中国计量科学研究院,北京 100013)
0 引言
Delta-Sigma调制器具有独特的过采样技术和噪声整形技术,所谓过采样技术就是以远高于奈奎斯特采样频率的频率对模拟信号进行采样,噪声整形就是将低频段的量化噪声转移到高频段,从而减小信号基带内的量化噪声,提高输出信噪比,高频噪声可通过低通滤波器滤除。采用Delta-sigma调制器可以很好的提高信号的信噪比及准确度。目前Delta-Sigma调制在D类放大器中已得到深入研究和广泛应用[1]。
本文目标就是设计一种谐波信号源,该谐波信号源基于D类放大器,并通过采用一些先进的电路结构,使其达到SNR不低于90dB,幅度放大倍数不小于100。其总体结构是首先通过一个5阶的CIFB结构的Delta-Sigma调制器将所需放大的信号调制成1bit的数据流,将其作为全桥电路的开关信号,利用全桥放大电路将Delta-Sigma调制波进行放大,最后经过一个低通滤波器还原信号。
1 系统设计
1.1 Delta-Sigma调制器设计
Delta-Sigma调制器的信噪比(SNR)是由电路的过采样率(OSR)和噪声整形的阶数共同决定的。为了提高Delta-Sigma的信噪比及其THD,可以通过提高噪声整形的阶数来提高调制器的性能。CIFB结构的调制器通过引入输入信号前馈至量化器直接处理,可以有效的提高信噪比。
图1所示为一个5阶CIFB的Delta-Sigma调制器的结构,包含5个积分器、5级输出信号反馈、6级输入信号前置反馈和一个单位量化器,ai、bi为反馈系数。
当ai=bi(i≤5)且a6=1时,系统的传递函数STF(z)=1,噪声传递函数为:
NTF(z) =1/[b1(Iz)5+b2(Iz)4+b3(Iz)3+b4(Iz)2
+b5(Iz)1+1]
(1)
式中Iz=z-1/(1-z-1)为积分器传递函数。
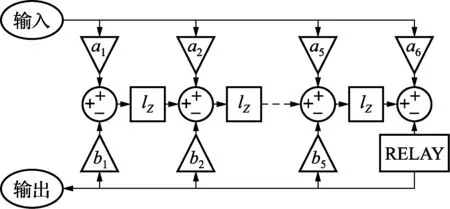
图1 5阶CIFB的Delta-Sigma调制器
调制器的输出Y(z)为:
Y(z)=X(z)+NTF(z)E(z)
(2)
其中,X(z)为系统输入;E(z)为量化噪声。
考虑结构中第i(i≥2)级积分器输入Ui(z):
Ui(z) =Ui-1(z)Iz+aiX(z)-biY(z)
=Ui-1(z)Iz-biNTF(z)E(z)
(3)
而第一级积分器的输入为:
U1(z)=aiX(z)-bjY(z)=-biNTF(z)E(z)
(4)
结合式(3)和式(4)可知,环路中积分器的输入信号中只含有量化噪声量,而不含初始输入信号量,即积分器只处理环路中的量化噪声,不处理初始输入信号,初始输入信号通过前置反馈直接送至量化器处理,避免了积分器非理想因素的影响,具有低失真的特点。[2]
利用由Richard Schreier提供的Matlab工具箱Delta Sigma Toolbox来计算我们所需的反馈系统,调制器的阶数为5,采样率为128,采用CIFB结构,经计算可得反馈系数的具体设计值如表1所示。

表1Delta-Sigma调制器参数设置
1.2 滤波器设计
本谐波源要能够生成2~100次的谐波,通带频率需要达到50×100=5kHz。当5阶CIFB结构的Delta-Sigma调制器的输入是幅度为0.5的100次谐波,输出频谱如图2所示。
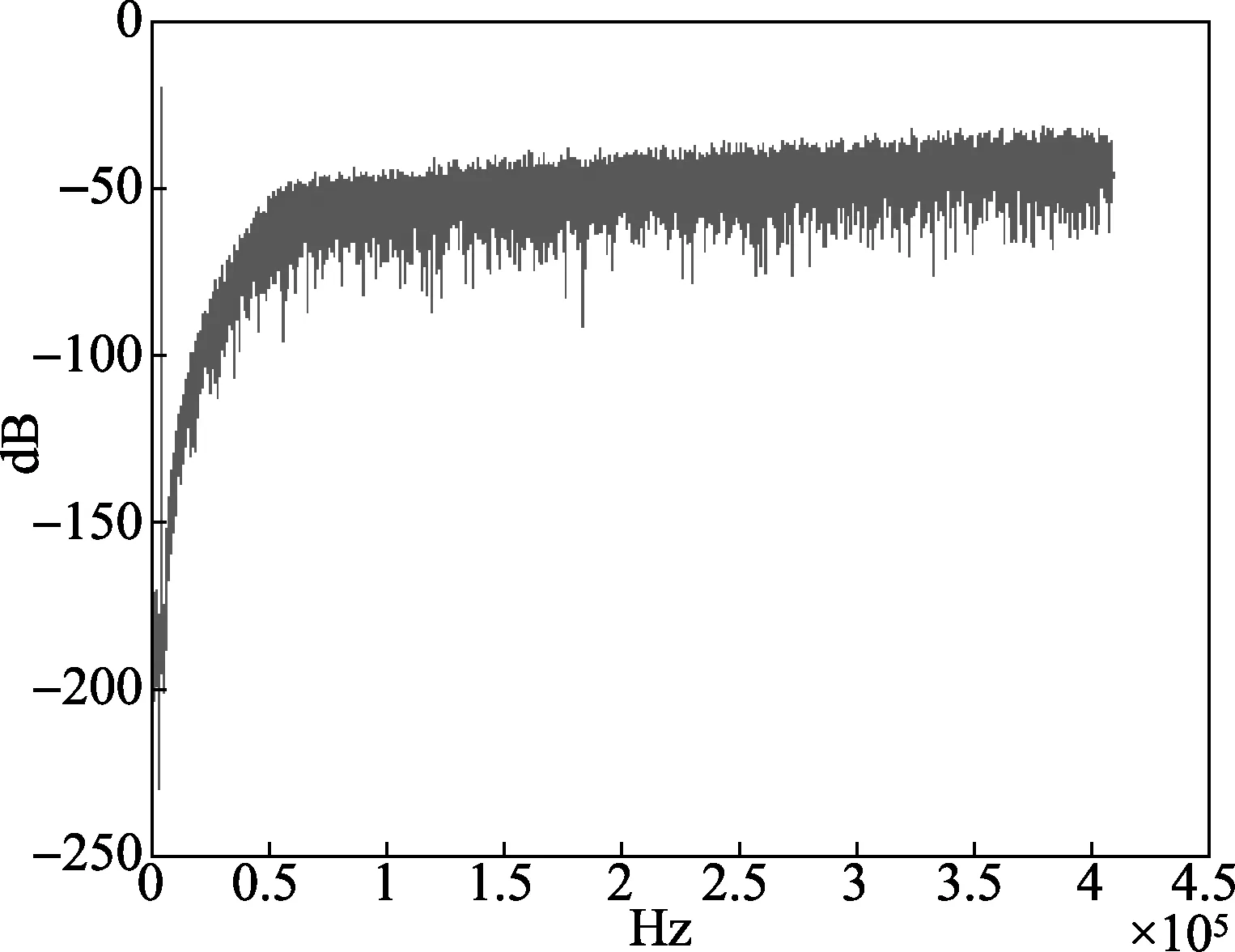
图2 Delta-Sigma调制器输出频谱
为了良好的频率响应,低通滤波器的截止频率不应低于5kHz,为了更好的滤去高频噪声,滤波器在30kHz时,幅值应降低100dB。利用软件进行LC低通滤波器设计[3]。常用的低通滤波器有巴特沃斯型、切比雪夫型和椭圆函数型。其中椭圆函数型滤波器具有最窄的过渡带。利用专业滤波器设计软件Filter Solution进行滤波器辅助设计,将滤波器通带宽度Fp设为5.5kHz,通带波动为0.001dB。若想在30kHz时,阻带衰减达到-100dB,可以利用软件计算出巴特沃斯型、切比雪夫型和椭圆函数型分别需要7阶、7阶和6阶。椭圆函数滤波器所需阶数最少,电路形式会相对简单。当采用50 Ω负载时,低通滤波器构成如图3所示。其中L1=1.651mH,L3=1.764mH,L5=1.024mH,C2=762.3nF,C3=14.82nF,C4=600.1nF,C5=600.1nF,C6=142.6nF。低通滤波器的幅频特性如图4所示。
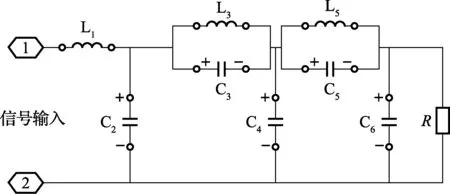
图3 6阶椭圆函数低通滤波器
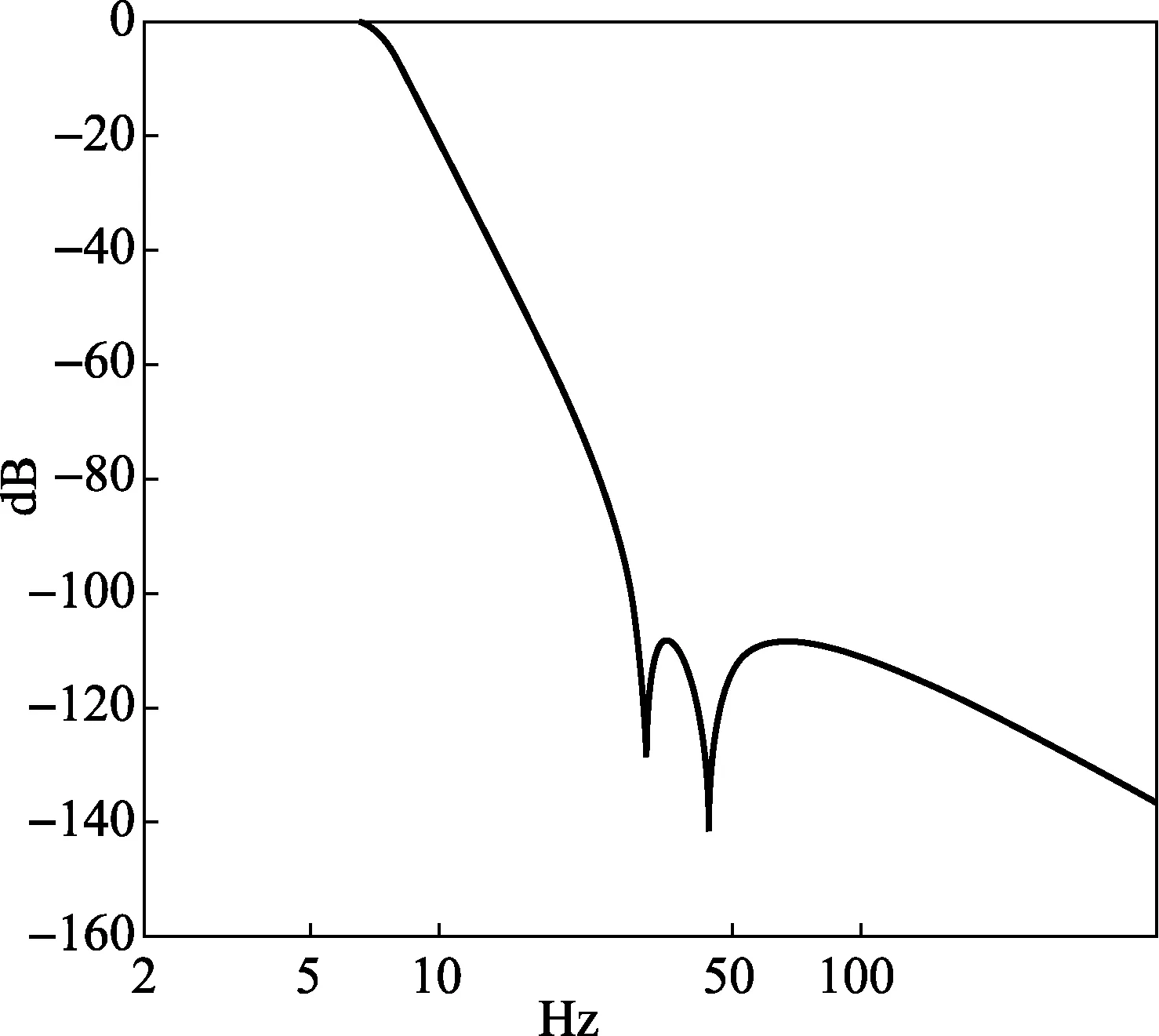
图4 滤波器幅频特性
使用6阶椭圆滤波器的传递函数为:
(5)
将传递函数导入Matlab,通过双线性变换将模拟低通滤波器转换为数字低通滤波器[4],可以使用Matlab对其进行仿真。Delta-Sigma调制波经滤波后的信号进行fft分析可得其频谱如图5所示。由图5可知,高频信号的幅值降为-150 dB左右,高频信号被很好的滤除。
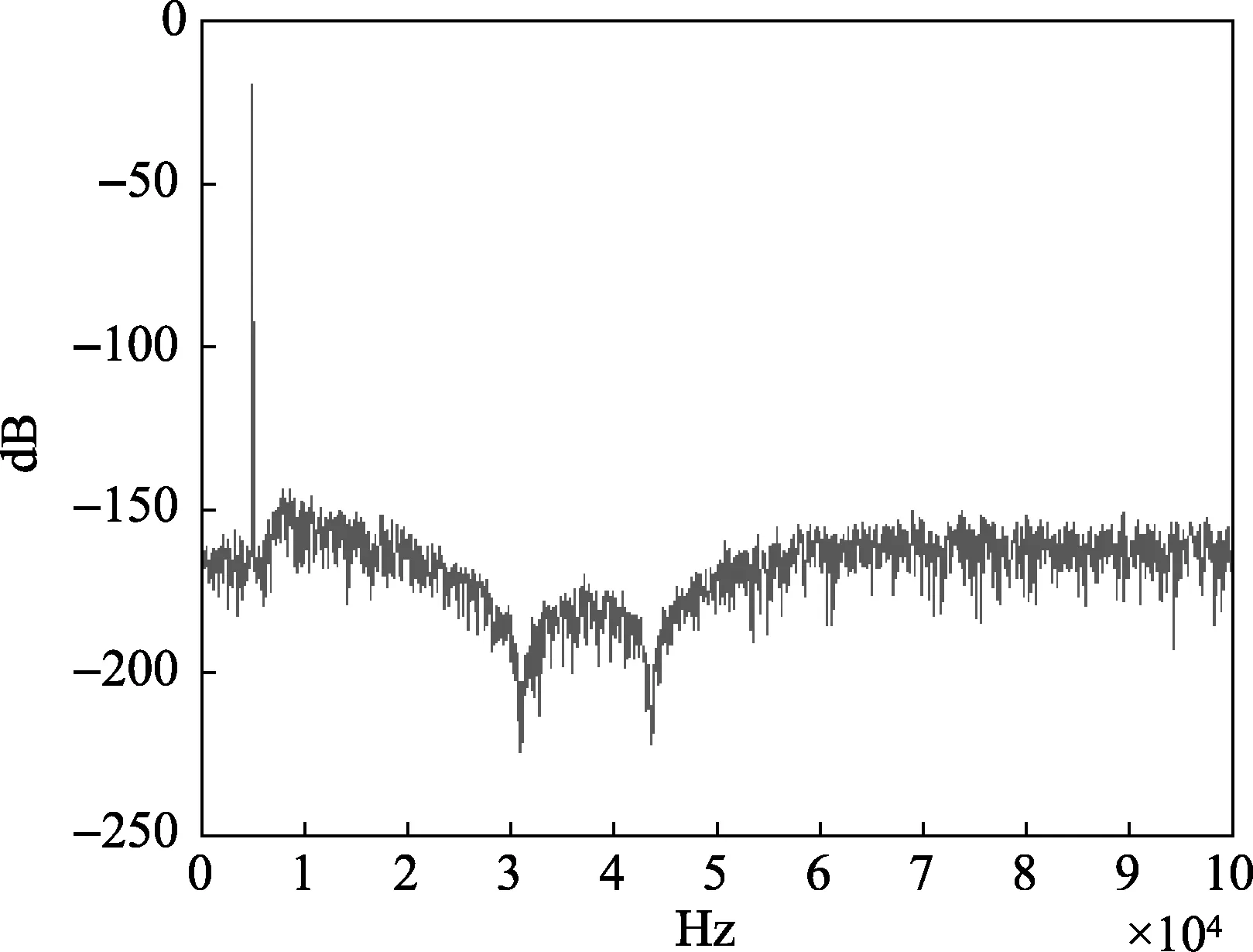
图5 滤波后频谱图
2 系统仿真
2.1 理想系统仿真
系统由Delta-Sigma调制器,全桥放大器及滤波器构成。全桥放大电路的直流电源采用100V的电压源。Delta-Sigma调制器的输出经过全桥放大电路后将被放大为幅度100V的Delta-Sigma调制波,放大倍数为100。经过低通滤波器后,还原为经过100倍放大的输入信号。
当输入信号的幅度为0.5,频率分别为2次谐波(100Hz)以及100次谐波(5kHz)即输入信号为0.5sin(200p t)和0.5sin(10000pt)时,通过Matlab的计算可得系统的SNR及THD如表2所示。
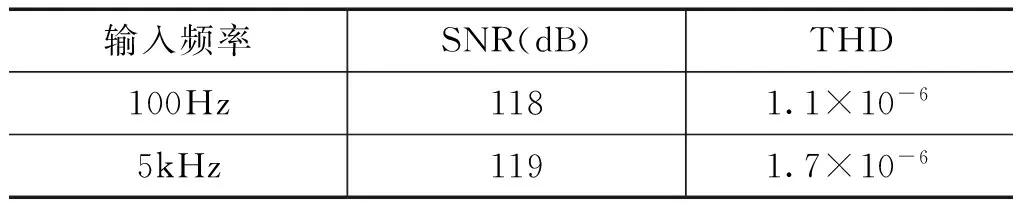
表2系统SNR及THD
由表2可以得知,在理想条件下,系统输出的THD很小,信噪比能够达到118dB。当2次谐波和100次谐波的输入幅度均为0.1、0.2、0.3、0.4和0.5时,其输出幅值分别如表3和表4所示。
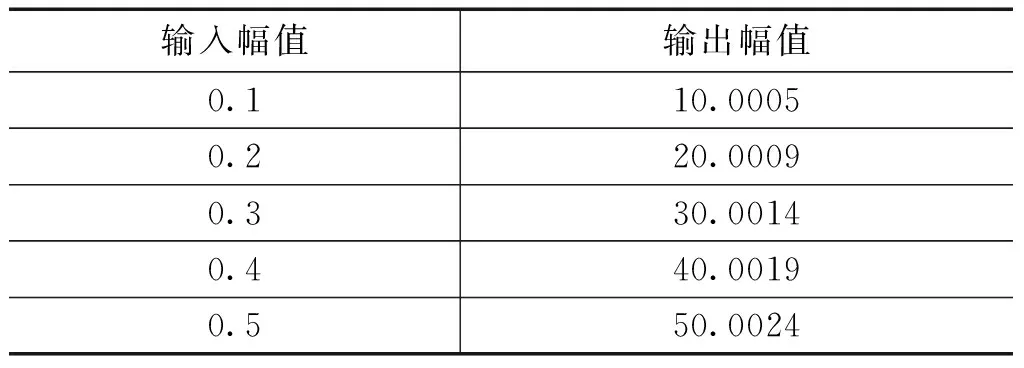
表32次谐波的输出幅值
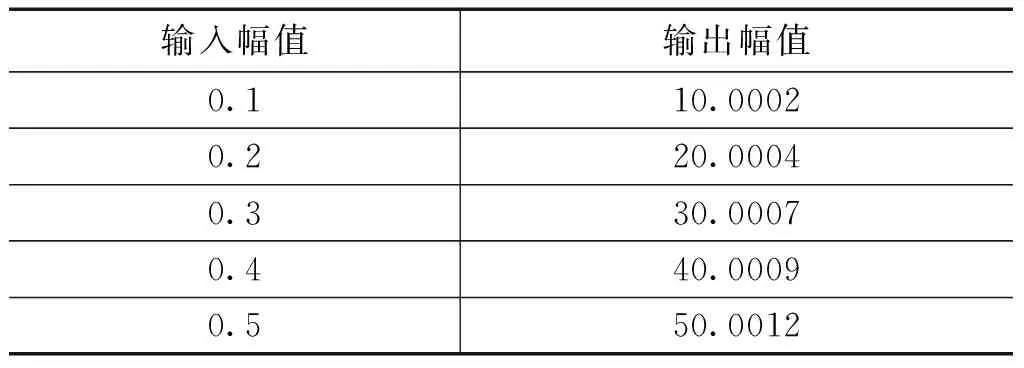
表4100次谐波的输出幅值
由表3和表4可以算出系统的输出准确度能够达到0.001%。系统分辨力可以到达19 bit。而表3和表4中的输出值明显低于19 bit的准确度。其原因在于本系统所采用的滤波器在通带内有0.001 dB的幅值波动,实际输出值与理想输出值的比值0.9999,会有0.01%的偏差。表3与表4中数据的偏差均小于0.01%。
2.2 电源纹波的影响
纹波是由于直流稳定电源的电压波动而造成的一种现象,因为直流稳定电源一般是由交流电源经整流稳压等环节而形成的,这就不可避免地在直流稳定量中多少带有一些纹波。我们在直流电源上叠加一个频率为f=50Hz的纹波Ur。
Ur=mag·sin(2pft)
(6)
式中,mag为幅度,它的取值分别为100V的1%、0.5%、0.1%、0.05%、0.01%和0.001%的正弦波信号。输入为0.5sin(200pt)。仿真结果如表5所示。
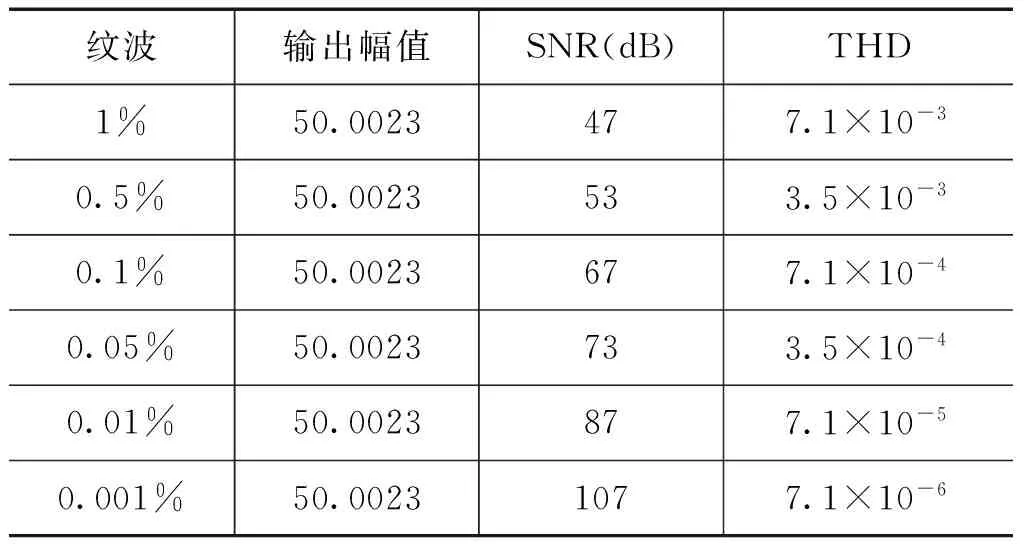
表5电源谐波的影响
由表5可知,直流电源纹波对系统的SNR和THD有着极大的影响,若要使系统的SNR不低于85dB,直流源的纹波幅值不能大于0.01%。
2.3 死区对系统的影响
图6为一全桥电路结构,它由四个开关管(k1、k2、k3和k4)构成。KG1和KG2为开关信号。LPF采用图3所示滤波器结构,将其作为全桥电路的负载,Vcc为全桥电路提供直流电压。
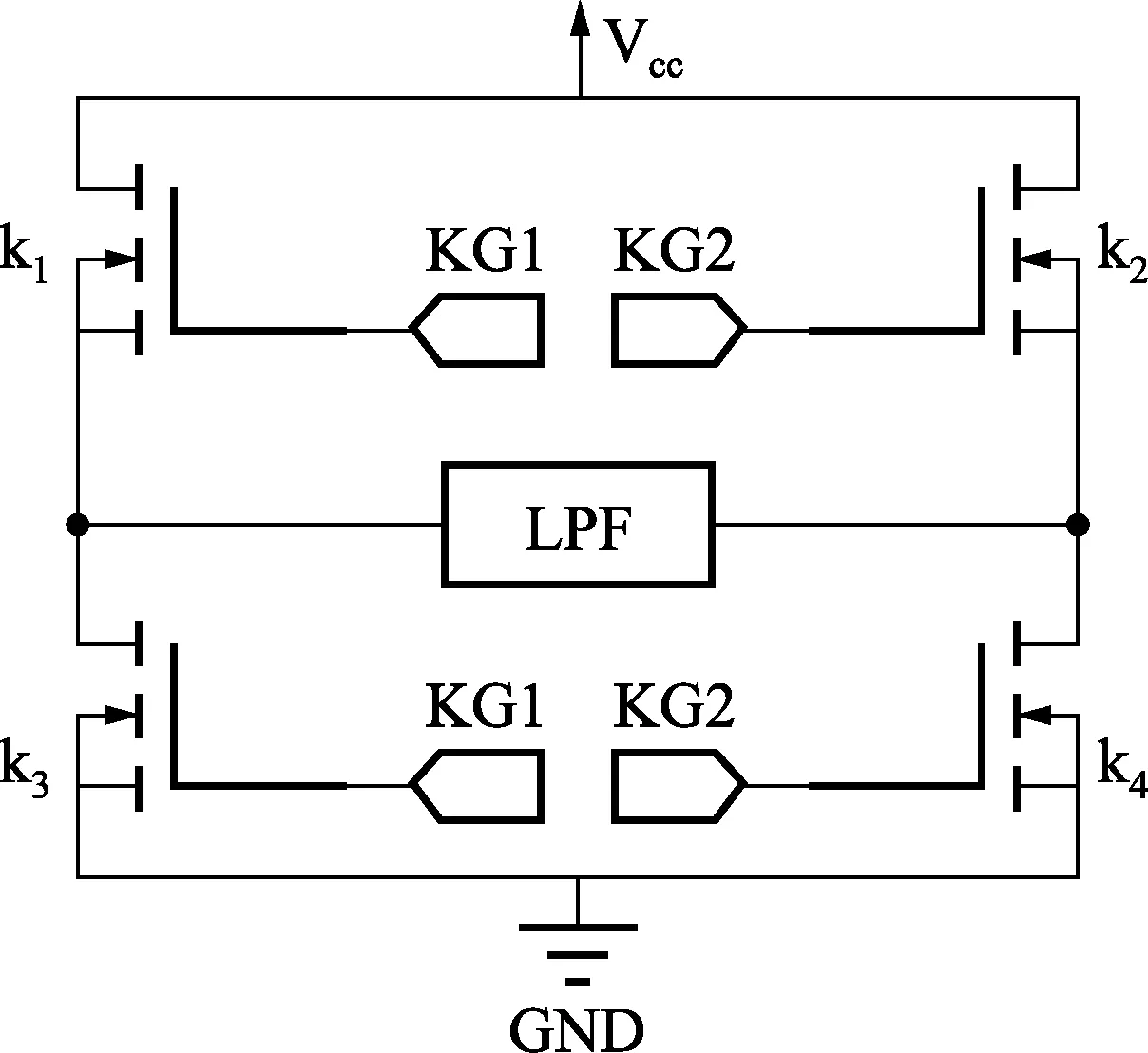
图6 全桥电路结构
两个桥臂在Delta-Sigma调制波的作用下交替打开。由于全桥电路不可能由完全理想的开关构成,每个桥臂的打开和关闭会有一定的延迟,而导通的MOSFET的漏源电阻极小。在开关信号切换的瞬间,会出现电源到地的短暂低阻导通,对系统会造成极大的危害。为了避免这种短暂的低阻导通,需要引入死区时间[4],死区时间td如图7所示。
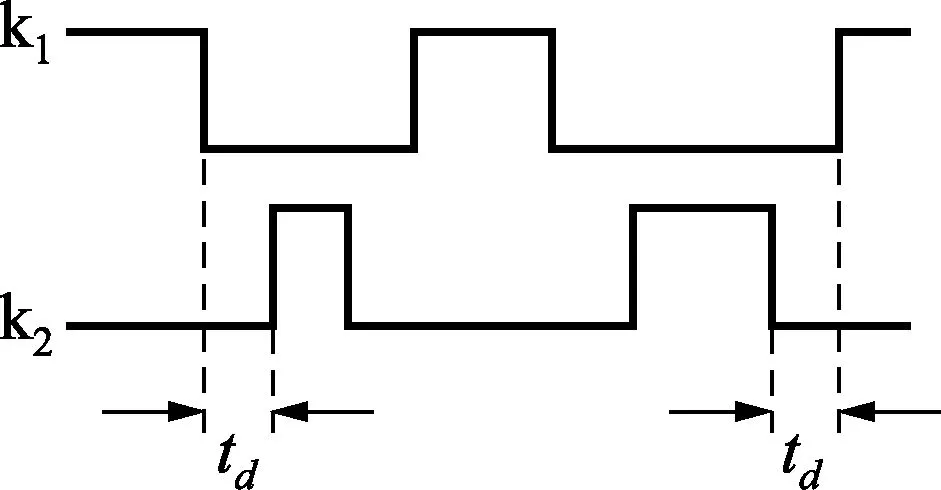
图7 死区时间
在KG1和KG2开关信号切换的瞬间,对KG2增加一个20ns的死区时间。
表6列举了不同死区时间对系统输出幅值的影响。当死区时间为20ns时,与无死区时间相比,输出幅值降低3.29%。随着死区时间的增大,输出幅值持续下降,输出幅值的的准确度明显变差。
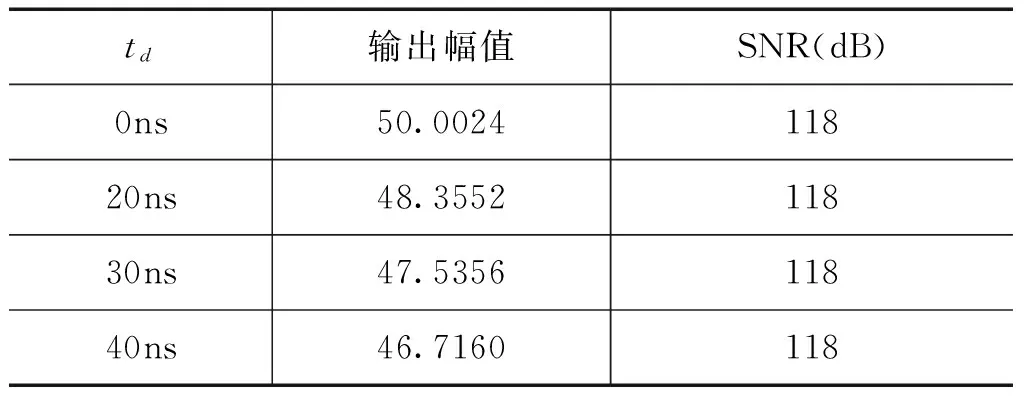
表6死区影响
当死区时间为20ns,输入幅值分别为0.1、0.2、0.3、0.4和0.5时,输出结果如表7所示。通过对表7中的数据进行计算可以发现,不同的输入幅值在20ns死区时间所产生输出误差均为3.29%。当死区时间为40ns时,同样进行上述过程,可得表8。对表8中的数据进行计算,不同的输入幅值在40ns死区时间下所产生输出误差均为6.57%。由此可知,死区对系统输出幅值误差的影响是一定的,通过仿真得出不同死区所引起的误差值,在系统中添加适当的补偿,就可以消除死区对输出的影响。
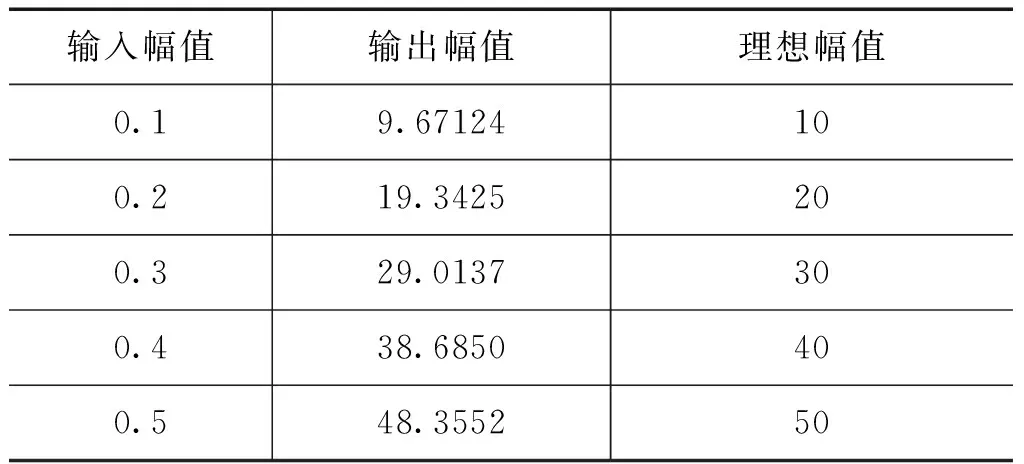
表720ns死区时间
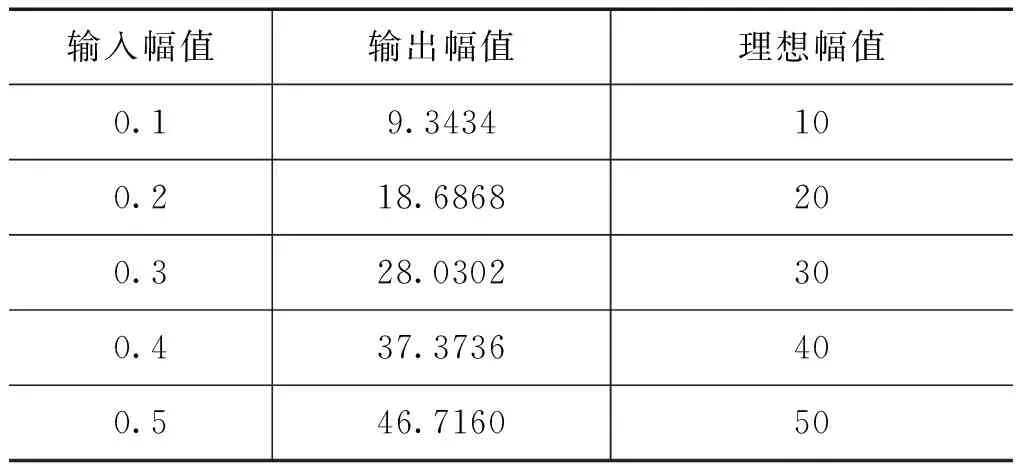
表840ns死区时间
3 结论
本文介绍了一种基于Delta-Sigma调制技术的谐波信号源的基本结构,并通过Matlab对其进行了建模与仿真。通过构造一种5阶CIFB结构的Delta-Sigma调制器和低通滤波器滤波电路,本文所设计谐波信号源在电源纹波幅值不大于0.01%的情况下,信噪比可达到87 dB。由于电源纹波对系统的SNR有着极大的影响,为了提高系统的SNR,应该选用纹波系数极低的直流电源并且应该增加滤波用的电感和电容来抑制纹波。为了改善死区时间对系统的影响,在实际系统设计中应当引入死区补偿环节以改善系统性能。
[1] 高爱国.基于MATLAB的D类功率放大器的仿真分析[J].电子科技,2012,25(5)
[2] 苏小波,柴旭朝,戴 欢,顾晓峰,于宗光.用于MEMS传感器的三阶Σ-Δ调制器设计[J].微电子学,2010,40(5)
[3] Arthur B.Williams,Fred J.taylor.宁彦卿,姚金科,译.电子滤波器设计[M].北京:科学出版社,2008
[4] Vinay K.Ingle,John G.Proakis.刘树棠,译.数字信号处理(MATLAB版)[M].西安:西安交通大学出版社,2008
[5] 刘冬蒨.新型D类音频功率放大器设计[D].北京交通大学,2009
