基于模糊神经网络的数字资源服务绩效评价研究

朱世伟，鞠镁隆，于俊凤，魏墨济，王蕾

(山东省科学院情报研究所，山东 济南 250014)

数字资源(电子资源)是被设计用来存储海量的结构化或者半结构化数据的元数据仓储。近年来，随着对数字图书馆和电子资源投入日渐加大，进行数字资源绩效评估的需求也更加迫切［1］。需要开发相关的绩效评价模型来对电子资源的使用绩效进行评估。

美国图书馆界在20世纪60年代后期把在企业管理界应用广泛的绩效评价方法引入到图书馆的服务绩效评价中［2］。经过近半个世纪的发展，相关专家学者对图书馆服务绩效评价的概念和内涵已经达成了部分共识:图书馆的绩效评价，就是按照给定的标准和要求，设定一定的指标，利用科学评价方法和模型，对一定资金和其它资源投入的图书馆在一定时间内的产出和服务进行评价和测试［3］，也就是说，对图书馆在一定投入资本下的产出效益进行评估和比较。

1 相关研究综述

20世纪90年代中后期，以英美发达国家为首的部分国家和地区发起了一些针对数字图书馆服务绩效进行评估的项目，并由此建立了一些绩效评价的标准和指南。主要有:(1)美国图书馆研究协会发起的“ARL电子图书馆服务评价(E-METRICS)”项目［4－5］对数字图书馆数字资源的服务绩效的评估进行了研究和分析，提出了一套数字资源绩效评价的指标体系，该体系共包含14个数字资源绩效评价指标;(2)网络电子资源在线使用统计(COUNTER)项目［6］设定了4大类数字资源使用的规范和准则。截至目前，COUNTER已经成为了数字图书馆绩效评估方面的国际通用标准和规范;(3)欧洲图书馆绩效评价和质量管理系统EQUINOX项目从5个方面设定了14个指标对数字资源服务绩效进行评价［7］;(4)网络环境中国家公共图书馆统计和绩效测度项目出版了《公共图书馆网络化服务统计和绩效测度》手册，提出了一整套对公共图书馆数字资源和服务进行评价的统计指标体系［7］。

国内的相关研究多数都是独立进行的，几乎没有相关的学术团体或者部门对该类项目的开展进行任何形式的资助。索传军等［3］对电子资源在线使用统计进行了分析，指出数字资源绩效评价的主要目标是为了促进电子资源的标准化和易用性。黄颖［8］以用户感知为中心的图书馆绩效评价模型LibQUAL+TM为理论基础，进一步剖析了学术环境下的满意程度与服务质量的辨证关系，构建了一个以内部图书馆专家群体确定和外部终端用户群体感知为核心的、融合满意程度和服务质量的大学图书馆电子资源绩效评价理论模型。史继红［9］比较了EQUINOX项目和ARL E-Metrics项目的评价结果，提出了包括不同方法优缺点、指标选取原则等在内的一系列相关问题。

上述研究为数字资源建设做出了贡献，然而，当前国内的研究还存在两个弊端:一是国内学者开展的研究大多采用在国外广为使用的方法和模型，对国内高校或者公立图书馆的数字资源提供的服务进行绩效评价，却忽视了寻找符合我国实际情况的评价模型和指标体系的工作;二是部分学者虽然提出了自己独创的评价模型和方法，但是却没有进行实验分析和验证。本文提出了模糊神经网络(fuzzy neural network，FNN)评价模型，对高校和公立图书馆数字资源的使用绩效进行评价，并选取数据进行了实验验证。

2 模糊神经网络

2.1 模糊神经网络结构

模糊神经网络的结构如图1所示。为了简单说明，我们假定本文考虑的模糊神经网络具有多个输入和一个输出。模糊神经网络的结构为5层结构，推理规则采用Takagi-Sugeno模糊推理逻辑，推理规则为［10］:

其中，Rk是第k个规则(1≤k≤L)，L是规则的长度，x={xi}，i=1，…，n为输入向量，ωk是第 k个网络的连接参数［11］。是Gaussian核函数定义的模糊集合:

图1 模糊神经网络结构图Fig.1 Structure illustration of fuzzy neural network

其中 i=1，2，…，n，k=1，2，…，L，μik是 xi的成员函数，cik和σik分别是Gaussian核函数的中心和宽度，n是输入向量的数量，L是每个输入变量成员函数的数量［12－13］。

模糊神经网络各层实现的主要功能如下:

第一层:输入层，该层每一个节点代表一个输入向量;

第二层:模糊化层，该层的每一个节点被划分成L个组，每个组代表一个模糊规则的IF推理部分［14］。每一个节点都参与成员函数μik(xi)值的计算;

第三层:模糊推理层，该层的节点数目和模糊规则的数目相等，每个节点都参与计算第k个模糊规则Rk，其输出为:

第四层:归一化层，实现归一化计算。节点的数目与第三层节点数目相等［15］。Nk节点的输出为:

第五层:输出层，输出层只有一个节点，其输出y为:

其中，ωk是规则k的连接参数(连接权值)。

传统FNN输入变量的成员函数数量需要根据专家知识来确定。然而，不同的模糊系统之间的差别是显而易见的，因此，对于网络设计者来说，针对特定系统选择恰当的模糊规则数不是一件容易的事情。此外，固定结构的模糊神经网络在面对不同的数据集时的适应性也是一个不可回避的问题。模糊规则过多或者过少都将会对系统的分析造成难以避免的错误和问题［16］。本文中模糊规则数的确定采用了由Qiao［17］提出的一种自组织的算法来执行，该方法能够自动地按照实际问题的需求确定模糊规则数。

2.2 学习算法

模糊神经网络的自组织算法主要分为网络结构的设计和参数的优化训练两个步骤进行。每个阶段都假设数据集是由p个输入-输出对组成:

为给FNN选择合适的模糊规则数，我们在输入输出空间的划分中采用了聚类算法，利用改进的RPCL(Rival penalized competitive learning)［18］算法来获得紧凑的网络结构。聚类的数量在训练的过程中自动的获得，以此来获得可伸缩性的输入输出空间划分方法和优化的模糊规则数。然后，删除部分冗余节点和连接，产生最终优化的模糊神经网络结构。

网络结构确定以后，便进入优化学习阶段，该阶段将采用自组织学习阶段获得的参数初始化网络。参数的优化在相同的数据集合S上利用改进的反向传播算法(Back propagation algorithm)执行，以获得最终的最优网络模型［19］。

给定集合S中任意的输入xp，根据公式(1)～(4)，可以得到网络的输出为:

假设网络误差函数为:

其中，yp和是p维的网络输出值和期望输出值，可以得到:

从公式(8)可以计算得到:

同样的我们可以分别得到方差σik和权值ωk，计算公式分别如式(10)、(11)所示:

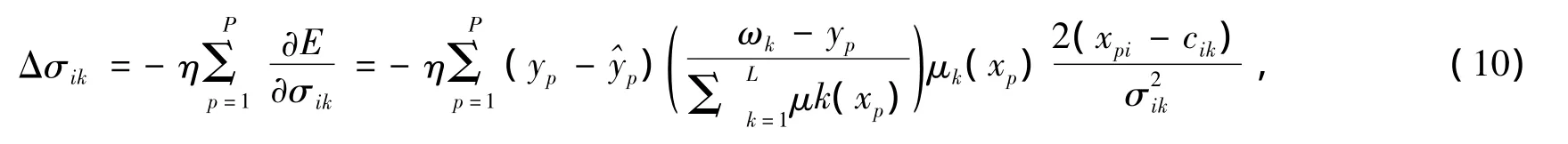
3 数字资源评价指标体系

3.1 评价指标选取

数字资源服务绩效评价系统是一个结构复杂的系统，包含特定的使用环境、服务条件和数字资源服务效益等诸多影响因素，因此，需要通过对数字资源的服务绩效在纵向和横向上进行比较，以此来确定最佳的评价指标，如此一来，便无形中提高了评价指标选取的难度。本文在评价指标的选取时，考虑借鉴美国国家信息标准化组织(NISO)颁布的《信息服务和使用:图书馆和信息服务机构统计指标——数据字典(ANSI/NISO Z39.7－2004)》标准，同时结合我国数字图书馆建设的实际状况，依据科学性与全面性、定量指标与定性指标、可比性与可操作性等原则相结合，构建了一套数字资源服务绩效评价的指标体系框架［3，6］。

综上所述，本文选取的数字资源服务绩效评价指标如表1所示。

表1 绩效评价指标Table 1 Performance evaluation index

3.2 样本数据选取

本文主要目标是为了验证所提出的评价模型和方法的可行性与准确性，为了便于说明，我们以山东省内高校、科研院所的数字图书馆提供的数字资源为例，采集其2005—2010年的统计数据为研究对象。对样本数据进行初步的分析，剔除难以获取的数据和上述指标数据不完整的数字资源样本，得到的研究样本共计120家，其中训练样本和检验样本数量分别为80和40。

3.3 实验及仿真训练

随着输入维数的增加，FNN的模糊规则数量将按照指数级增加，因此，当输入节点的数量过多时，就必然会增加模糊神经网络的结构复杂度，进而增加网络训练的时间。为有效地克服上述问题，同时在最大程度上减少主观因素对于网络评价结果的影响，本文所采用的神经网络将利用分层次的递接评价方法。该方法首先利用BP神经网络训练样本数据，对定性评价指标则采用模糊神经网络进行训练和学习，对经过BP网络和FNN网络训练得到的结果再利用FNN进行模糊评价，最终得到数字资源绩效评价的结果。我们假设最终的评价结果集合为F:Y→Z={优、良、中、差}。其中，Y为模糊神经网络的最后输出结果，Z为数字资源对应的绩效评价等级。

本文构建的BP神经网络为3层结构，其中输入层神经元数个是20，输出层神经元个数为1(输出结果为数字资源服务绩效的等级)。利用逐次对比和试用的方法，最终确定当隐含层神经元数为15时，BP神经网络的训练误差最小，训练时间最短。BP神经网络训练的误差曲线如图2所示。

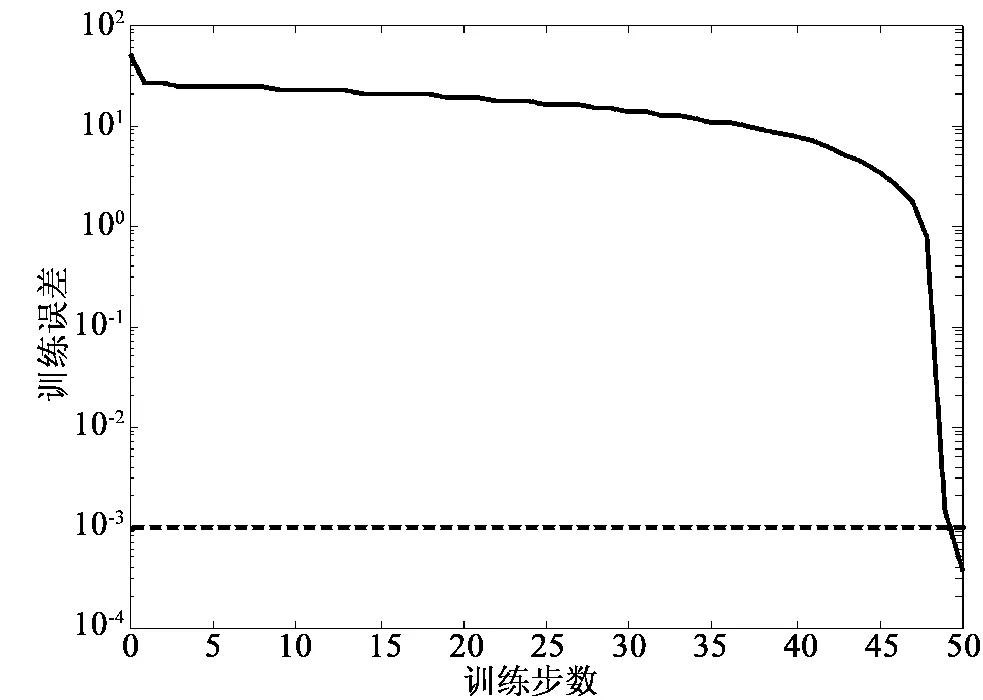
图2 BP神经网络训练误差曲线Fig.2 Training error curve of BP neural network

图3 FNN均方误差变化曲线Fig.3 Mean square error curve of FNN

图4 FNN的实际输出与期望输出Fig.4 Practical output and expected output of FNN

由定性评价指标构建的模糊神经网络FNN，由6个输入指标、1个模糊输出和由16个神经元组成的模糊化层组成，该网络的模糊规则数量为256(实验分析得出)。

最终构造的FNN包含2个输入节点(定量评价指标等级结果和定性评价指标等级结果)、1个输出节点(数字资源服务绩效评价结果)，其中的模糊化层包含12个神经元，模糊规则数为24条。网络训练过程中产生的均方误差曲线如图3所示。

从图3中可以得到，样本数据训练的均方误差曲线相对平稳，当均方误差达到1.7843×10－5时，神经网络的学习效果为最好。

最后把检验样本数据输入到训练完成的模糊神经网络中，进行数字资源服务绩效评价。我们得到网络的期望输出(用户主观评价结果)与网络实际输出如图4所示，其中平均误差为0.0019。

从图4我们可以得到，本研究提出的模糊神经网络评价模型能够较好地完成电子资源绩效评价的任务，绩效评价的时间效率和准确率都比较理想。通过对实验结果的分析，我们发现模糊神经网络电子资源绩效评价的准确率达到了83.7%，表明基于模糊神经网络的电子资源绩效评价模型和方法是切实可行的。

4 结语

本研究提出的模糊神经网络电子资源绩效评价模型方法，较好地完成了电子资源绩效评价的任务，并且由于有效地克服了传统的基于统计的评价模型与方法的不足，减少了主观因素对评价结果的影响，提高了评价结果的客观性和准确率。

［1］曾照云，张永杰，杨兰芝.数字资源服务绩效评估研究综述［J］.图书馆和信息服务，2008，52(8):54－57.

［2］余胜.关于图书馆绩效评估的研究与实践［J］.中国图书馆学报，2006(4):101104.

［3］索传军，王建朋.国外电子资源在线使用统计研究述评［J］.图书馆，2006(6):43－46.

［4］BLIXRUD J C.Measures for electronic use:The ARL E-metrics project［J］.Statistics in Practice-Measuring＆ Managing，2002，9:73－84.

［5］MILLER R，SCHMID S.E-metrics:Measures for electronic resources［J］.The Journal for the Serial Community，2002，15(1):19－25.

［6］索传军.论电子资源在线使用统计数据的收集与分析［J］.中国图书馆学报，2006，32(3):65－68.

［7］张秀华，杨洪勇，宋艳梅.基于灰色关联分析和BP神经网络的数字资源服务绩效评价研究［J］.情报学报，2010，29(3):468－473.

［8］黄颖.图书馆电子资源绩效评价模型构建分析［J］.现代情报，2009，29(8):106－107.

［9］史继红.两个重要的电子资源使用绩效评价体系的比较:欧洲的EQUINOX项目与美国的ARL E-metrics项目［J］.数字图书馆论坛，2007，38(7):53－57.

［10］ZHANG Y.Application of T-S fuzzy neural network based on declination compensation in soft sensing［J］.Mathematics and Computers in Simulation，2011，32(12):1 －8.

［11］BARBOUNIS T G，THEOCHARIS J B.A locally recurrent fuzzy neural network with application to the wind speed prediction using spatial correlation［J］.Neurocomputing，2007，70(10):1525 －1542.

［12］KHAYAT O，EBADZADEH M M，SHAHDOOSTI H R，et al.A novel hybrid algorithm for creating self-organizing fuzzy neural networks［J］.Neurocomputing，2009，73(1):517 －524.

［13］DENG X S，WANG X Z.Incremental learning of dynamic fuzzy neural networks for accurate system modeling［J］.Fuzzy Sets and Systems，2009，160(5):972 －987.

［14］LENG G，McCINNITY T M，G Prasad，et al.An approach for on-line extraction of fuzzy rules using a self-organizing fuzzy neural network［J］.Fuzzy Sets and Systems，2005，150(10):211 －243.

［15］YE B，YU Z，PAVLIKOVSKAYA E，et al.The neo-fuzzy neural network structure optimization using the GMDH for the solving forecasting and classification problems［C］//IWIM，2009.Krynica，Poland:IEEE computer society，2009:77 －89.

［16］LIN C T，YEH C M，CHUNG J F，et al.Suppoet-vector-based fuzzy neural networks［J］.International Journal of Computational Intelligence Research，2005，1(2):138－150.

［17］QIAO J F，WANG H D.A self-organizing fuzzy neural network and its applications to function approximation and forecast modeling［J］.Nurocomputing，2008，71(2):564－569.

［18］ALIEV R A，GUIRIMOV B G，FAZLOLLAHI B，et al.Evolutionary algorithm-based learning of fuzzy neural networks:Recurrent fuzzy neural networks［J］.Fuzzy Sets and Systems，2009，160(8):2553 －2566.

［19］NAIR T M，ZHENG C L，FINK J L，et al.Rival penalized competitive learning(RPCL):A topology-determining algorithm for analyzing gene expression data［J］.Compute Biol Chem，2003，27(6):565－574.