多层印制电路板边缘辐射的一种精确计算方法

胡玉生 温舒桦 范 峻

(1.集美大学机械与能源工程学院，福建 厦门 361021；2.北京邮电大学电子工程学院，北京 100876；3.EMC Laboratory，Missouri University of Science and Technology， Rolla， MO 65409， USA)

引 言

多层印制电路板(Printed Circuit Board,PCB)的电源分布网络，即电源/地(Power/Ground,P/G)平面形成了平行板谐振结构，当P/G平面的尺寸与波长相比拟时会从电源/地平面边缘产生显著的电磁波辐射干扰.

文献[1-3]等采用腔模理论研究了矩形PCB的辐射发射问题，文献[4-5]等采用时域有限差分(Finite-Difference Time-Domain,FDTD)全波分析方法对PCB的辐射发射进行了建模分析，FDTD法虽适宜解决复杂模型，但网格离散数量庞大，计算十分耗时，占用计算机资源较多.文献[6-9]采用边界积分方程法研究了电源/地平面上多过孔之间的耦合关系或电源/地平面的辐射发射.由于电源/地平面的辐射只需计算周围边界的场分量，基于边界离散的积分方程法或边界元法具有突出的优点，计算效率高，且可应用于任意形状的PCB.

目前关于电源/地平面辐射发射的研究大多是在过孔处施加假设的电流作为激励源，未能准确评估PCB实际的辐射场.本文的贡献在于通过场路结合的计算方法获得了精确的辐射发射激励电流，从而可精确预测PCB的辐射值.

1 电源/地平面场分布的边界元算法

多层印制电路板的一对P/G平面结构如图1所示.电源层和地层均为厚度很小的导体，间距为h，填充介质的相对介电常数为εr，损耗正切为tanδ.P/G平面上通常含有若干过孔，为简化起见，本文中的模型仅包含一个信号过孔.辐射发射由P/G平面四周的边缘场产生，信号过孔耦合到P/G平面的电流为辐射发射的激励电流.

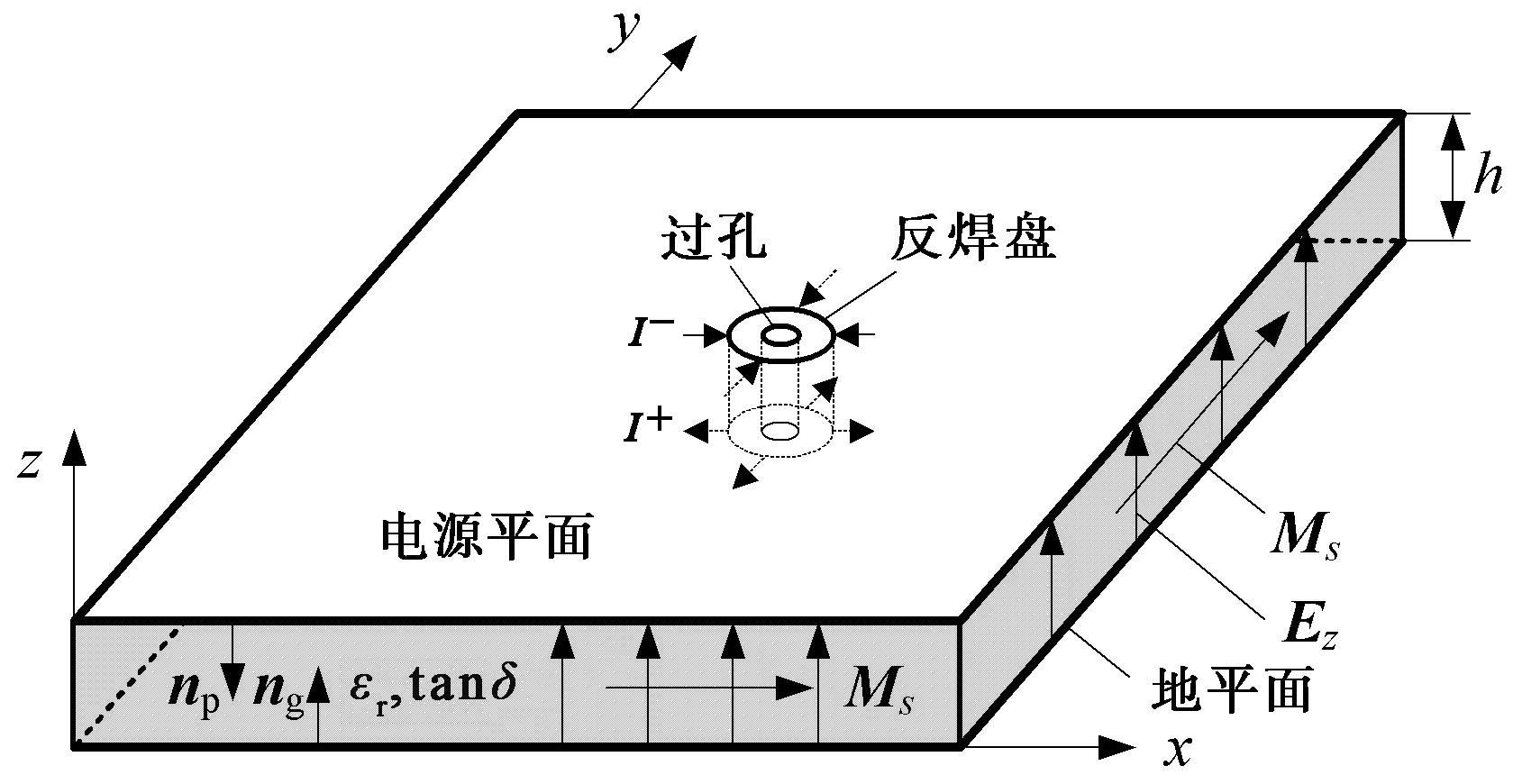
图1 电源/地平面的结构

P/G平面的间距h与波长相比很小，可以认为电磁场沿厚度方向没有变化，Hz=Ex=Ey=0，场分布只有沿z方向的电场分量Ez以及xy平面上的磁场分量Hx和Hy，移去过孔后图1中的三维结构可简化为一个二维问题.边界元法的计算模型及边界离散见图2.P/G平面间的场分布控制微分方程为亥姆霍兹方程，即

(1)

式中：u=Ez；k为传播常数，考虑介质损耗，

(2)

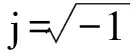
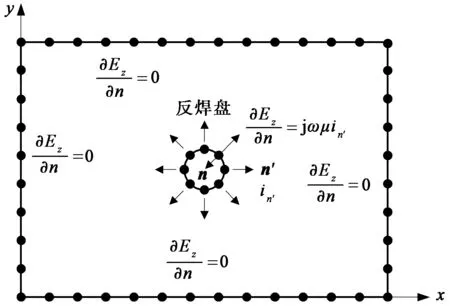
图2 边界元计算模型及边界离散图

设在地平面上电流I+从反焊盘边缘向四周扩散，在电源平面上对应的返回电流I-从四周向反焊盘边缘汇聚.设地平面上表面的电流密度为i(ix，iy)，单位法向量为ng(见图1)，根据i=ng×H可求出磁场与电流密度的关系为：

Hy=-ix；Hx=iy.

(3)

设电源平面下表面的单位法向量为np，对电源平面也可得到与式(3)相同的结果.P/G平面的介质内无电流，但反焊盘处的磁场可等效为激励电流，激励电流与磁场的关系满足关系式(3).

由麦克斯韦第一方程

(4)

得:

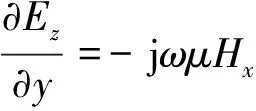
(5)

(6)

式中：μ为磁导率；ω为角频率.令图2中反焊盘边界外法线方向为n，由于

(7)

(8)

将式(3)、(5)、(6)代入式(7)、(8)，得

(9)

式中：ax、ay分别为x、y方向的单位向量；in为反焊盘处沿外法向量n的电流密度in′，而给定的实际电流密度为沿反焊盘内法向量的in′=-in，因而反焊盘处的边界条件为

(10)

在电源/地平面的外周边界，因无电流流出，in=0，为磁壁边界条件为

(11)

控制方程(1)及边界条件(9)、(10)构成了模型的边值问题.根据边界元法可推导出边界上任一点i的电场ui可表示为边界上的积分方程

(12)

式中：S为积分边界；q=∂u/∂n；ci=1-θ/(2π)，θ是i点处的平面角；u*为自由空间的格林函数，u*、q*分别给定如下[10]：

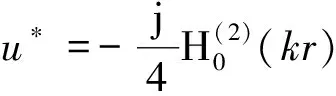
(13)

(14)

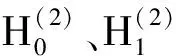
采用线性元法将场域边界离散为N个元素，式(12)写成离散形式为

(15)

对N个单元最终可形成N个方程组，代入边界条件可求得边界上各节点的Ez值.电源/地平面四周表面的等效磁流密度Ms与电场Ez的关系为

Ms=-ns×Ez.

(16)

式中，ns为电源/地平面四周表面的单位法向量.

2 辐射场的计算

忽略P/G平面厚度的影响，Ms产生的电矢位F为

(17)

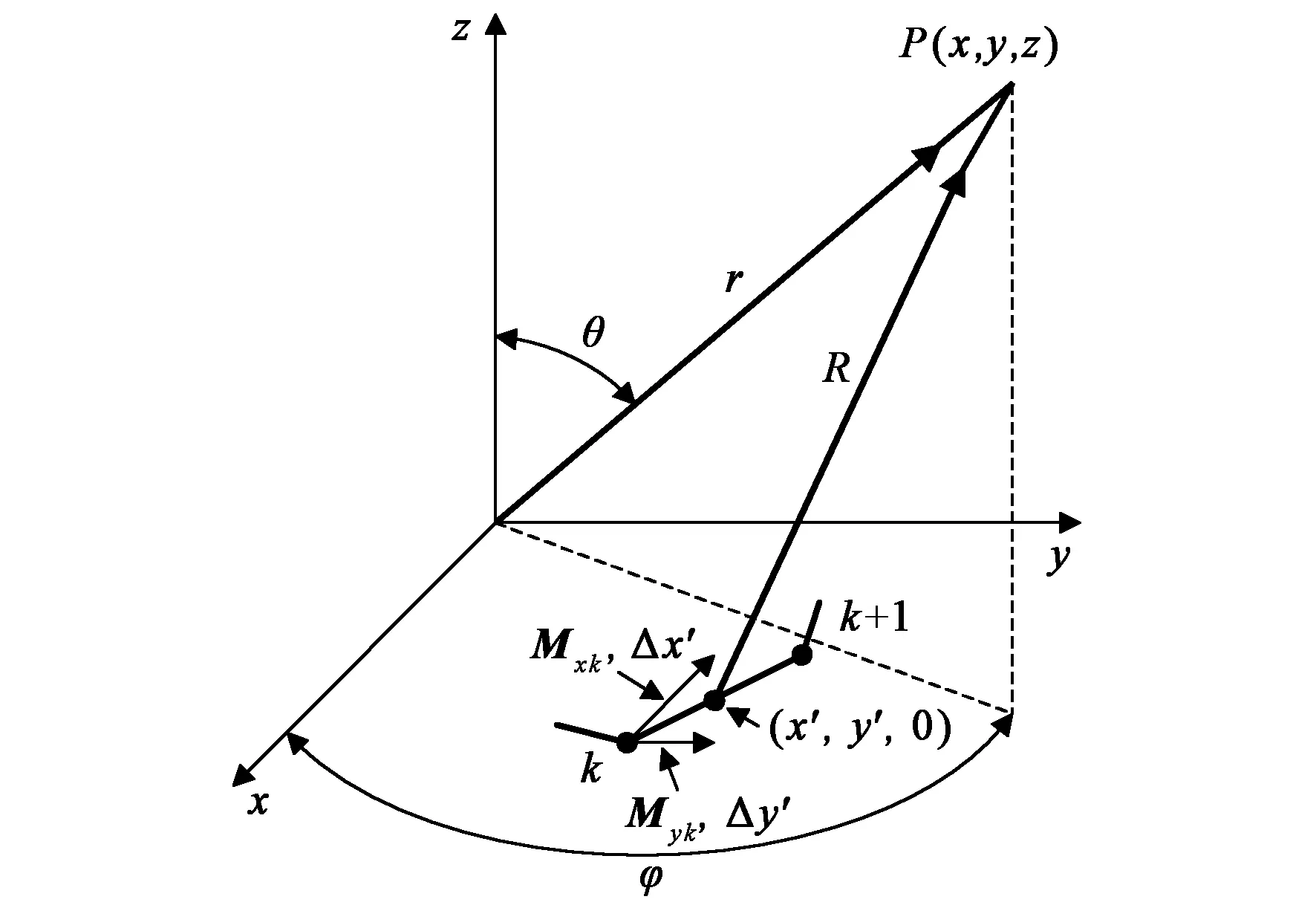
图3 等效磁流辐射发射的几何关系

式中：R是P/G平面周围边界上的任一点到观察点的距离；C是整个周边积分边界； dl′是积分微元.等效磁流辐射发射的几何关系见图3.设任一单元k内的磁流密度Msk为定值，Msk取为其节点k和k+1的磁流密度的平均值.当单元尺寸很小时，可忽略单元内各点到空间观察点P(x，y，z)产生的相位差，因而单元k内任一点到点P的距离可近似为单元中心点(x′，y′，0)到P点的距离，即

(18)

在直角坐标系中，将Msk分解为x、y分量Mxk和Myk，对应的电矢位分别为Fxk和Fyk，单元长度在x、y方向的投影分别令为Δx′、Δy′.

式(17)电矢位的离散形式可写为

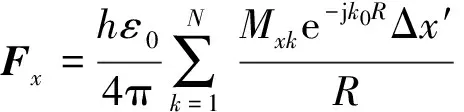
(19)

(20)

由以下公式将电矢位由直角坐标变换为球坐标:

Fθ=Fxcosθcosφ+Fycosθsinφ;

(21)

Fφ=-Fxsinφ+Fycosφ.

(22)

辐射电场为电矢位F的旋度，即

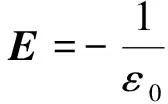
(23)

由于远区场可视为沿r向传播的横电磁波，可由平面波场的简化算法直接得出[11]

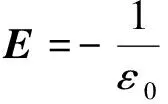
(24)

式中，ar、aθ、aφ是球坐标系中的单位矢量.因而

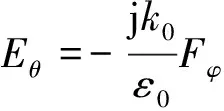
(25)

(26)

总电场强度辐值|E|为

(27)

3 辐射发射激励电流的计算方法

以图4为例，对一个简单四层电路板结构进行阐述，电路板上有一个信号过孔，并与一个简单的外部电路相连.四层板的顶层和底层为信号层，第二层为电源层，第三层为地层.信号电流从顶层通过过孔传送到底层.顶层和底层信号电流的返回路径分别为第二层上表面和第三层下表面；过孔电流的返回路径为P/G平面[12].

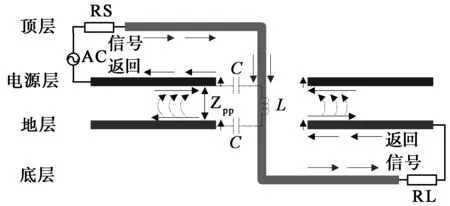
图4 一个四层电路板结构及返回电流路径

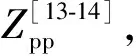
(28)

式中，Ia为反焊盘处施加的已知电流.

忽略损耗，过孔段可采用一节LC等效π模型集总电路表示，其与外部电路连接形成完整的整体电路.图4所示电路结构的等效SPICE模拟程序电路模型见图5.经电路仿真可求得流经Zpp的电流，亦即辐射发射的激励电流Ihole，然后以激励电流Ihole为反焊盘处的边界条件通过边界元法求得P/G平面边缘的场分布，进而求得远区辐射场.

图5 过孔转换结构的等效电路模型及整体电路

4 计算结果

图4所示电路实例的结构尺寸见图6，PCB长40 mm，宽20 mm；位于顶层和底层的走线长度均为15 mm；信号源内阻及负载阻抗均为50 Ω，走线的特性阻抗亦令为50 Ω；信号过孔位于PCB板的中心，过孔直径为20 mil(1 mil=0.025 4 mm)，反焊盘直径为80 mil；电源层和地层的间距h=1.4 mm，走线距离电源层和地层均为0.5 mm，走线宽10 mil；PCB板间介质材料为FR4，相对介电常数为εr=4.5，损耗正切tanδ=0.02.

顶层和底层走线呈微带线结构，分别用一节Γ型集总电路表示.根据Zpp呈容性或感性，Zpp用电容Cpp或电感Lpp代替，Cpp=1/(ωZpp)，Lpp=Zpp/ω.则图6的PCB电路转化为图7的电路模型.

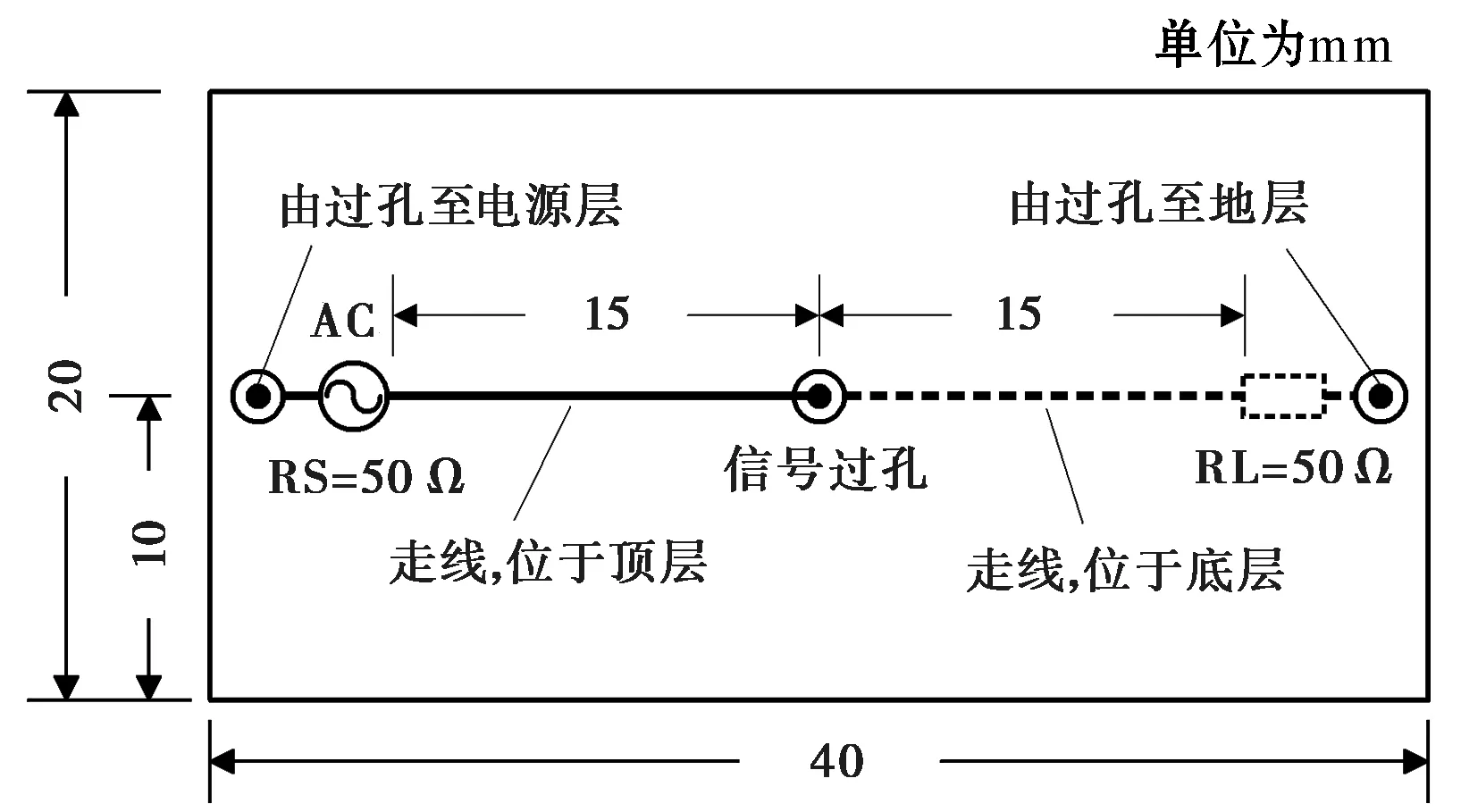
(a) 俯视图

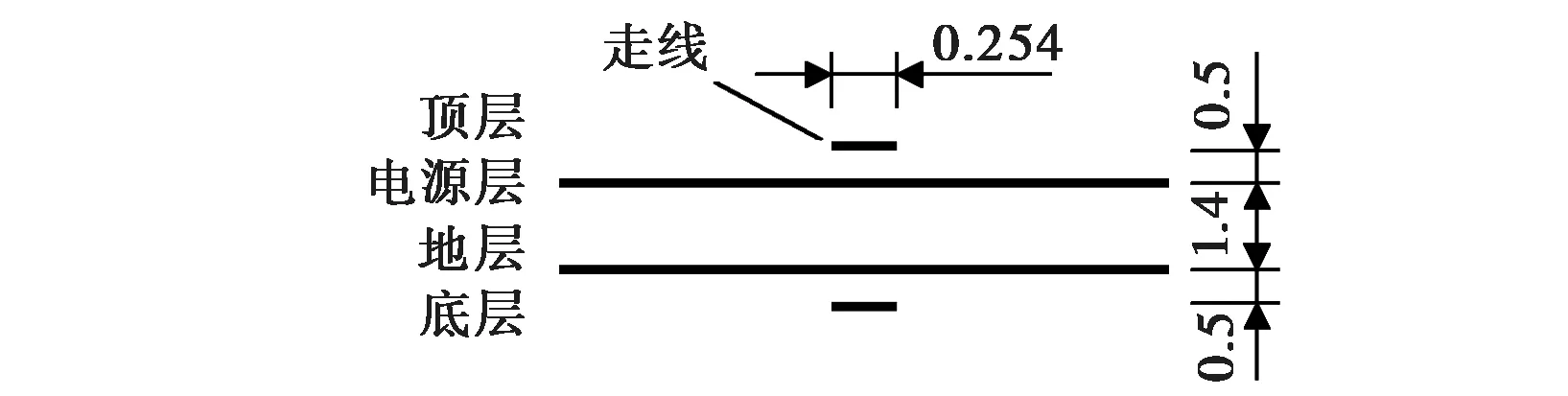
(b) 俯视图图6 计算实例的结构尺寸(单位：mm)

图7 计算实例的SPICE整体电路模型

过孔与P/G平面的电容采用采用轴对称有限元法计算[15]，得过孔的总电容Ctotal=0.213 pF，将该总电容分配给过孔π模型电路的电容C2、C3，C2=C3=Ctotal/2=0.106 5 pF.设过孔单位长度的电容和电感分别为c和l，则c=Ctotal/h=0.152 nF/m，由

(29)

得l=32.9 μH，其中v为相速度，v0=3×108m/s.从而可得过孔π模型中的电感L2=lh=4.144 7 nH.

计算得走线单位长度的电容、电感分别为：c=94.1 pF/m、l=0.532 μH，则走线的总电容为C1=C4=94.1×0.015 pF=1.41 pF，走线的总电感为L1=L3=0.532×0.015 μH=7.98 nH.

计算频率从10 MHz到5 GHz，步长为10 MHz，采用边界元法计算得反焊盘处的Zpp曲线见图8.在图8中相位为-90°的频率处Zpp呈容抗，相位为+90°的频率处Zpp呈感抗.在1.33 GHz、4.16GHz处为谐振频率点，Zpp有极小值；在3.55 GHz处为反谐振频率点，Zpp有极大值.

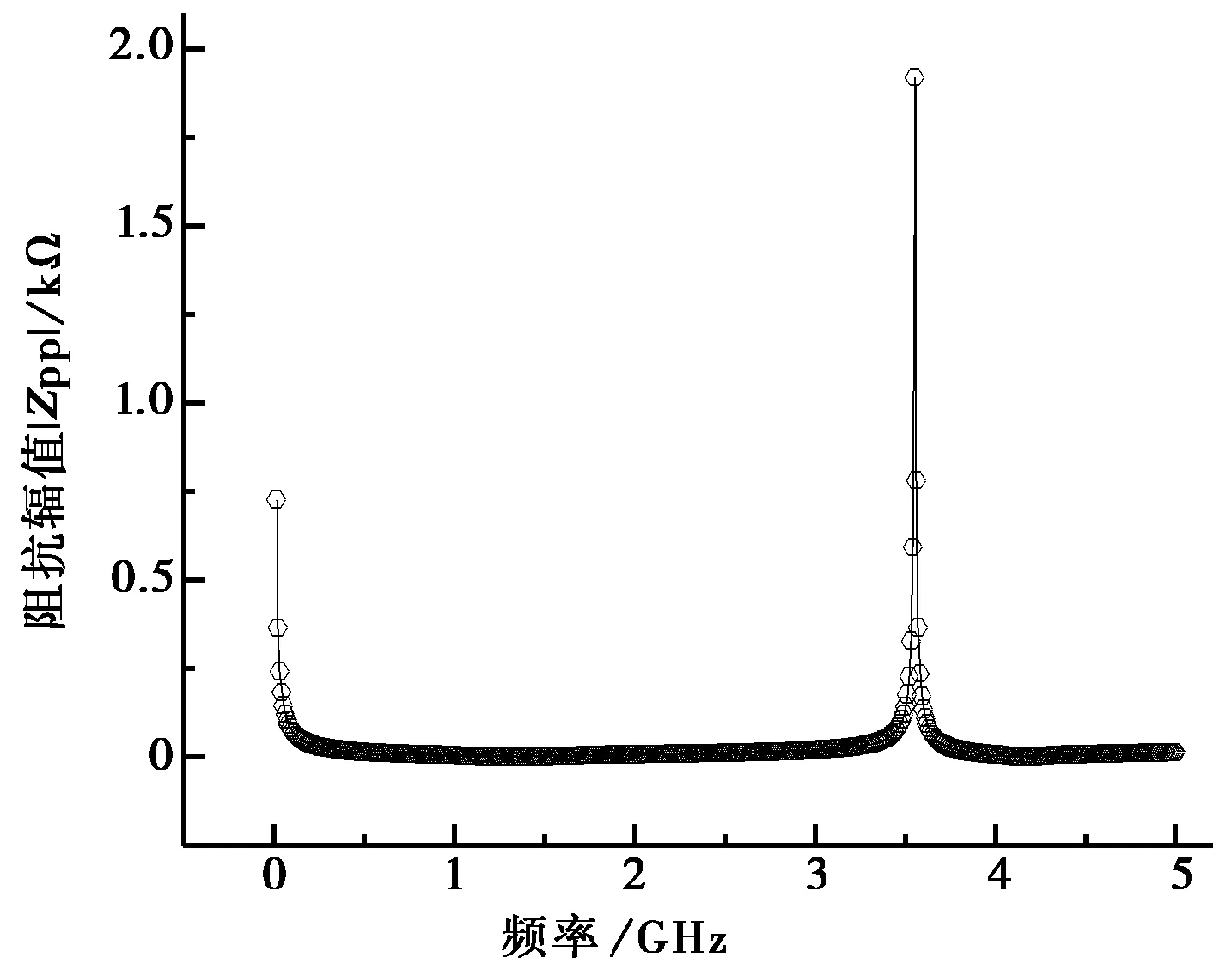
(a) Zpp的辐值

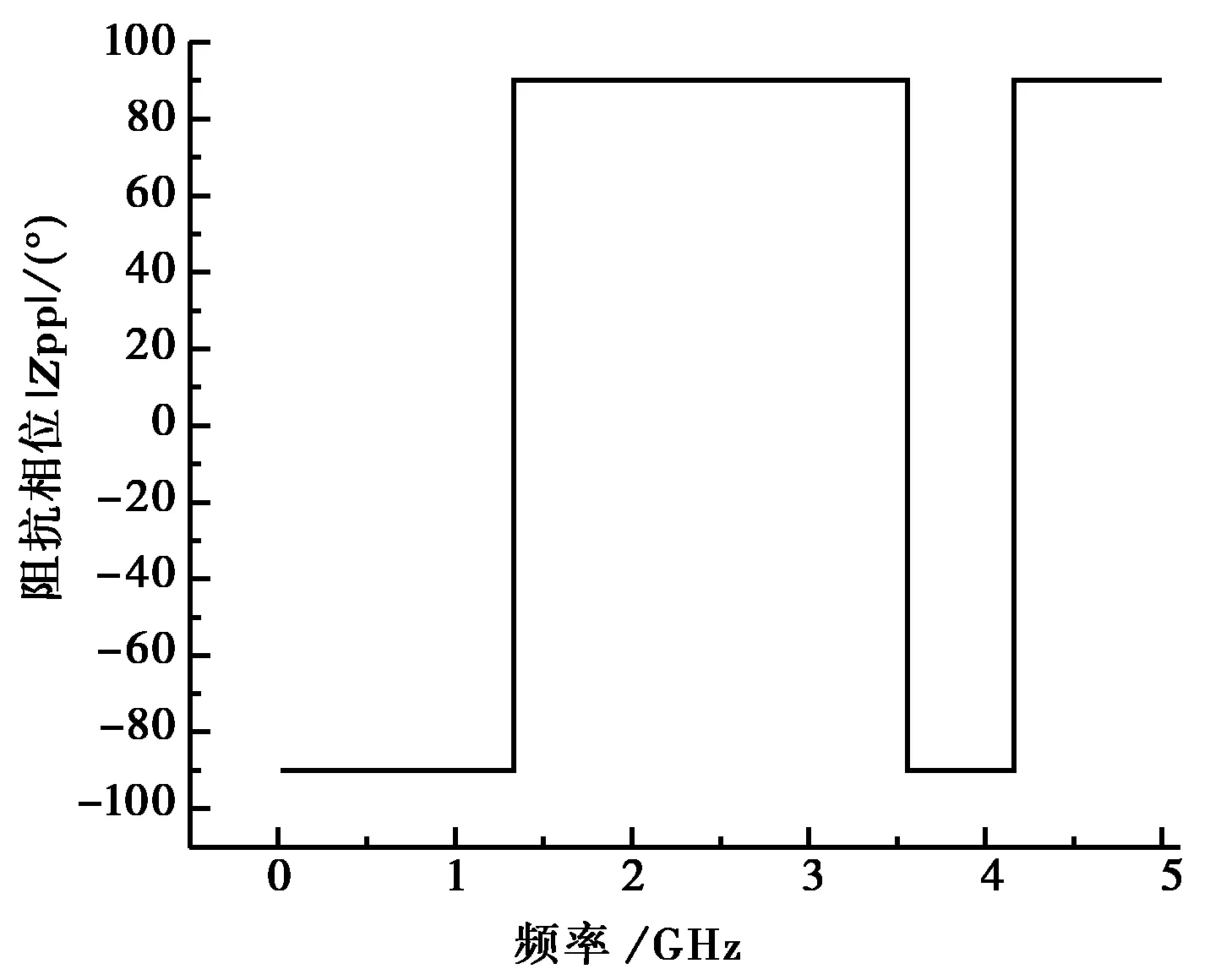
(b) Zpp的相位图8 不同频率时的Zpp

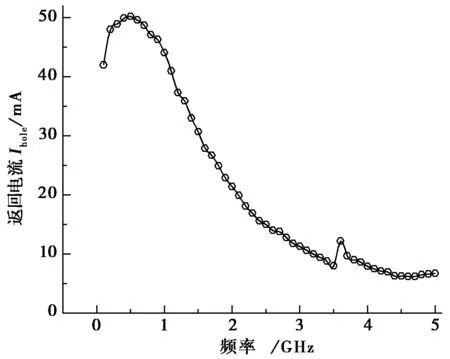
图9 电源/地平面反焊盘处的返回电流

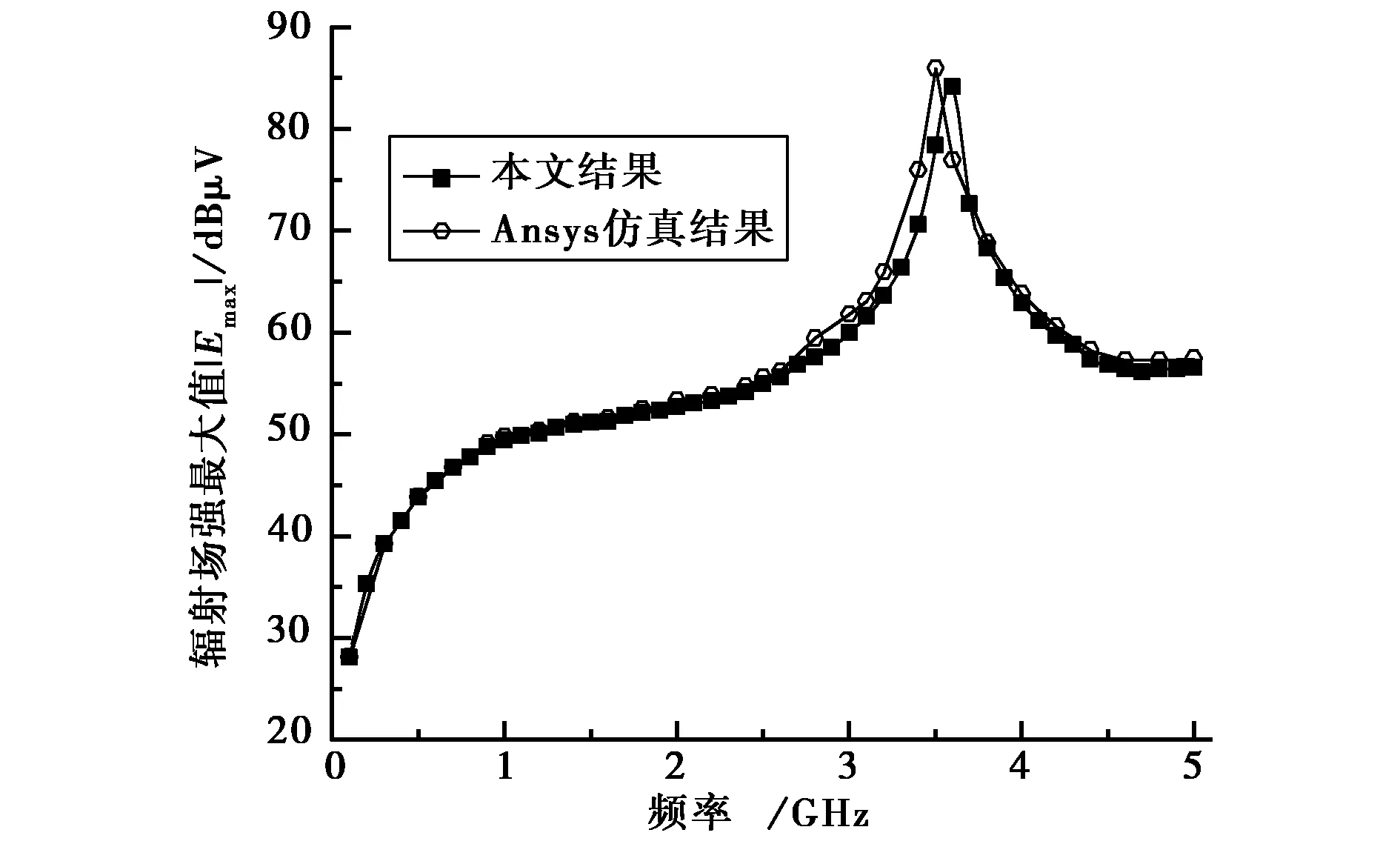
图10 距PCB板10 m处不同频率的最大辐射场强

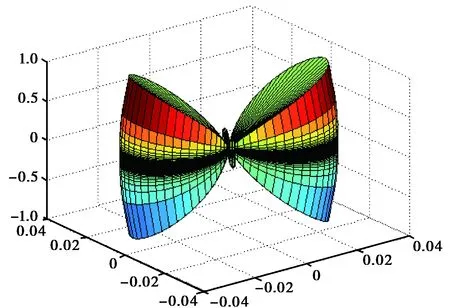
(a) 1 GHz

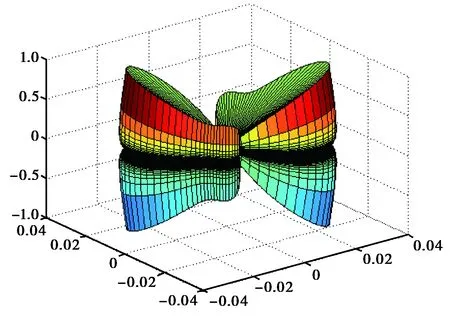
(b) 3.55 GHz图11 电源/地平面的辐射方向图

由Zpp及图7电路可计算出不同频率时流经P/G平面反焊盘处的返回电流Ihole.设交流信号源的辐值为5 V，计算结果见图9，由图9可知，在500 MHz附近Ihole最大，随频率提高返回电流逐渐下降，当频率为3～5 GHz，Ihole将保持在一个相对稳定值.

由激励电流Ihole计算得离PCB板10 m处不同频率时的最大辐射场强见图10.由图10可以看出，在频率较低的频段尽管激励电流较大，但辐射值相对较小，随频率提高辐射值逐渐增加;在3.55 GHz的反谐振点处突变到极大值.1 GHz和3.55 GHz的辐射方向图见图11.采用Ansys电磁场有限元全波分析软件进行验证，结果基本吻合.

5 结 论

将过孔转换结构的等效物理电路模型与外部电路组成整体电路，通过电路仿真可获得多层印制电路板电源/地平面精确的辐射发射激励电流.采用边界元法对电源/地平面的边缘场分布及反焊盘处返回电流的阻抗进行分析，可显著减少单元离散数量，计算效率和计算精度高，特别适宜处理精细的过孔等结构.计算结果表明，在反谐振频率处辐射场有极大值，其原因是在反谐振频率处信号返回路径阻抗最大，电流返回路径受到阻断，因而辐射场大幅增加.采用全波分析的电磁场有限元软件对本文计算结果进行了验证.场路结合的方法便于与现有电路设计分析软件集成，是分析多层PCB辐射发射的一种有效方法.

[1] LEI G-T，R TECHENTIN R W，GILBERT B K.High-frequency characterization of power/ground-plane structures[J].IEEE Trans Microw Theory Tech，1999，47(5):562-569．

[2] LEONE M.The radiation of a rectangular power-bus structure at multiple cavity-mode resonances[J].IEEE Trans Electromag Compat，2003，45(3):486-492．

[3] SHIM Hwan-Woo，HUBING T H.A closed-form expression for estimating radiated emissions from the power planes in a populated printed circuit board[J].IEEE Trans Electromag Compat，2006，48(1):74-81．

[4] FORNBERG Per E，BYERS Andrew，PIKET-MAY Melinda.FDTD modeling of printed circuit board signal integrity and radiation[C]//IEEE Inter Symp Electro-mag Compat，Washington DC，Aug 2000，1:307-312．

[5] YE Xiaoning，HOCKANSON M David，LI Min，et al.EMI mitigation with multilayer power-bus stacks and via stitching of reference planes[J].IEEE Trans Electromagn Compat，2001，43(4):538-548．

[6] WEI X,LI E，LIU E,et al.Efficient simulation of power distribution network by using integral-equation and model decoupling technology[J].IEEE Trans Microw Theory Tech，2008，56(10):2277-2285．

[7] STUMPF M，LEONE M.Efficient 2-D integral equation approach for the analysis of power bus structures with arbitrary shape[J].IEEE Trans Electro-mag Compat，2009，51(1):38-45．

[8] ZHANG Yaojiang，FAN Jun.An intrinsic circuit model for multiple vias in an irregular plate pair through rigorous electromagnetic analysis[J].IEEE Trans Microw Theory Tech，2010，58(8):2251-2265．

[9] ZOU G，LI E，WEI X，et al.EMI and EMC analysis of arbitrarily shaped power-ground planes[C]//Asia-Pacific Inter Symp Electromag Compat，Beijing，April， 2010:12-16．

[10] 曹世昌.电磁场的数值计算和微波的计算机辅助设计[M].北京:电子工业出版社，1989．

CAO S.Numerical calculation of electromagnetic and computer aided design for microwave[M].Beijing:Electronic Industry Press，1989.(in Chinese)

[11] EDWARDS T C.Fundation for microstrip circuit design.New York:John Wiley &Sons，1981．

[12] BOGATIN E.Signal integrity:simplified[M].New Jersey:Prentice Hall，2004．

[13] WEI X，LI E，LIU E，et al.Efficient modeling of re-routed return currents in multilayered power-ground planes by using integral equation[J].IEEE Trans Electromagn Compat，2008，50(3):740-743．

[14] ZHANG Yaojiang，FENG Gang，FAN Jun.A novel impedance definition of a parallel plate pair for an intrinsic via circuit model[J].IEEE Trans Microw Theory Tech，2010，58(12):3780-3789．

[15] 杨荣彬，胡玉生.采用轴对称二维有限元法提取过孔分布电容[J].安全与电磁兼容，(2)，2012:69-72．

YANG Rongbing，HU Yusheng.Extracting via capacit-ance of PCB using axially symmetric two-dimensional FEM Method[J].Safety & EMC，2012(2)：69-72.(in Chinese)