基于高斯和粒子滤波的动态称重数据处理
2013-04-13张丽妹高占宝尹志兵
张丽妹,高占宝,尹志兵
(1.北京航空航天大学自动化科学与电气工程学院,北京100191;2.中山市精威包装机械有限公司,广东中山528425)
0 引言
近年来国内外称重技术研究取得了显著进展,主要表现在称重测量技术由静态测量向动态测量、在线测量和模型化方向发展[1]。所谓动态称重即称重信号处于动态变化之中,没有达到稳态,在动态测量中较快地准确地获得称重值是目前动态称重时急需解决的问题。然而由于动态称重过程中机械振动等影响,导致测量数据存在很大的噪声,为了得到准确的称重值需要对测量信号进行滤波处理。
目前常用于处理称重数据的滤波方法有中值滤波法、滑动平均滤波法等传统滤波方法,但是这类传统的滤波方法难以克服测量数据的非线性,对于处理强非平稳数据难以得到较好的结果。为此本文在利用已有测量数据对系统建立模型的基础上,采用基于模型的滤波方法对测量数据进行处理。在此类基于模型的滤波方法中卡尔曼滤波堪称经典,卡尔曼滤波是噪声服从高斯分布的线性系统最优滤波,对非高斯非线性系统,卡尔曼滤波不能达到最优估计效果。粒子滤波是一种基于递推贝叶斯估计的蒙特卡洛实现方法,在处理非线性非高斯系统问题上有着明显优势[2]。
对于卡尔曼滤波及扩展卡尔曼滤波,需假设分布为高斯分布,若真实分布为非高斯分布,则单一高斯分布难以很好地描述,可考虑用高斯和分布来近似真实分布。为此本文提出了基于高斯和粒子滤波的处理方法,并对称重系统进行建模。,仿真结果证明采用高斯和滤波进行处理的方法在提高称重的快速性与精确性上有很好的效果。
1 粒子滤波原理
粒子滤波是递推贝叶斯估计的一种蒙特卡洛实现方法,让样本粒子通过系统模型按时间顺序向前传播,得到各时刻系统的状态样本,从而求得系统状态的后验概率密度函数。序贯蒙特卡洛方法的核心思想是用一组带权随机样本集代表后验分布函数,并基于这些样本计算概率值。
离散的动态状态空间模型可描述为
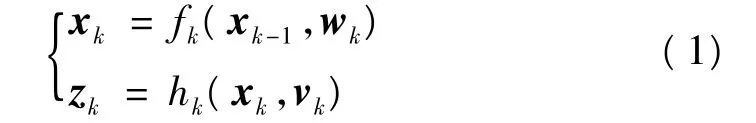
式中:xk∈Rn为k时刻状态变量;zk∈Rm为k时刻得到的测量向量;wk,vk为过程噪声与观测噪声;fk为量测函数;hk为观测函数。
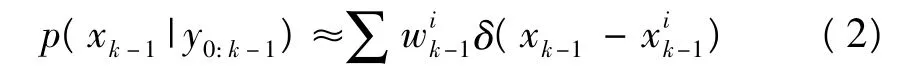
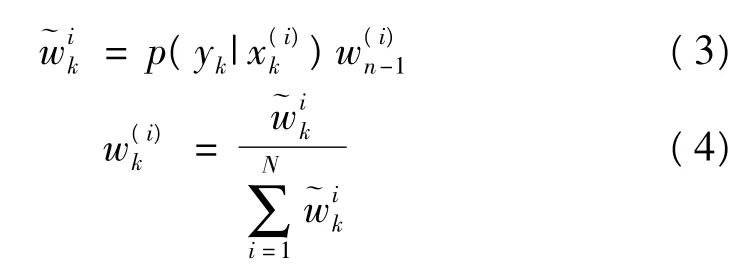
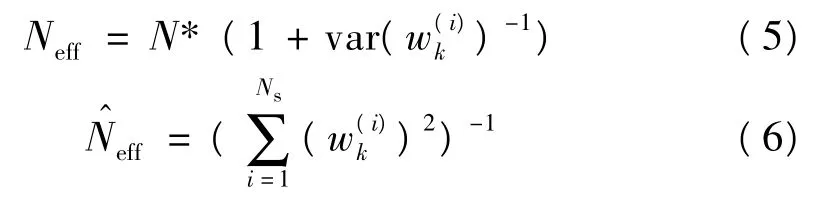

重抽样过程虽然在一定程度上解决了粒子退化问题,但是重抽样会带来新的问题。例如,重抽样总是倾向于复制最合适的粒子,并将导致不合适的粒子子代为零。在极端情况下,这又将导致一种粒子退化,损失了粒子的多样性。
2 高斯和粒子滤波
为了避免上述粒子贫化问题,提出了高斯和粒子滤波方法,该方法结合高斯混合逼近后验分布的思想,并采用蒙特卡洛采样和更新策略。
2.1 高斯混合逼近
可证明任何概率分布p(x)可由如下密度pG(x)无限逼近:

式中:G为混合部分的个数;Φ={α1,…,αG,φ1,…,φG}为高斯混合模型的参数,且φi={μi,∑i};αi为混合权重;N(x;μi,∑i)表示均值为μi方差为∑i的正态分布。逼近误差可为任意小[4]。
2.2 高斯和粒子滤波
在高斯和粒子滤波中,采用高斯混合模型来逼近后验分布。
在时间更新阶段,假设时间的后验分布为p(xk|y0:k)并且可用高斯和来表达[5],即

则预估分布为

积分可由高斯混合模型逼近为

在测量更新过程,当新的测量值yk+1到达时,可通过贝叶斯估计算法更新后验密度[6]:
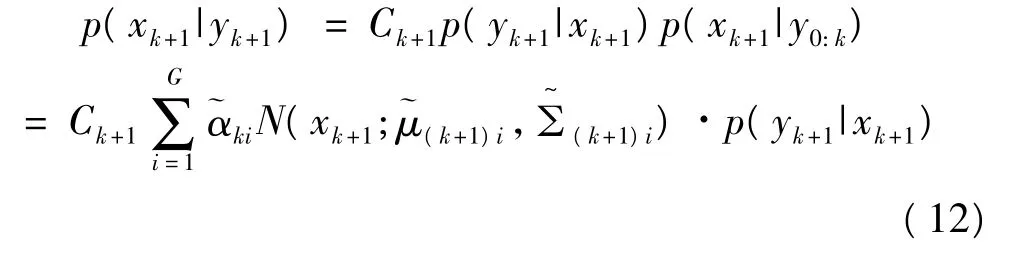
1)对i=1,…,G,从重要性分布中采样M个样本,记作。
2)i=1,…,G;j=1,…,M。计算相应权重为

式中:π(xk|y0:k)为建议分布。当假设先验分布为重要性分布时,权重计算如下:
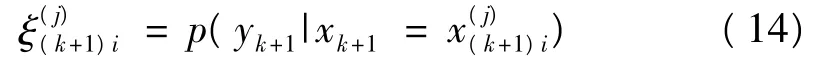
3)由于
4)更新高斯混合分布的权重为

5)归一化权重

在此基础上可得后验分布为

则状态xk+1的估计可计算如下
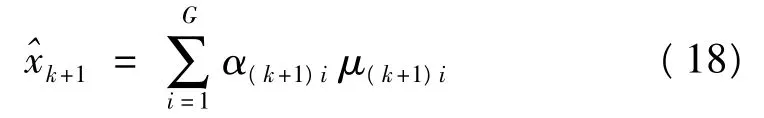
这种方式避免了粒子滤波的重采样步骤,从而避免了粒子滤波的退化问题,而且高斯和粒子滤波以高斯和分布逼近非高斯噪声,较粒子滤波更精确。下面通过具体实例数据来验证这一点。
3 实例验证
为验证高斯和粒子滤波在动态称重数据处理方面的效果,本文采集了大量动态组合秤实测数据,并分别用EKF(扩展卡尔曼滤波)、PF(粒子滤波)、GSPF(高斯和粒子滤波)对数据进行处理,将处理结果进行对比研究。现以一组60 Hz 采样频率、标称称重500 g的采集数据为例,说明本文方法的优点。
3.1 称重系统建模
上述滤波方法需要对系统进行建模。传统的分析系统物理结构进行建模的方法,过程复杂且需要一定的专业知识,而系统的输入输出数据从一定程度上反映了系统的结构,为此本文采用基于数据的建模方法[8]。由于真实称重过程中会有物料下落的冲击力带来的强扰动,所以采用负阶跃测得数据对系统进行建模,即在称量盘上悬挂一定质量重物,在某时刻剪断绳子测量系统输出,这样就可以得到系统的负阶跃响应动态校准数据,进而可得到相对精确的模型。
对于上述算法应建立状态空间模型,采用损失函数及最终预报误差来衡量模型的精度,以选择模型的阶次。本文比较了二阶、三阶模型,各自的损失函数及最终预报误差值如表1所示。由表1 可以看出三阶模型较二阶模型精度提高很多,且两个指标数值已经很小,即模型较精确,考虑到计算复杂度问题无需采用更高阶模型。

表1 损失函数与最终预报误差比较
用此方法建立的状态空间模型如下:

其中,

Xk,Xk-1∈R3分别为k,k-1 时刻状态变量,Yk∈R 为k时刻观测向量,Uk∈R 为k时刻输入向量,ek-1,ek∈R 为过程噪声及观测噪声,均服从伽马分布。
3.2 仿真结果
为比较滤波效果,本文采用三种方式来衡量滤波效果:图形法直观定性比较、均方根误差定量比较、尺度函数定量比较。
图形法可以直观地看到各方法的处理效果,图形结果如图1、图2所示。图1 为三种滤波算法的结果图,可以看到PF 和GSPF 与真实状态很接近;图2 为图1 的局部细节图。由图2 可以直观看出PF 与GSPF较之EKF 方法降噪效果要好很多,EKF 的处理效果最差,GSPF 的处理效果最好。

图1 三种滤波算法结果

图2 滤波结果细节
为了定量衡量各方法的优劣,采用均方根误差表示真实状态与状态估计的差值[9]:

式中:n为观测点数;括号内为在t观测点处的绝对误差。三种方法的均方根误差比较见表1。由表1 可以看出,EKF 的均方根误差较其他两个大很多,这是由于初始部分大噪声导致的,这一点在图1 中可以清楚地看到,而PF 与GSPF 两方法的误差结果都较小,GSPF的均方根误差最小,估计状态与真实状态最接近,效果最好,这与图1、图2 得出的结果一致,从数量上更清楚地看到各方法效果的差距。

表2 均方根误差比较结果
上面两种方法是从滤波效果角度在定性与定量上比较了三种方法的优劣,得出了GSPF 方法最优的结论。然而从实际工程角度,滤波目的是要快速地得到精度较高的称重数据,即提高动态称重的速度与精度,为此需要得到能表征速度与精度的量。尺度函数是为衡量动态称重效果而编写的函数,用来在数量上衡量称重的速度与精度,分别用稳定时间与稳定误差来表示。稳定时间为从开始测量到数据进入稳定域的时间,稳定误差为稳定域内数据的分散程度,稳定时间越小表示称重速度越快,稳定误差越小表示称重精度越高。三种方法的对比结果如表2。由表2 可以看出EKF 的速度慢、精度差,而PF 的速度太慢,只有GSPF 的速度快且精度高,对动态称重数据处理有绝对的优势。

表3 称重效果对比
4 总结
为了提高动态称重的快速性与准确性,提高生产效率,针对动态称重过程的强非平稳性及过程噪声的复杂性,在对系统建模的基础上,本文提出了高斯和粒子滤波方法对动态称重数据进行滤波处理。仿真结果证明高斯和粒子滤波方法可以很好地滤除测量噪声,从而快速的得到较精确的测量值,并且与EKF 及PF方法作对比证明处理结果优于以上两种方法。
由于PF 及GSPF 方法是基于蒙特卡洛的统计分析计算方法,在计算量上要比EKF 大得多,但是由于现在计算机处理速度的提高,计算复杂度已不再是阻碍粒子滤波发展的障碍,因此粒子滤波系列算法近年来被广泛应用于处理非线性非高斯滤波问题。在此,通过仿真证明了该算法在动态称重数据处理方面的优势,要将此方法应用于生产过程中还需要做一些工作,可用并行方式利用FPGA(现场可编程门阵列)来在线实现该算法。
[1]Nledzwlecki M,Wasilewski A.Application of adaptive filtering to dynamic weighing of vehicles[J].Control Eng.Practice,1996,5(4):635-644.
[2]朱林富,张三同.基于粒子滤波的故障诊断方法研究[D].北京:北京交通大学,2010.
[3]Liu Qinming,Dong Ming,Peng Ying.A novel method for online health prognosis of equipment based on hidden semi- Markov model using sequential Monte Carlo methods[J].Mechanical Systems and Signal Processing,2012,5.
[4]Shaodong YANG,Desheng WEN,Jing SUN,Junyong MA.Gaussian Sum Particle Filter for Spacecraft Attitude Estimation[C]//2010 the 2nd International Conference on Signal Processing Systems.Dalian:IEEE,2010,3:566-570.
[5]Kotecha J H,Djuric P M.Gaussian Sum Particle Filering[J].IEEE Transactions on Signal Processing,2003,51(10):2602-2612.
[6]Oshman Y,Carmi A.Attitude Estimation from Vector Observation Using a Genetic-Algorithm-Embedded Quaternion Particle Filter[J].Journal of Guidance,Control and Dynamics,2006.7(29):879-891.
[7]Kotecha J H,Djuric P M.Gaussian sum particle filtering for dynamic state space models[C].//Proceedings of ICASSP-2001.Salt Lake City:IEEE,2001,5:3465-3468.
[8]Chaochao Chen,George Vachtsevanos,Marcos E.Orchard.Machine remaining useful life prediction:An integrated adaptive neuro-fuzzy and high-order particle filtering approach[J].Mechanical Systems and Signal Processing,2012,28:597-607.
[9]Wahyu Caesarendra,Gang Niu,Bo-Suk Yang.Machine condition prognosis based on sequential Monte Carlo method[J].Expert Systems with Applications,2010,37:2412-2420.
