基于蒙特卡洛法的常用玻璃量器容量测量结果不确定度评定

赵琳，李锁印，许晓青，韩志国，冯亚南

(中国电子科技集团公司第十三研究所，河北 石家庄050051)

0 引言

常用玻璃量器(以下简称量器)广泛应用在石油化工、食品卫生、环境检测等实验分析工作中。它包括滴定管、分度吸量管、单标线吸量管、单标线容量瓶、量筒和量杯六类玻璃量器，作为化学分析中最基础的计量器具，其准确度直接影响后续的分析结果。为了确保其计量数据的准确，量器的检定是非常重要和必要的。

量器的检定依据JJG196 －2006 《常用玻璃量器检定规程》进行，规程中对常用玻璃量器的容量允差进行了详细的规定，但仍不能满足一些行业部门对量器不确定度的要求。本文选用单标线容量瓶，对其进行不确定度分析，以满足各行各业应用玻璃量器的实验室的需要。容量测量结果不确定度的评定是我们建立“常用玻璃量器检定装置”和开展检定工作重要的依据。

1 测量不确定度分析

测量不确定度是与测量结果相联系的、表征合理地赋予被测量分散性的参数。从词意上理解，测量不确定度意味着对测量结果可信性、有效性的怀疑程度或不肯定程度，是定量说明测量结果的质量的一个参数。测量不确定度的评定方法有很多种，通常情况下是依据GUM 法对不确定度进行评定，但是当遇到以下情况时依据GUM 法进行评定得到的结果可能变得不可靠，如:①不宜对测量模型进行线性化等近似的场合;②输出量的概率密度函数(PDF)较大程度地偏离正态分布或t 分布，例如分布明显不对称的场合。蒙特卡洛法(MCM)比较适合这些情况下对不确定度的评定。MCM 法的主要特点为:

1)对于复杂或非线性模型，尤其是无需使用一阶或高阶偏导来提供不确定度传播律的灵敏系数，可减小分析难度。

2)非线性模型时，一般可改善输出量的估计。

3)非线性模型时，尤其是当各个输入量服从非正态(如不对称)概率密度函数(PDF)时，无需提供高阶导数即可改善输出量的估计的标准不确定度。

4)当输出量的PDF 不能由正态分布或缩放位移t分布充分近似时，即无法应用中心极限定理时，可提供给定包含概率下的包含区间。以下情况会出现不适当的近似:①一个占主导地位输入量的PDF 不是正态分布或缩放位移t 分布;②模型非线性;③使用公式Welch－Satterthwaite 计算有效自由度时，引入的近似误差不可忽略。

5)确定包含区间时无需包含因子。

量器检定规程中给出的玻璃量器容量的数学模型比较复杂，基于以上MCM 方法的特点，在评定其测量不确定度时可以选用MCM 法，本文采用MATLAB 软件编程实现。

2 采用MCM 方法对量器标准不确定度的分析与评定

按照JJG196 －2006 《常用玻璃量器检定规程》的要求，检定方法采用衡量法，通过测量容器内所容纳的工作介质的质量和密度，根据检定规程提供的公式算出被测玻璃量器在标准温度20℃时的实际容量。本文选用100 mL 单标线容量瓶，采用MCM 法对其不确定度进行分析，评定出不确定度结果，其他的可以参照此不确定度分析过程。

2.1 测量模型

检定规程中给出了玻璃量器容量的数学模型，如下所示:

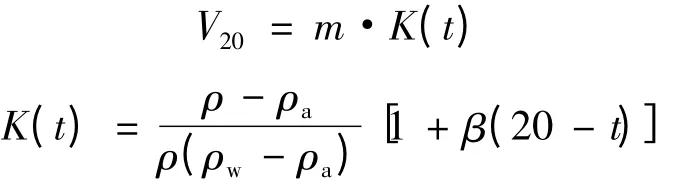
式中:V20为标准温度20℃时的被检玻璃量器的实际容量，mL;ρ 为砝码密度，取8.00 g/cm3;ρa为测定时实验室内的空气密度，取0.0012 g/cm3;ρw为蒸馏水t℃时的密度，g/cm3;β 为被测玻璃量器的体胀系数，℃－1;t 为检定时蒸馏水的温度，℃;m 为被检玻璃量器内所能容纳水的表观质量，g。

模型的输出量为V20，输入量为m，ρa，ρ，ρw，β和t。

2.2 设定概率密度函数PDF

当输入量相互独立时，可根据一系列测量值的分析，或根据某些历史数据、校准数据和专家判断之类的信息所得到的科学判断，为各输入量设定PDF。本例中各输入量服从的分布、最佳估计值以及标准不确定度均列入表1 中。

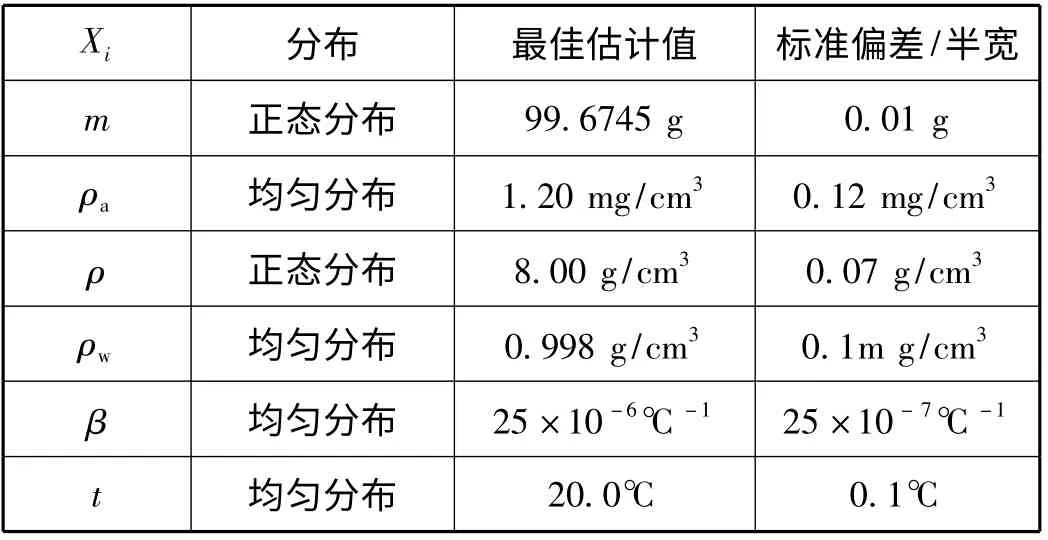
表1 关于量器测量模型的输入量及其概率密度函数

表1 中，水表观质量(m)的相关信息是通过使用衡量法重复测量10 次得到，测量值分别为:99.6752， 99.6893， 99.6682， 99.6723， 99.6710，99.6891，99.6688，99.6705，99.6710，99.6690 g，测量结果平均值和其标准不确定度按下面公式分别计算为

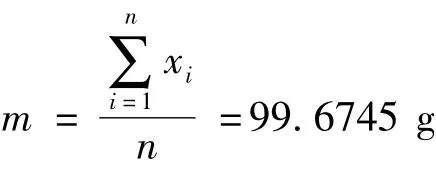
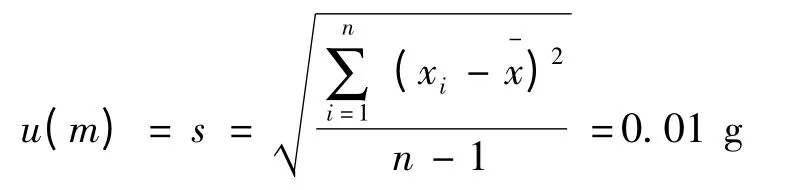
空气密度ρa、体积膨胀系数和温度的相关信息是由JJG196 －2006 《常用玻璃量器检定规程》检定规程得到;砝码的密度信息是通过JJG99 －2006 《砝码》检定规程中给出的典型材料密度表中查表得到;蒸馏水的密度信息是通过查阅资料得到。

2.3 结果报告

在规定的数值容差下MCM 所提供的结果所需的试验次数跟输出量的PDF “形状”及包含概率有关，应合理选择蒙特卡洛试验次数即样本量的大小M，一般情况下取M=106，这样通常会为输出量提供95%包含区间，该包含区间长度被修约为1 或2 位有效十进制数字。应用MCM 法对量器的不确定度进行评定，采用MATLAB 软件进行编程，部分程序如下所示:

clc;clear; %清除MATLAB 中的变量。

M=1000000; %设定蒙特卡洛试验次数。

m=normrnd (99.6745，0.01，1，M); %水表观质量采样值(g)。

ρA= (0.24* rand (1，M) +1.08)* 10^ －3; %空气密度(g/cm3)。

ρB=normrnd (8，0.07，1，M); %砝码密度(g/cm3)。

ρw=0.0002* rand (1，M) +0.9979; %蒸馏水密度(g/cm3)。

β= (5* rand (1，M) +22.5)* 10^ －6; %体积膨胀系数(℃－1)。

t=0.2* rand (1，M) +19.9; %温度(℃)。

V=m. * (rb － ra). * (1 + b. * (20 － t)). / (rb. *(rw－ra));%衡量法数学模型。

s=std (dm); %输出量标准不确定度。

avg=mean (dm); %输出量估计值。

y=sort (dm); %将试验结果从小到大进行排列。

y_ low=prctile (y，2.5); %包含概率为95%时，包含区间的下限值。

y_ high=prctile (y，97.5); %包含概率为95%时，包含区间的上限值。

运行此程序得出100 mL 单标线容量瓶平均值为99.979 mL，标准不确定定度为:0.013 mL;包含概率为95%;包含区间为［99.955 mL，100.006 mL］。

运行程序得到输出量概率密度分布的结果图如图1所示。

3 采用GUM 方法对量器标准不确定度的分析与评定

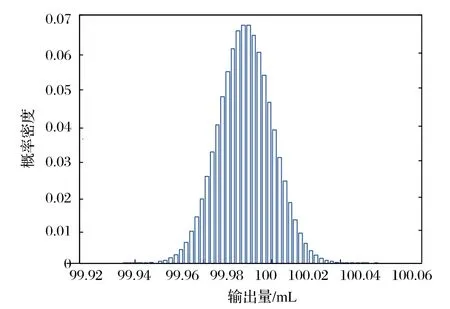
图1 输出量近似概率密度分布图

采用GUM 方法评定量器的不确定度时，数学模型与采用MCM 法评定时的测量模型一致，在此评定过程中，令Dρ=，Dt= 1 + β(20 － t)，则数学模型可以简化为

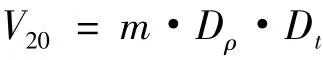
分析此数学模型，得知其不确定度分量包括:①检定点测量重复性引入的不确定度;②质量测量引入的不确定度;③密度引入的不确定度，包括砝码密度、空气密度、水的密度;④温度引入的不确定度，包括体胀系数、温度测量引入的不确定度。

同样的选取100 mL 单标线容量瓶对其不确定度进行分析，灵敏系数由简化后的数学模型直接求得，最后利用表1 中输入量的相关信息评定出其容量平均值为99.978 mL，合成标准不确定度uc= 0.015 mL，包含概率为95%，包含区间为［99.948 mL，100.008 mL］。这一结果比采用MCM 法的评定结果要大，但是均满足玻璃量器规程中的要求。

4 总结

通过采用MCM 法对玻璃量器的不确定度进行了评定，并将此方法的评定结果与GUM 方法的评定结果进行了比较，两者之间虽然存在细微的差异，但是这些结果都满足玻璃量器检定规程的要求。按照JJF1059.2－2012 中使用MCM 验证GUM 的要求，GUM 法通过了验证，在以后进行量器容量的测量不确定度评定时，可以使用GUM 法进行评定。本文主要是以单标线容量瓶为例进行了评定，其他类型的玻璃量器也可依据此方法进行评定，但是在评定的过程中要注意以下几个问题:

1)一般情况下，GUM 方法的评定结果比MCM 方法评定的结果略显保守，这主要是由于在评定过程中，某些不确定度分量被重复计入和计量人员对不确定度分量的理解程度不同造成的。

2)对于滴定管、分度吸量管、量筒、量杯等多刻度线的量器的不确定度评定，应根据用户的需求进行单一刻度线的具体分析，给出该刻度线的不确定度评定结论。

［1］国家质量监督检验检疫总局.JJG 196 －2006 常用玻璃量器检定规程［S］. 2006.

［2］周桃庚. 用蒙特卡洛法评定测量不确定度［M］. 北京:中国计量出版社，2012.

［3］国家质量监督检验检疫总局.JJF1059 －2012 测量不确定度评定和表示［S］. 2012.

［4］国家质量监督检验检疫总局. JJG99 －2006 砝码检定规程［S］. 北京:中国计量出版社，2006.