惯导系统动态校准数据估计算法
2013-04-13李娜娜彭军
李娜娜,彭军
(中航工业北京长城计量测试技术研究所,北京100095)
0 引言
对惯导系统进行动态校准,一方面是为了掌握系统误差规律,建立误差模型,并对系统进行补偿,提高系统的使用精度;另一方面是可以发现系统在设计和制造中的缺陷,为改进系统提供了重要的依据。一般情况下,惯导系统的动态校准是在不同频率的正弦角振动激励下,通过与标准测试台的幅频和相频特性进行对比来实现的,同时还可以得到系统的灵敏度、带宽等动态性能指标。
一些惯导系统输出的角速度量值是有限长数字序列,所以必须对数字序列进行估计,才能得到其相频和幅频特性。大部分惯导系统都是均匀采样的,但是仍有一些是非均匀采样的。因此本文介绍了两种在均匀和非均匀采样状态下都适用的估计算法,给出了惯导系统动态校准时算法选择的建议,以供探讨。
1 曲线估计算法
1.1 正弦信号四参数估计法
基于最小二乘法的四参数估计法是正弦信号曲线[1]拟合常用的算法。这种算法抗干扰性强、精度高、算法简单,适用于对惯导系统动态校准数据的曲线拟合。
设采样序列在tk时刻的估计值为y(k),则拟合后的信号可写为

式中:A0表示正弦信号幅值;ω0表示信号角频率;θ0表示信号相位;C0表示信号直流偏移。
式(1)可以写为
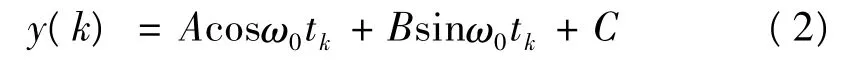
对比式(1)和式(2),有

C=C0
采样序列在tk时刻的值为y0(k),那么真实值和估计值之间的误差平方和:

当已知或估计出信号角频率ω0后,再利用最小二乘法,使式(3)误差平方和取最小,那么得到的信号幅值、相位和直流偏移量就是要估计的三个参数[2]。
正弦信号频率估计的算法有很多,如基于FFT 估计法、相关累加法、遗传算法、BP 神经网络算法等,使用最多的就是频率迭代法。考虑到惯导系统有均匀采样和非均匀采样(即采样时间间隔不等)两种情况,本文利用频率迭代法和最小二乘法相结合的方法估计信号的四个参数,见参数文献[3]。为了更精确地得到信号频率,对测量序列先做DFT 变换,再利用Rife 和Q-Rife 方法估计信号的初始频率[4]。
1.2 直接法
正弦信号四参数估计法在系统均匀采样时准确度很高,但是在非均匀采样且非均匀程度较大时,精度就会下降。另一方面,当系统采样点数多时,四参数估计法耗时比较大。因此为了弥补四参数估计法的不足,在惯导系统校准时也可以采用直接法。直接法也同时适用于均匀采样和非均匀采样。
根据式(1),直接法分段求出测量序列的极值,将各段极值的平均值作为拟合信号的幅值A0,采样序列的均值为正弦信号的直流分量C0,利用相关相位法求相位差。
以下是相关相位法求相位差的原理。
假设原始信号的采样序列为x,测量序列为y,则

当不考虑两信号延迟量时,互相关函数Rxy(τ)只与它们的相位差φ 有关,由此就可以求得两个信号的相位差。因此有
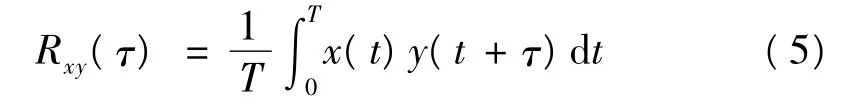
当τ→0 时,有
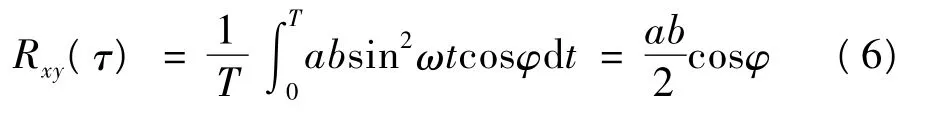
因此
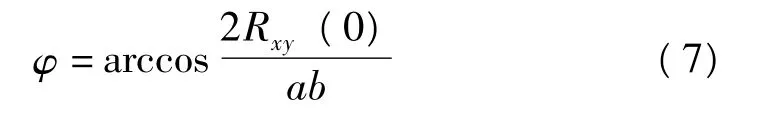
相关相位法求相位差的前提是必须同时采集惯导系统输出信号和正弦激励信号。
2 仿真实验
通过Matlab 工具编写算法并进行仿真:
1)对同一正弦信号进行采样和仿真实验,原始信号的频率均为50 Hz,幅值为1,初始相位为0°,信号中加信噪比为40 dB 的高斯白噪声。
2)设定均匀采样时刻为tk=kTs,k=0,1,…,N-1。其中,Ts=1/fs,fs为采样率。
3)设定非均匀采样时刻为tk=tk-1±iTs,k=0,1,2,…,N-1。其中,Ts=1/fs,i为从[1,3]之间随机选取的一个整数。
4)直接法和四参数估计法的采样时间均为5 s,这样采集的正弦信号周期数相同,在采样率低时采样点数少,采样率高时采样点数多。
2.1 均匀采样的仿真实验
均匀采样时,直接法、四参数估计法两种算法的幅值相对误差、相位差比较见表1。
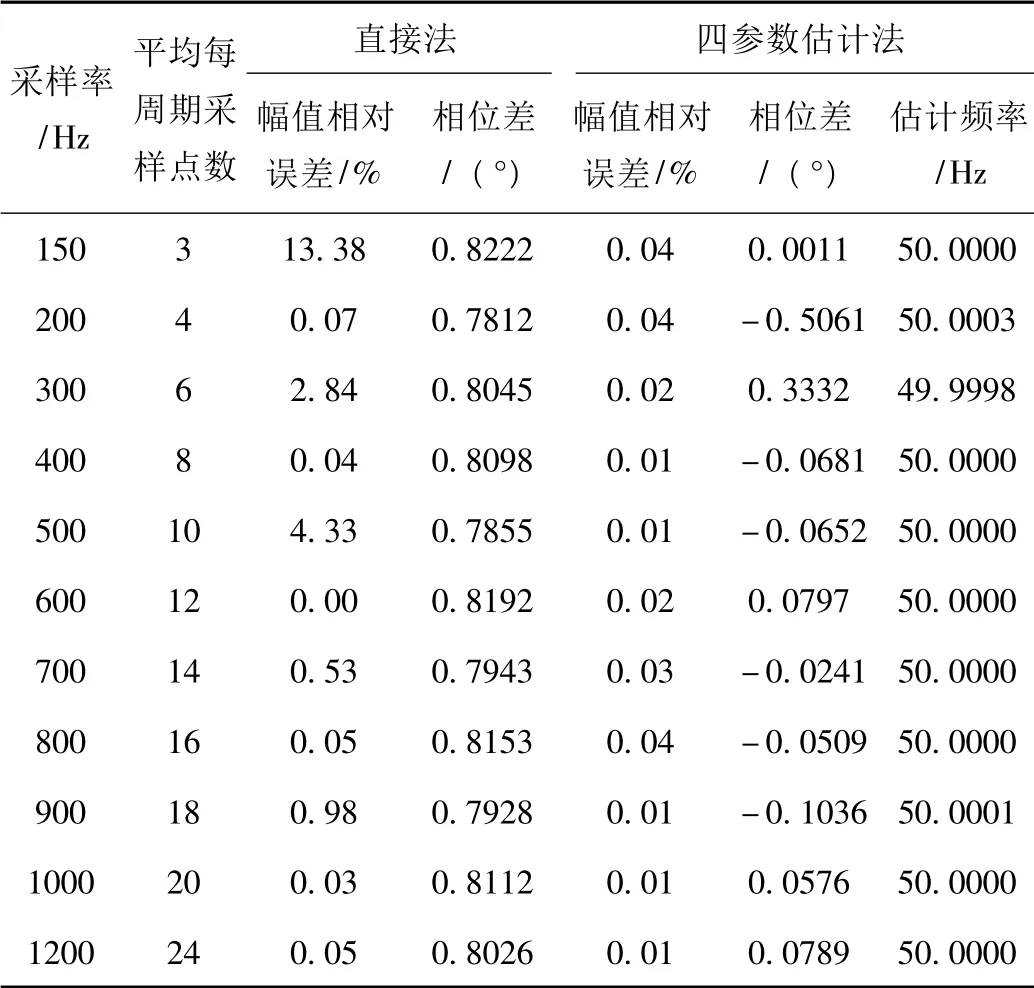
表1 均匀采样50 Hz 正弦信号时的估计结果(幅值相对误差和相位差)
从表1 中可以看出:
1)均匀采样时无论每个周期采样点数多或少(在符合采样定理的条件下),四参数估计法的精度都很高,幅值相对误差不超过0.1%,相位差不超过1°,而且估计的信号频率精度很高;
2)直接法每周期采样点数在10 个以下时,精度不高;采样点数越多,精度越高。
在仿真过程中,信号频率为50 Hz,采样时间为5 s。对于四参数估计法,当采样率为200 Hz 时,采样点数为1000,运算时间为2.27 s;当采样率为1200 Hz 时,采样点数为6000,此时运算时间为57.11 s。可见,采样点数增多,四参数估计法的运算速度变得很慢。相比之下直接法的运算速度很快,无论采样点数多少,运算时间都不超过1 s。
惯导系统在动态校准时要受外界环境噪声和系统自身噪声的影响,两种算法的抗干扰性比较见表2。

表2 均匀采样50 Hz 正弦信号时的估计结果(抗干扰性)
从表2 中可以看出,相比直接法,四参数估计法的抗干扰性强很多。
2.2 非均匀采样的仿真
表3 和表4 分别给出非均匀采样时,两种算法幅值相对误差、相位差和抗干扰性的比较。
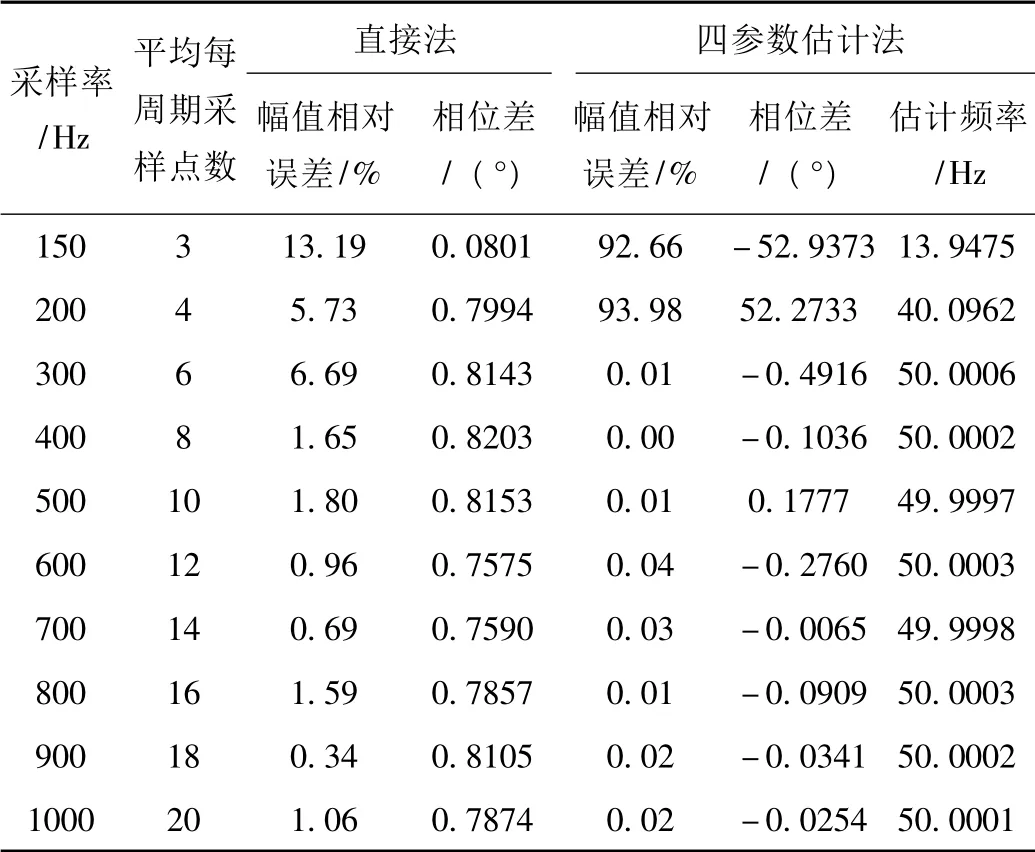
表3 非均匀采样50 Hz 正弦信号时的估计结果(幅值相对误差和相位差)
由表3 可以看出:
1)由于采样非均匀性的影响,当每周期采样点数少时,四参数法的拟合失真度较大;如果每周期采样点数增加,就可以减弱这种非均匀采样的影响,可见四参数估计法受采样非均匀程度的影响较大;
2)非均匀采样对直接法影响不大,采样点数越多,计算精度越高,同均匀采样相同,运算时间基本不超过1 s。
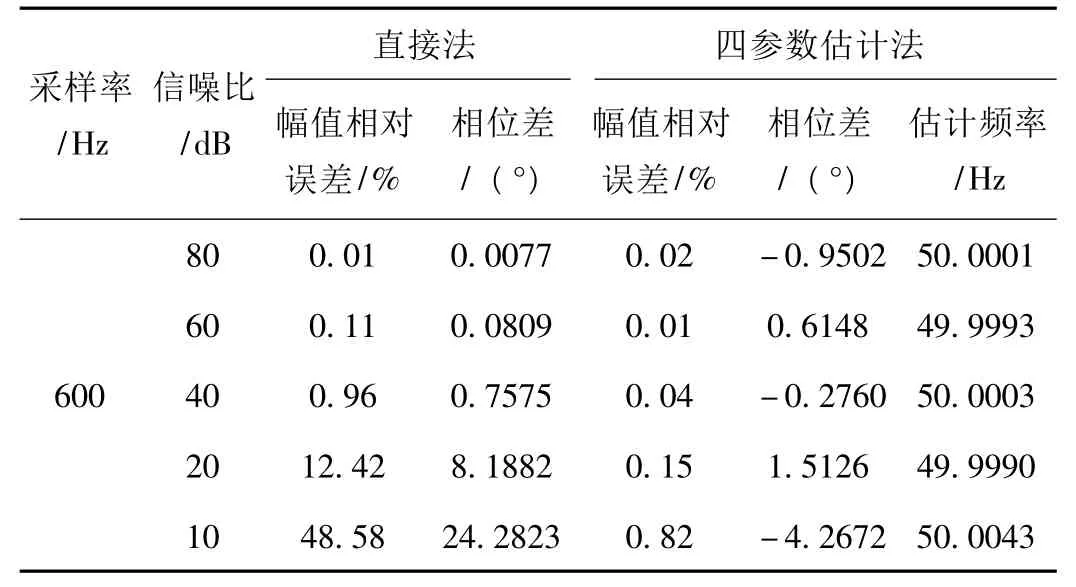
表4 非均匀采样50 Hz 正弦信号时的估计结果(抗干扰性)
从表4 中可以看出,在非均匀采样时四参数估计法的抗干扰性较强。
3 实测试验
用数字存储示波器作为数据采集系统,设定采样速率为1000 Hz。选用信号发生器作为激励,激励正弦信号的幅度为1 V,不同频率下采集5000 个数据点,分别用两种算法对采样数据的幅值进行估算,结果见表5。

表5 用数字存储示波器采样数据的幅值估计结果
从表5 中可以看出,用四参数估计法得到的幅值相对误差明显小于直接法的估计结果。
4 建议
依据仿真实验结果,表6 给出了两种曲线估计算法的适用情况。在对惯导系统进行动态校准时,可根据校准要求和实际校准情况选择合适的估计算法。

表6 惯导系统动态校准曲线估计算法选择的建议
[1]梁志国,孙璟宇.正弦波模型化测量方法及应用[J].航空计测计术,2001,21(6):3-8.
[2]梁志国,张大治,孙璟宇,等.四参数正弦波曲线拟合的快速算法[J].计测技术,2006,26(1):4-7.
[3]吴义华,杨俊峰,程敬原,等.正弦信号四参数的高精度估计算法[J].中国科技技术大学学报,2006,36(6):625-629.
[4]胥嘉佳,刘渝,邓振淼.任意点正弦波信号频率估计的快速算法[J].南京航空航天大学学报,2008,40(6):794-798.
