大体积混凝土温度场一维差分算法探讨

邓旭

(郑州大学 水利与环境学院，河南 郑州 450002)

0 引言

对大体积混凝土而言，控制其温度裂缝的产生和发展是保证混凝土质量的关键，而其温度裂缝则是由于混凝土内部温度场不均匀分布而引起，因此计算大体积混凝土的温度场分布对其温度裂缝控制有重要作用。目前该问题的计算已经有经验公式法、有限元法等［1，2］，经验公式法简单易行，但精度较差，有限元法虽然精度较高，但计算工作量较大。本文以热传导为基础，建立大体积混凝土温度场的一维差分格式，通过对其温度场进行差分求解，其精度可满足工程要求，且计算效率较高。

1 混凝土温度场的热传导理论

1.1 热传导方程

大体积混凝土的热传导问题实际上是固体内有热源的热传导问题，其热传导方程为［1］:

式中，c为混凝土比热，kJ/(kg·℃);λ为混凝土的导热系数，kJ/(m·d·℃);τ为时间，d;ρ为混凝土密度，kg/m3;θ为混凝土绝热温升，x，y，z为混凝土内部点的位置坐标;T为混凝土内部坐标点温度。

1.2 初始条件和边界条件

热传导方程是物体的温度与时间、空间关系，其方程解有无限多，为确定所需要的温度场，还须知道方程的初始条件和边界条件［1］。

初始条件:对于大体积混凝土，其初始温度为其初始瞬时温度，即浇筑温度，为常数。

第一类边界条件:混凝土表面温度T为已知函数，即:

第二类边界条件:混凝土表面的热流量是时间的已知函数，即:

当为绝热边界条件时，∂T/∂n=0。

第三类边界条件:假定经过混凝土表面的热流量与混凝土表面温度T和气温Tf之差成正比。即:

式中，β为混凝土表面的放热系数。

第四类边界条件:当两种固体(接触良好时，则在接触面上温度和热流量是连续的，其边界条件为:

2 一维温度场的有限差分格式

当结构为无限大平板时，其长度和宽度方向远大于其厚度方向，则其热传导方程可简化为一维热传导问题。

一维热传导方程可表示为:

设混凝土板厚为L，将其在厚度方向等分为n－1层，则每层厚度为:

图1 一维差分示意图

设Ti，τ表示第i点在时刻τ的温度，用中心差商代替微商，得:

将式(9)代入式(7)，则可得:

式中，r=aΔτ/h2，当r小于0.5时，差分格式稳定。

边界条件处理:考虑混凝土边界条件多为绝热边界、第三类与第四类边界条件，故对此三种情况建立其差分格式。

绝热边界条件:

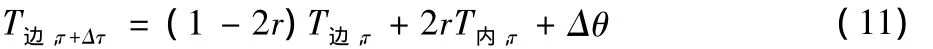
式中，T边为混凝土边界处温度，T内为混凝土内部距离边界为1单位的节点的温度值。

第三类边界条件:利用牛顿后插公式，建立其差分格式为:

式中，s=2βh/λ，T边为混凝土边界处温度，T内1为混凝土内部距离边界为1单位的节点的温度值，T内2混凝土内部距离边界为2单位的节点的温度值，Ta为外界介质温度。

第四类边界条件:

式中，λ1、λ2分别为1、2固体的热传导系数，g1、g2为1、2固体的栅格间距。

3 一维温度场差分求解

某无限大平板，其导温系数为0.1，厚度为10m，初始温度为10℃，两边界温度为0℃［1］。

对于此模型，其温度场理论解为:

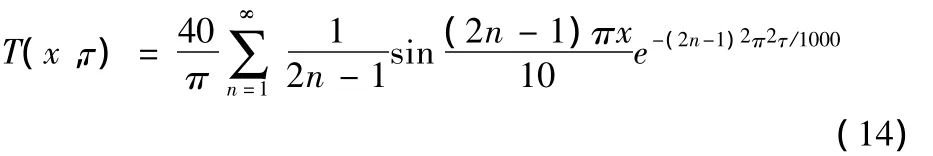
对于无限大平板，可简化为一维问题，对其进行差分求解。由于结构为对称，取一半进行分析，30天后其各点温度值如图2所示。

图2 差分与理论解比较图

取200天对结构进行分析，可得其温度场变化规律为:

图3 温度场变化图

其中心点温度随时间变化规律为:

图4 中心点温度变化规律

通过计算分析，可知差分解与理论解误差较小，其精度可满足工程需要。结构由于散热，整体温度趋于边界温度，其内部点温度下降滞后与边界点，与实际情况相符。

4 结语

建立大体积混凝土热传导的一维差分格式，通过与理论界进行对比，其计算精度也可满足工程需要，但其计算参数的选取对计算精度的影响较大，如果条件允许，应利用试验的方式合理确定各参数取值。

［1］朱伯芳.大体积混凝土温度应力与温度控制［M］.北京:中国水利水电出版社，1999.

［2］王铁梦.上程结构裂缝控制［M］.北京:中国建筑工业出版社，2004.

［3］薛定宇，陈阳泉.高等应用数学的MATLAB求解［M］.北京:清华大学出版社，2008.

［4］杜平，刘书贤，谭广柱，刘魁星.基于四维温度场理论的大体积混凝土数值分析［J］.辽宁工程技术大学学报(自然科学版).2012，31(8):526－530.

［5］严淑敏.大体积混凝土基础底板温度裂缝控制技术［D］.硕士学位论文.浙江大学，2007.

［6］Bofaug Zhu，Ping Xu.Thermal Stress and Temperature Control of Roller－Compacted Concrete Gravity Dams［J］.Dam Engineering，1995，(3):199—220.

［7］Mats Emborg，Stig Bernander.Assessment of Risk of Thermal Cracking in Hardening Concrete Journal of Structural Engineering.1994(10):2893—2910.