基于FEA 分析的大型回转窑等寿命优化
2013-04-09李志刚贾慧芳张文亮
李志刚,贾慧芳,张文亮,王 健
(华东交通大学载运工具与装备教育部重点实验室,江西 南昌 330013)
0 前言
回转窑是对散状或浆状物料进行加热处理的热工设备,该设备是一种重载、超长、多支点、超静定机械运行系统[1-2],广泛用于水泥、冶金、建材、化工等方面。回转窑几何模型如图1 所示。该设备主要由滚圈、筒体、托轮、托轮轴等几个部件组成。

图1 回转窑的几何模型Fig.1 Geometry model of rotary kiln
在生产过程中,回转窑的运行轴线会偏离理论轴线,容易出现以下故障:筒体产生疲劳裂纹,严重时会产生塑性变形,甚至断裂[3];筒体内衬的耐火砖脱落导致红窑[4];传动系统和支承装置存在附加载荷和冲击载荷,容易出现轴瓦发烧现象,甚至发生托轮轴断裂[5]。这一系列问题是由于回转窑在各档位上载荷分配不均,筒体的轴线不平直而引发的。在回转窑的日常维护中,通常情况下是对回转窑的调整来实现的。通过对回转窑托轮与滚圈支承角的合理调整可以使回转窑设备处于更好的工作状态,以此实现设备的运行健康维护。
支承角经过调整后,回转窑系统不可能将载荷分配调整到完全均匀,同时各部件在不同位置的疲劳强度不同,受到的疲劳损伤不一致,剩余疲劳寿命也不一样。研究发现[3-6],所有关键部件寿命相等的情况下,回转窑整体系统的寿命最长。因此,回转窑所有关键零部件剩余疲劳寿命相等是回转窑最佳运行状态的重要标志[7-8]。
1 回转窑模型有限元分析
在ANSYS 中,采用Solid70 三维热实体单元对回转窑模型进行分析。该单元具有8 个节点,每个节点一个温度自由度,适合于包含热实体单元,同时还需在热实体单元分析基础上进行结构单元分析的模型[9]。
以回转窑整体模型为研究对象进行热力耦合场计算,图2 是回转窑整体模型在耦合场下的应变云图,由图可知筒体在第一档与第二档滚圈中部的变形最大,最大值为8.355 mm。图3 是整体模型在耦合场下的应力云图,由图可知回转窑整体模型应力的最大值为171 MPa。


2 建立各部件疲劳寿命模型
根据Miner 疲劳损伤累计法则,回转窑设备各部件经过N 次循环后的疲劳损伤量D 的计算公式为[6]:
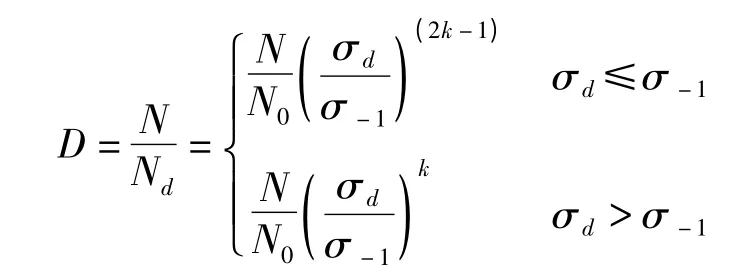
式中,σ-1为各部件材料的疲劳极限;N0为对应疲劳极限下的循环次数;Nd为应力σd作用下的极限循环次数;K为材料的疲劳特性常数。
通过回转窑模型未做调整前的工作时间,可以估算出各部件的在应力σdg作用下的循环次数N。

式中,T为各部件未做调整前的工作时间;t为各部件每旋转一周所用的时间。
根据Miner 疲劳损伤累计法则,计算出回转窑各部件经过一定时间运行后,各部件的疲劳损伤量Dd。
在当量应力σd作用下,单次循环损伤量的公式为:
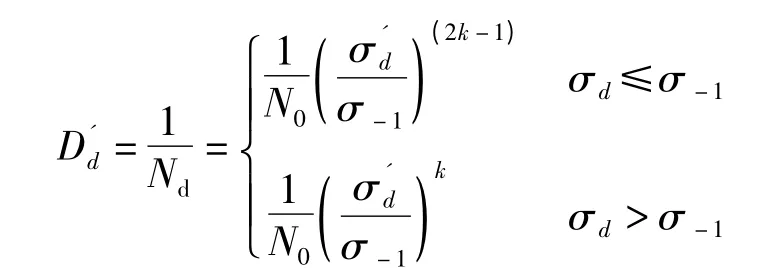
回转窑各部件的剩余疲劳寿命λmg:
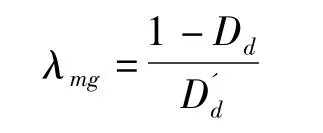
回转窑各部件的剩余寿命T'(单位为年)为:

式中,n为回转窑各部件每分钟的转速;D为回转窑各部件平均每年运行的天数。
3 建立多目标集成优化的模型
3.1 设计变量
由于支承角的不同,各个支承系统的疲劳损伤是不一致的。支承角度的改变,会使回转窑运行时轴线发生变化,这样支承系统的应力应变均发生变化。本文以托轮对滚圈的支承角jd1,jd2,jd3,jd4为设计变量,对滚圈与托轮的支承角进行优化。
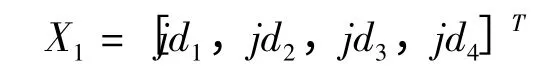
式中,jdn为第n 档滚圈与托轮的支承角。
3.2 目标函数
在回转窑运行过程中,滚圈承受着筒体的全部重量,并且对薄壁筒体起着加固作用。滚圈的体积大,在制造、运输和安装过程中都有较高的技术要求,因此以滚圈的剩余寿命最长为第一目标函数:

式中,Tgn为第n 档滚圈的剩余寿命。
由于重压及过盈配合的双重作用,托轮轴在配合面端部和轴肩处产生了应力集中。一旦托轮轴塑性变形累积量达到材料极限值,将会导致突发性断裂,对生产会造成巨大的损失。因此在保证滚圈寿命最优的情况下,以托轮轴的剩余寿命最长为第二目标函数:
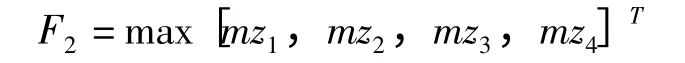
式中,mzn为第n 档托轮轴的剩余寿命。
在同时满足目标函数一和目标函数二的情况下,以托轮的剩余寿命最长为第三目标函数:

式中,mtn为第n 档托轮的剩余寿命。
为了使各档滚圈的寿命尽可能相当,也就是滚圈寿命的绝对值之差最小,所以将任意两档滚圈寿命之差的绝对值作为第四目标函数,即:

式中,Tgi为第i 档滚圈的剩余寿命;Tgj为第j档滚圈的剩余寿命。
为了使每档上托轮轴的寿命尽可能相当,将任意档托轮轴寿命之差的绝对值作为第五目标函数,即
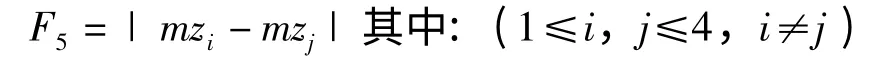
式中,mzi为第i 档托轮轴的剩余寿命;mzj为第j 档托轮轴的剩余寿命。
为了使各档托轮的寿命尽可能相当,将任意两档托轮寿命之差的绝对值作为第六目标函数,即

式中,mti为第i 档托轮的剩余寿命;mtj为第j档托轮的剩余寿命。
3.3 约束条件
(1)支承角。为了使滚圈支承在托轮上,支承角度应满足[6]:

式中,RT为托轮的半径;RG为滚圈的半径。
在传统设计中,托轮对滚圈的支承角一般都设为30°,在保证计算精度不变的情况下,为了减少试验次数,设20°≤jdn≤40°.
(2)轴线偏差。回转窑运行中滚圈变形偏离理想轴线太大会导致耐火砖脱落,严重时会使筒体出现裂痕甚至断裂。因此,滚圈的椭圆率不能超过极限值,一般将该值定为2‰。

(3)最大接触应力。滚圈和托轮的接触应力保证不超过最大接触应力即:

(4)各优化目标的最小寿命值。
为了保证各优化目标的寿命相当,对滚圈与托轮在支承角为30°时各优化目标的寿命进行分析后,将滚圈、托轮、托轮轴的最小寿命定为不得小于5 年,这样可以减少试验的计算步骤,计算的精确度也不会受到影响。

3.4 试验模块
该试验设计框架中包括2 大模块,如图4所示。
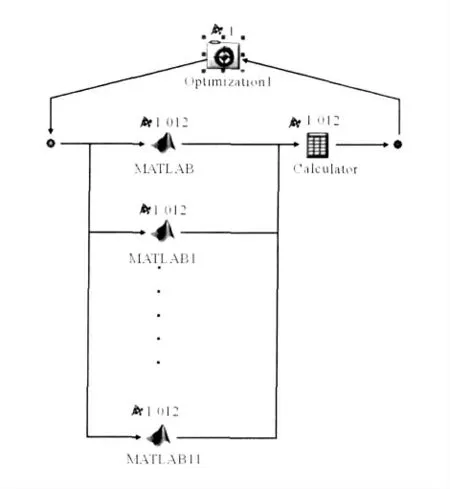
图4 Matlab 集成流程图Fig.4 Flow chart of Matlab integration
(1)Matlab 模块。将滚圈与托轮支承角的角度值作为输入变量,提供支承角参数,通过角度值的变化实现对回转窑模型支承角度的修改。各档滚圈、托轮、托轮轴寿命作为输出文件,得到各目标的最优寿命;
(2)Calculator 模块。通过计算器来实现对约束条件、目标函数取值范围的控制和对目标函数进行求解;
(3)Optimization。按照前述部分的要求设定各变量的初始值、变化范围、约束条件和目标函数;设置运行的最大次数(预估值)为1000,设置收敛系数为1.0E-8,该值表示每次执行的可行解和目前为止的最优解之间的最大差值。
3.5 优化算法
模拟退火法[10]是将组合优化问题与统计力学中的热平衡问题类比,从初始点开始每前进一步就对目标函数进行一次评估,只要函数值下降,新的设计点就被接受,反复进行,直到找到最优点。
本文运用模拟退火算法之前主要考虑以下几个方面:
(1)在Isight 软件中,模拟退火法可以对最大运算次数进行预估;同时可以对每次执行的可行解和目前为止的最优解之间的最大差值进行设置,保证了计算的精确度;
(2)在本试验中,一共有12 个Matlab 程序,模拟退火算法可以处理任意的系统和目标函数并能有效探索全局优化解,通常具有较好的收敛性;
(3)在本试验中,将滚圈与托轮在各档位上的支承角作为设计变量,模拟退火算法适合处理实数型、离散型设计变量,适合处理连续和非连续空间。
4 优化结果分析
4.1 支承角变化趋势分析
以回转窑第一档支承角在寻优过程中的变化趋势为例,如图5 所示。在变化趋势图中,可以看出各档支承角在经过1012 次迭代循环最终收敛。图中箭头所指的点表示优化过程中寻找到各档支承角的最优解。第一档至第四档最佳支承角分别为35.075°,33.01°,33.576°和34.063°。
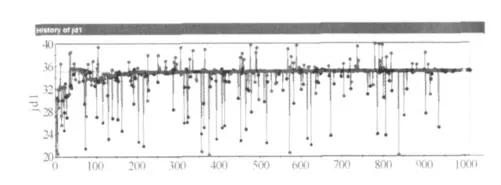
图5 第一档支承角寻优过程中的变化趋势Fig.5 Changing trend in first supporting angle searching process
4.2 模型各参数的频率灵敏度分析
图6为第一档至第四档支承角优化结果频率灵敏图,从图中可以看出第一档至第四档支承角分别在35.075°,33.01°,33.576°和34.063°附近出现频率最大,分别达到663 次,440 次,549 次和581 次。可以将其视为各档的最佳支承角。

图6 各档支承角优化结果频率灵敏图Fig.6 Sensitivity analysis chart of optimization result each supporting angle
4.3 模型集成结果分析
模型迭代循环计算,得到支承角和各部件寿命优化结果值如图7 所示,第一档至第四档滚圈剩余寿命分别是9.176 年,6.537 年,6.554 年和6.895 年。第一档至第四档托轮轴寿命分别是5.273 年,6.537 年,6.554 年和6.895 年。第一档至第四档托轮寿命分别是9.176 年,7.742年,6.763 年和6.374 年。各部件剩余寿命第一档滚圈寿命由优化前的7.05 年提高到到9.18年,提高了2.13 年。优化后第二档到第四档滚圈分别提高了0.5913 年,0.6836 年和0.9442年。优化后滚圈的平均寿命比优化前寿命提高了17.49%。同样的方法可以得出:托轮轴优化后的平均寿命比优化前寿命下降了27.6%,托轮优化后的平均寿命比优化前寿命下降了32.9%。

图7 支承角和第一至第三目标函数优化前后结果Fig.7 Results before and after optimization of supporting angle and the first target to third target functions
第四目标至第六目标函数优化前后结果值如图8 所示,滚圈各档寿命与第一档滚圈寿命之差平均减少了1.36 年。第一档托轮轴与各档托轮轴平均寿命差平均减少了0.7566 年,第一档托轮与各档托轮平均寿命差减少了2.60 年,下降幅度达到58.2%。在第一档滚圈与第一档托轮和托轮轴之间平均的寿命差减少了,下降幅度达55.07%,达到了等寿命优化的目的。

图8 第四目标至第六目标函数优化前后结果Fig.8 Results before and after optimization of fourth target to sixth target functions
5 优化前后模型对比分析
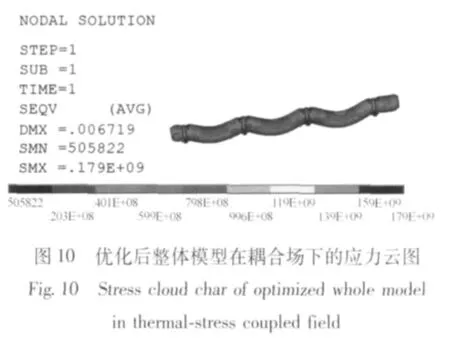
图9 和图10 分别是优化之后整体模型在耦合场下的应变云图和应力云图,结合图2、图3,通过优化前后对比可知,筒体第一档与第二档之间的变形由8.35 mm 下降到6.719 mm,下降幅度达到19.5%。第二档与第三档之间的变形由7.426 mm 下降到5.973 mm,下降幅度达到19.566%。第三档与第四档之间的变形由6.498 mm 下降到了 5.226 mm,下降幅度达到19.575%,分析得出经过优化调窑后筒体直线度有所改善。

6 结论
(1)通过对回转窑整体模型进行热力耦合场的分析可知,回转窑模型在两档位之间的变形最大,同时两档位之间的变形量不相同,该变形量对筒体直线度的好坏有很大影响,同时反映出回转窑各档载荷分配不均,筒体的直线度有待优化;
(2)通过对回转窑各档位支承角优化结果得出,各档位支承角频率优化点集中出现在33°到35°之间,说明要使回转窑各部件的剩余寿命尽可能相等,各档滚圈与托轮的最佳支承角必须在此区间内。同时说明,传统设计中支承角定义为30°并不合理。在日常维护中,需对回转窑支承角的调整引起重视;
(3)通过对优化前后回转窑模型进行有限元分析结果对比可知,筒体最大变形由8.35 mm下降到6.719 mm,优化调窑后筒体直线度有所改善,回转窑模型的最大应力值有所增大,但增幅很小,优化结果也满足回转窑强度要求;
(4)通过优化前后的数据对比可知,优化后滚圈寿命有了较大幅度的提高,虽然托轮和托轮轴的寿命的有所下降,但是差下降幅度在50%以上各部件的平均寿命,回转窑各部件的寿命值更加均衡,优化结果实现了等寿命优化的目的。
[1]王琳,王炳龙,陆大刚,等.大型回转窑筒体装置有限元分析研究[J].水泥工程,2010(2):48-54.
[2]王和慧,谢可迪,陈一凡,等.大型回转窑筒体结构的力学行为分析[J].机械强度,2010,32(4):606-616.
[3]Yoshitsugu Kimura,Masami Sekizawa,AkioNitanai.Wear and fatigue in rolling contact[J].Wear.2002,253:9-16.
[4]李学军.大型多支承回转窑健康维护理论与技术研究[D].长沙:中南大学机械电子工程学院,2003.
[5]肖友刚,陈志刚,袁英.斜压状态下回转窑托轮接触疲劳寿命预测[J].兰州理工大学学报,2007(7):165-167.
[6]肖友刚.多支承回转窑接触体系的力学特征研究及参数优化[D].长沙:中南大学,2004.
[7]K.Pazand,M.Shariat Panahi,M.Pourabdoli.Simulating the mechanical behavior of a rotary kiln using artificial neural networks [J].Materials & Design,2009,10(9):3468-3473.
[8]洪元.大型回转窑支承构件滚动接触应力场和疲劳寿命的研究[D].长沙:中南大学机械电子工程学院,2007.
[9]王泽鹏,张秀辉.ANSYS 12.0 热力学有限元分析从入门到精通[M].北京:机械工业出版社,2010.
[10]赖宇阳.Isight 参数优化理论与实例详解[M].北京:北京航空航天大学出版社,2012.
