四支撑装置稳定性研究及应用
2013-04-09李建涛李继波
李建涛,李继波
(三一重工股份有限公司泵送研究院,湖南 长沙 410100)
0 前言
四支撑装置广泛运用于起重机、登高车、泵车等各类机械中,是一种连接工程机械底盘,并起支撑作用的结构(图1)。该支撑装置具有结构简单、布局方便的特点,能为上装在水平方向360°范围内工作提供支撑。
四支撑装置的稳定性一直是工程机械的研究热点[1]。学者们提出了多种稳定性判据[2-5],并致力于优化各支撑的结构与布局[6],以提升整车稳定性。然而,多数判据只强调了某个稳定性指标,未综合考虑整车的受力、支承、变形对稳定性的影响以及对操作者感官的影响,因为参考因素的单一难以避免发生整车失稳的故障[7-8]。
本文提出采用主观评价方法与客观评价方法相结合的方式,对四支撑装置稳定性进行综合判定,并采用最小二乘法与最小包络圆法对试验数据进行处理,能提升试验精度,提高稳定性判断的准确性。
1 稳定性评价方法
稳定性评价方法包括主观方法与客观方法两类,主观评价方法是指支撑装置的工作姿态带给操作者的感官,本文通过大量研究,总结出三项用于主观评价的指标;客观评价方法是指不能被操作者直观感知,需要通过计算核定稳定性的方法。
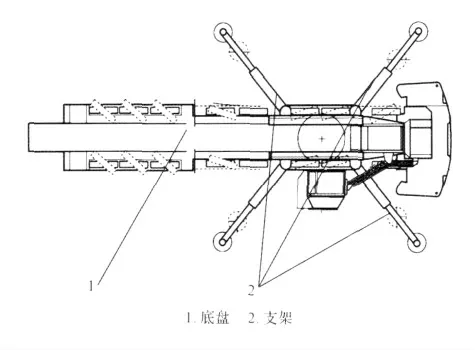
图1 四支撑装置结构示意图Fig.1 Structure diagram of four-supported device
1.1 主观评价方法
(1)支撑装置横梁的变形量a。该值反映支撑装置的整体刚性,刚性不足是稳定性不够的直观感受之一,变形量a 越大,主观感受的稳定性越差。

图2 四支撑装置横梁变形示意图Fig.2 Beam deformation of four-supported device
(2)支撑装置立柱的倾斜量b。该值反映支撑装置的刚性对整车的影响,倾斜量b 越大,主观感受的稳定性越差。
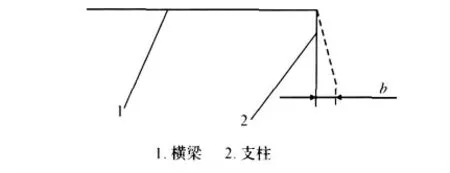
图3 四支撑装置立柱变形示意图Fig.3 Deformation diagram for stand column of four-supported device
(3)支撑装置的抬起量c。机械设备工作时,常常出现三点支撑的情况,此时未着地的支撑的离地高度就是抬起量。不同类型的设备对稳定性的要求不同。火箭发射车要求四支撑全部着地,不允许三点支撑[9];混凝土泵车一般要求单腿抬起高度不超过200 mm[10]。
1.2 客观评价方法
(1)稳定性系数k。通过对各部件称重,确定其重心位置和重量,通过静态稳定系数来度量整车稳定性[11]。

式中,M稳为整机由自身重力产生的反倾翻力矩;M倾为上装部分及载荷产生的倾翻力矩。
(2)第二最小支反力FSCMin。建立如图4 所示的坐标系,A、B、C、D 分别代表四支撑处于的位置;O 点为上装旋转中心;O'为下装(除上装以外的其他部分)重心位置;G 代表下装自重。将上装对旋转中心O 点的作用简化分解为集中载荷P 和力矩M,力矩M 与x 轴正向夹角为θ。
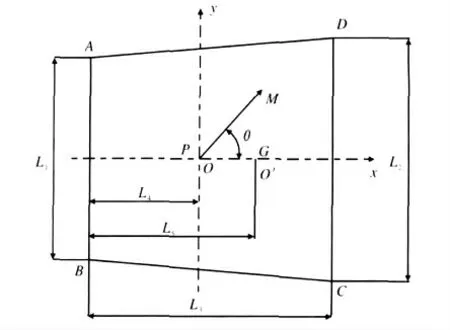
图4 四支撑装置结构示意图Fig.4 Structure diagram of four-supported device
计算出四个支撑点在竖直方向的受力为FA、FB、FC、FD[12],第二最小支反力FSCMin 是指上述4 个力中第三大的力。
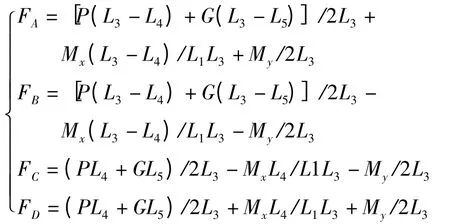
(3)重心圆距倾覆线的距离L。整车重心随上装部分的转动而变化,根据文献[13]所述,整车重心构成一个圆,即重心圆,而各支撑点的连线构成倾覆线。重心圆位于倾覆线内,整车稳定。根据图5,列出力矩平衡方程

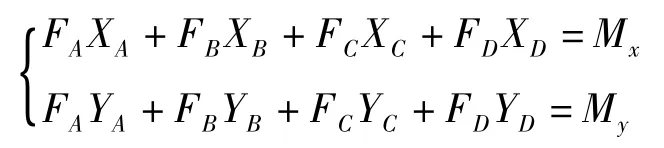

图5 重心圆结构示意图Fig.5 Structure diagram of gravity center circle
根据式(1)可确定该状态下整车重心位置(x1,y1)。获取上装在最恶劣工况不同方向下的三个重心位置(xi,yi),i=1、2、3,通过三点可由公式(x-a)2+(y-b)2=R2确定整车重心圆(图5)。重心圆与倾覆线的距离,L=min(L1,L2,L3,L4)。
2 稳定性分析
根据稳定性评价理论,对某四支撑装置进行有限元仿真,获取支撑装置各部分变形与支反力,进行稳定性分析。该四支撑装置参数如表1所示。

表1 四支撑装置参数表Tab.1 Parameters of four-supported device
建立该装置的有限元模型,获取上装在正后、正前、正右方向时,各支撑点支反力见表2。将表2 的数据代入公式,求出三种工况下对应的圆心坐标,代入公式(x-a)2+(y-b)2=R2中,得到a=4456、b=4205、R=3943 的值,计算出L 值。
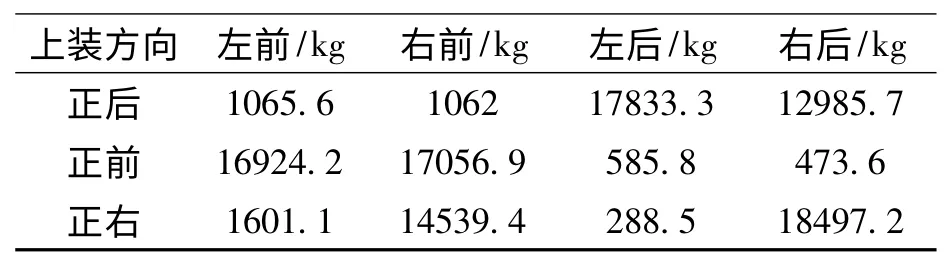
表2 三种工况的支反力Tab.2 Reaction forces for three working conditions
因此,重心圆方程为(x-4456)2+(y-4205)2=39432,绘制重心圆如图6 所示。该四支撑装置的重心圆位于倾覆线内,重心圆与倾覆线最小距离L为235 mm,位于整车正前方。
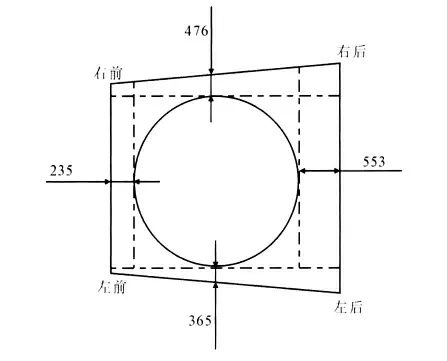
图6 重心圆示意图Fig.6 Schematic diagram of gravity center circle
根据有限元仿真结果,获取各支撑的变形与支反力,其他各主要评价指标的结果见表3。

表3 稳定性评价指标有限元分析结果Tab.3 FEA results for stability evaluation indexes
3 试验测试与分析
3.1 试验方法
稳定性试验时,主观评价三指标可通过直接测量获得;稳定性系数k 通过对各部件称重,确定其重心位置和重量来计算;第二最小支反力和重心圆距倾覆线距离L 需要通过称重传感器获取各支撑点的受力。
试验数据常常受到称重传感器的零飘以及信号干扰的影响,为提升试验精度,一般尽可能多地试验“最不利”的工况,评价指标a、b、c、k、FSCMin 取多组试验的最值,而L 值需要根据重心圆确定。三组试验数据能绘制一个重心圆,不同的试验数据绘制出的重心圆之间存在一定差异。为合理规避测试误差,采用最小二乘法或者最小包络圆法绘制重心圆,判定整车稳定性。
3.2 最小二乘法
最小二乘法是一种曲线拟合的方法,通过最小化误差的平方和寻找数据的最佳函数匹配[14]。即
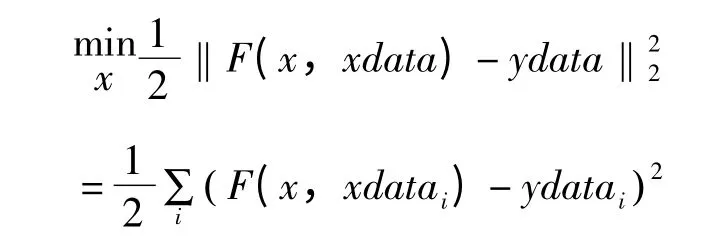
通过测试数据可以得到各种工况下整车重心坐标[x,y],即

将坐标代入重心圆公式(x-a)2+(y-b)2=R2,利用最小二乘法原理,即求最小,分别求此函数对各变量的偏导,通过方程获取最优的(a,b,R),即

试验测得上装位于8 个不同方向的整车重心坐标为

采用最小二乘法绘制整车重心圆结果如图7所示。结果表明:8 个方向拟合出的重心圆比3个方向更精确,但是仍有部分点处在重心圆之外,对于工程设计来说不够保守。
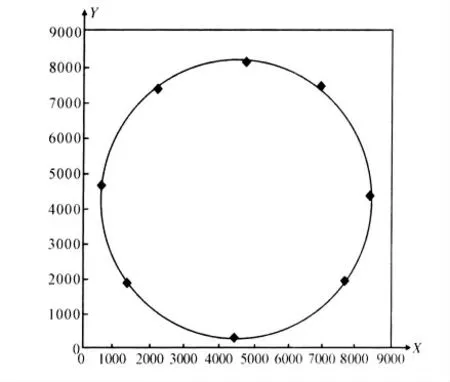
图7 最小二乘法拟合重心圆Fig.7 Gravity center circle fitted by least square method
3.3 最小包络圆法
最小包络圆法的思想是确定一个包括了所有试验点重心坐标的最小圆。如上述8组坐标,任取3组绘制圆,可获得=56 个重心圆。根据3组重心坐标,由重心圆公式,可求得圆O'的参数(a',b',R'),比较其他坐标点是否位于该圆内部,若该圆满足R'≥则保留该圆。
最后比较所有保留圆的大小,取半径最小的圆最为最小包络圆。
对8组重心坐标,按照最小包络圆法绘制的重心圆如图8。结果显示:该圆包括了所有的测试点,按该圆进行稳定性判定安全性更高。
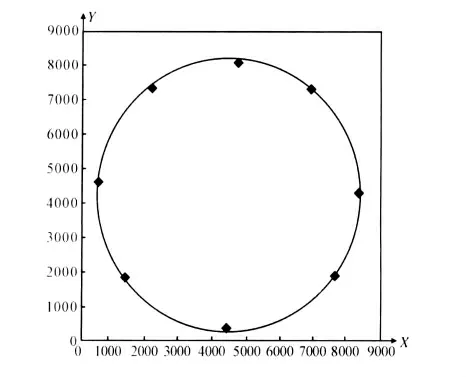
图8 最小包络圆法拟合重心圆Fig.8 Gravity center circle fitted by minimum envelope circle method
3.4 试验结果
根据上装在8 个最恶劣姿态下的测试结果,支撑装置横梁的变形量a、支撑装置立柱的倾斜量b、支撑装置的抬起量c 取最大值,稳定性系数k、第二最小支反力FSCMin、重心圆距倾覆线的距离L 取最小值,结果见表4。

表4 稳定性评价指标试验结果Tab.4 Test results for stability evaluation indexes
如图9 所示,各指标的试验值与仿真值吻合较好,证明上述方法能较好反映支撑装置的稳定性。
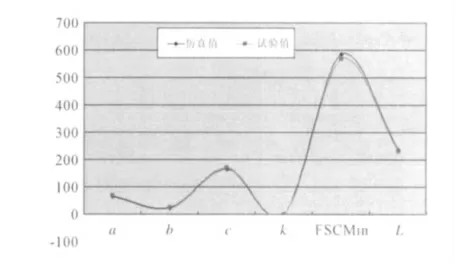
图9 稳定性指标结果对比Fig.9 Comparison of stability evaluation indexes
4 结论
(1)提出了基于主观与客观结合的稳定性评价方法,理论推导了各指标的计算依据。
(2)通过仿真和试验两种方法,将上述指标运用于某四支撑装置的稳定性分析中,结果显示,各指标能准确反映装置的稳定性状况。
(3)通过主观评价方法,能提供更安全的现场操作体验,通过客观评价方法特别是实时采集各支腿反力,能为整车进行稳定性监测与预警,保证四支撑装置的工作安全性。
[1]刘东.考虑大变形因素的高空作业车倾覆稳定性研究[D].大连理工大学,机械电子工程,2011.
[2]MoGhee R,Frank A.On the stability properties of quadruped creeping gaits[J].Math Biosc,1968(3):331-351.
[3]McGhee R B,Iswandhi G I.Adaptive locomotion for amultilegged robot over rough terrain[C].IEEE Trans on Systems,Man,and Cybernetics,1979,9(4):176-182.
[4]Song S-M,Waldronk J.Machines thatwalk:adaptive suspension vehicle[M].MIT Press,1989.
[5]Zhang C,Song S-M.Gaits and geometry of awalking chir for the disabled[J].J Terramechanics,1989,26(3/4):211-233.
[6]姜校林,欧沩滨.混凝土泵车支腿展开角度的优化设计[J].建筑机械,2005(5):75-76.
[7]梁淇洪.浅析汽车起重机的失稳及失稳的预防措施[J].装备制造技术,2010,1:173-174.
[8]施康,邹春曦.工程车辆作业稳定性试验研究[J].机械设计与制造工程,2000,11:38-39.
[9]张胜三.发射车支腿反力及稳定性计算[J].导弹与航天运载技术,1994,3:18-24.
[10]康辉梅.混凝土泵车支腿反力与抬起量分析[J].建筑机械技术与管理,2002,4:7-10.
[11]江海燕,高金花.汽车起重机稳定性影响因素分析[J].现代机械,2009,1:50-52.
[12]张艳伟,孙国正,石来德.混凝土泵车支腿反力计算及基于ANSYS 的支腿结构分析[J].中国工程机械学报,2004,7:253-258.
[13]姜校林.关于混凝土泵车稳定性的几点思考[J].建筑机械化,2006,7:28-30.
[14]玛蒂尔达.数值方法(MATLAB 版)[M].北京:电子工业出版社,2002,6:196-201.
