基于地震图像校准的共成像点道集增强技术

李钟晓，陆文凯，王 季

清华大学自动化系 智能技术与系统国家重点实验室 清华信息科学与技术国家实验室（筹），北京 100084

1 引 言

在理想情况下经2D 叠前偏移生成的共成像点道集（Common Image Gather，CIG 道集）对应于相同的地质地层位置．我们期望CIG 道集中的各道保持高度的一致性，然而由于偏移速度误差、各向异性等的影响，地质构造并没有正确的成像．实际成像点在水平和垂直方向上会偏离真实成像点，导致CIG道集中的地震同相轴没有得到有效拉平．由共成像点道集抽取的共偏移距道集（Common Offset Gather，COG 道集）可当成相同地下成像的多个观测．COG道集上各实际成像点存在的水平和垂直错位，会降低叠加剖面的分辨率，并导致地震属性分析和地震反演精度的降低．

到目前为止，已经提出许多道集拉平方法［1－13］来消除叠前地震道集（如共中心点道集（Common Middle Point，CMP道集）或CIG 道集）中各点的垂直校正量（剩余时差），提高叠加剖面的分辨率．基于互相关的方法［1－9］通过计算待校正地震道和模型地震道的互相关来自适应估计和消除垂直方向的校正量；以相位替换为基础的方法［10－13］是根据信号到达时完全包含在信号相位谱的理论，首先计算模型道的相位谱，然后对待校正道的相位谱进行替换来完成垂直校正量消除．这些方法能有效消除垂直方向各个成像点与真实成像点的错位，但忽略了水平错位对叠加质量的影响．另外，动校正后的CMP道集或叠前偏移后的CIG 道集中的局部相关值作为叠加道的加权系数，能有效提高地震数据叠加的信噪比和成像精度［14－15］．Perez等将图像校准技术应用在3D 叠前偏移数据的时间切片上，来消除叠前偏移数据中的水平校正量［16］．但经过高精度偏移速度分析后，CIG 道集仍然会存在未拉平的同相轴而产生垂直方向的剩余时差［2］．如何有效地同时估计并消除COG 道集中存在的垂直和水平校正量，提高CIG 道集同相轴的一致性，成为值得研究的问题．

本文利用地震图像校准技术对2D 叠前偏移后的COG 道集各点进行校正，同时消除COG 道集的水平和垂直扰动量，增强CIG 道集同相轴的一致性和叠加结果的分辨率．图像校准技术［17］是一种用来进行图像变换的数学工具，被广泛应用在医学成像和计算机图形学等领域［18－19］，用来拾取和消除不同图像之间的扰动量．在石油物探领域，图像校准技术用 来监测时移油藏变化［20－25］和评价AVO 分析中的不确定性［26］等．本文方法将叠加剖面作为模板道集，计算各个COG 道集和模板道集的局部2D 互相关值，同时假设互相关值随2D 相对移动量的变化满足连续凸函数，通过计算互相关函数的最大值来估计COG 道集中各点的水平和垂直校正量．为消除计算误差的影响，需要对估计的2D 校正量进行加权均值滤波处理．与传统的基于互相关的剩余时差消除方法［1－9］或水平校正量消除方法不同［16］，本文在水平和垂直方向计算2D 互相关最大值对应的水平和垂直校正量，并在亚像素域估计正确的成像点幅值．基于互相关的自动统计剩余静校正方法应用在野外静校正之后，消除由于地形突变、风化层基底和风化层速度变化所造成的走时畸变．所估计校正量与采样时间无关，只与空间位置有关，每道估计一个时延量并进行剩余静校正量消除［27］．本文方法应用在2D 叠前偏移之后，消除由于偏移速度误差、偏移算法等造成的水平和垂直错位．所估计的校正量与COG 道集各点的空间和时间位置有关．

下面首先介绍图像校准技术的基本原理，然后给出叠前道集水平和垂直校正量消除的算法流程图，最后采用所提方法处理模型数据和实际数据，并与传统基于互相关的垂直校正量［2－4］消除的效果进行对比．

2 基本原理

由于偏移误差的影响，COG 道集中实际成像点在水平和垂直方向偏离真实位置，如图1所示．图像校准技术将待校正道集（共偏移距道集）与模型道集进行匹配，来逐点估计水平和垂直校正量．考虑到信噪比要求，模型道集通常选择为CIG 道集中近偏移距到中偏移距的部分叠加［4］．由于对COG 道集各点估计的水平和垂直校正量往往位于非整数位置，因此需要对COG道集进行重采样估计真实的成像点振幅．

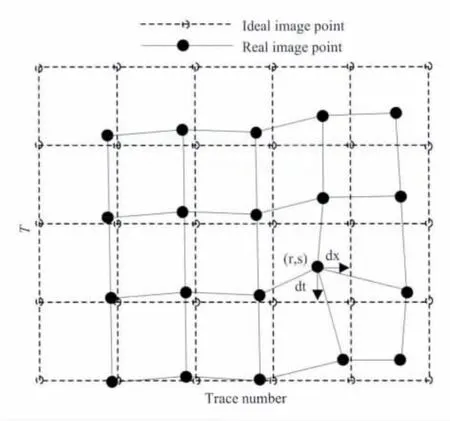
图1 实际成像点和理想成像点的关系Fig．1 The relationship between the real image point and the ideal image point

在本文方法中［dt（r，s），dx（r，s）］代表所估计的垂直校正量和水平校正量，即图1中实际成像点偏离真实成像点的垂直和水平位移，r，s分别代表实际成像点的时间和空间位置．如果gb（r，s）表示待校正道集，校正后道集ga（r，s）可以表示为：

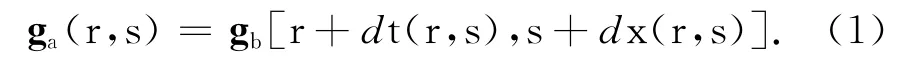
垂直校正量dt和水平校正量dx与输入道集中成像点的位置r，s有关．输入道集和模型道集的局部互相关可被用来衡量两个道集在该点的相似性．图2描述了地震图像校准的基本原理．a图表示待校正道集（上）和模型道集（下），以待校正道集中的某点为中心开窗（图b），计算待校正道集和模型道集在该点不同移动量处的2D 互相关值（图c），搜索最大互相关值对应的水平和垂直校正量，并对待校正道集进行时空变换和重采样（图d）．

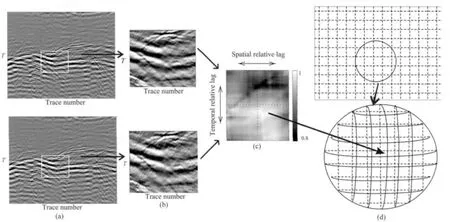
图2 地震图像校准示意图［16，22］（a）待校正道集（上）模型道集（下）；（b）计算2D互相关提取的局部窗口数据；（c）计算的2D互相关（横轴：空间相对移动量 纵轴：时间相对移动量），互相关最大值对应的移动量为所要估计的水平和垂直校正量；（d）在整个道集上逐点估计2D校正量，并对待校正道集进行时空变换和重采样．Fig．2 The diagram of seismic image warping［16，22］（a）The gather to be corrected（top）and the model gather（bottom）；（b）The extracted local window data used for 2Dcross－correlation computation；（c）The computed 2Dcross－correlation（lateral axis：spatial relative lag，vertical axis：temporal relative lag）．The lateral and vertical corrected values correspond to the maximum cross－correlation；（d）The corrected values are computed point by point in the whole gather．Then the gather to be corrected is transformed in the space and time domain and resampled．

图像校准分为校正量估计和重采样两部分．本文方法首先对COG 道集逐点计算水平和垂直校正量，并估计成像点位置，然后对COG 道集重采样估计成像点振幅．

2．1 水平和垂直校正量计算

在本文方法中，为消除不同时间和空间相对移动量时窗口能量差异对互相关计算的影响，度量两个道集的相似性时采用2D 归一化互相关［28］：

C（r，s，l1，l2）代表待校正道集g和模板道集f之间的2D 归一化互相关值，d0（r，s，l1，l2）代表待校正道集g和模板道集f之间的2D 互相关值，d1（r，s，l1，l2）代表模板道集f的自相关值，d2（r，s，l1，l2）代表待校正道集g的自相关值，l1，l2表示时间和空间相对移动量，［－p，p］、［－q，q］分别表示时间和空间相对移动量的范围，［－w，w］、［－v，v］分别表示归一化互相关窗口的时间和空间范围．

为计算2D 局部归一化互相关值，在道集f中包含点（r，s）开一个窗口f（t1，x1），其中t1＝（r－w，…，r－1，r，r＋1，…，r＋w），x1＝（s－v，…，s－1，s，s＋1，…，s＋v），在道集g中包含点（r，s）开一个窗口g（t2，x2），其中，t2＝（r－w，…，r－1，r，r＋1，…，r＋w），x2＝（s－v，…，s－1，s，s＋1，…，s＋v）．起初选择t1＝t2、x1＝x2，然后以不同的2D 相对移动量l＝（l1，l2）改变（t2，x2），计算在该相对移动量时的局部归一化互相关值C（r，s，l1，l2）．整个计算过程如图3所示．窗口的选择根据地震子波长度和待校正道集上的同相轴倾角决定［17］．

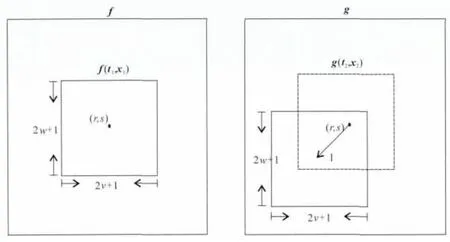
图3 2D 局部互相关计算示意图［17］Fig．3 The diagram of 2Dlocal cross－correlation computation［17］

传统方法在道集的稀疏点上按图3所示计算局部归一化互相关值，并通过搜索最大互相关来估计校正量，然后进行插值计算其它点的校正量［29］．虽然这种方法提高了计算效率，但降低了道集上其它各点校正量估计的精度．为了均衡互相关和校正量计算的精度和效率，首先计算待校正道集g在相对移动量l＝（l1，l2）时，与模板道集f在每一个点的乘积，然后对乘积结果进行快速均值滤波［30－31］以计算局部互相关值d0（r，s，l1，l2）：

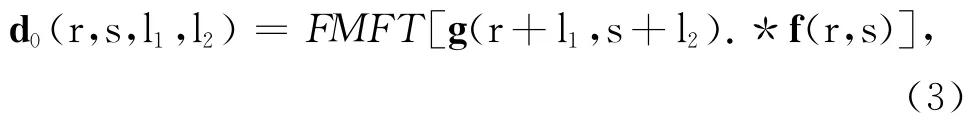
其中，FMFT 表示快速均值滤波，时间和空间窗口大小分别为2＊w＋1，2＊v＋1，．＊ 表示点乘运算．同理：

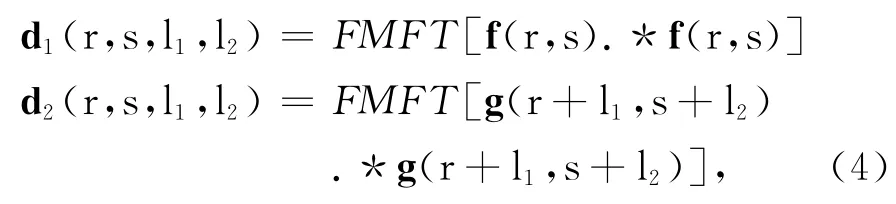
最后采用公式（2）计算每一点的归一化互相关值C（r，s，l1，l2）．整个计算过程如图4所示．这种归一化互相关计算方法简单易行，并能够避免在对相邻位置点计算局部互相关时，产生的重复相乘和相加运算．重复该过程计算在其它相对移动量的局部归一化互相关值．对各个待校正道集g计算互相关时采用相同的模板道集f，因此道集f的自相关值首先计算并进行保存，以进一步降低各道集归一化互相关的总体计算量．传统方法［2－4］在垂直方向计算1D归一化互相关值，因此本文方法在归一化互相关的计算量大约是传统方法的（2q＋1）（2v＋1）倍．

图4 2D 归一化互相关计算示意图Fig．4 Illustration for computing the 2Dnormalized cross correlation

在计算不同2D 移动量对应的局部互相关值后，遍历搜索局部互相关的最大值，对应的校正量位于整数采样点处．然而，即使小于整数采样点的校正量会产生足够大的地震同相轴扰动［22］．为避免地震数据的离散采样特性，可以假设在不同整数相对移动量时的互相关值满足一个连续凸函数［32－34］．在此基础上求解互相关函数的最大值来估计非整数的校正量．

Newton－Raphson方法［16，24］已经被用来估计最大互相关值对应的非整数校正量．我们采用求导方法来估计采样点（r，s）处最大互相关对应的校正量，式（2）定义的2D 归一化互相关函数在最大值附近区域内可近似满足如下的二元抛物面函数［32－34］：

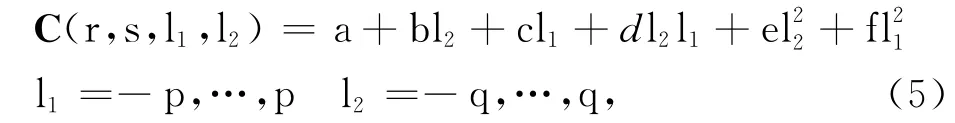
计算得到整数相对移动量（l1，l2）下的归一化互相关后，未知参数向量（a，b，c，d，e，f）可以利用多项式拟合方法进行估计．令归一化互相关函数C（r，s，l1，l2）的一阶导数为零，可以得到采样点（r，s）处最大互相关对应的时间校正量dt和空间校正量dx如下式：

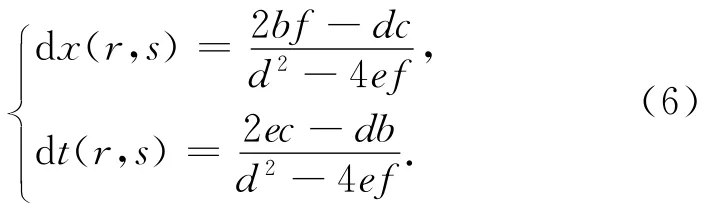
图5a给出了校正量估计的示意图，计算各个整数移动量对应的互相关，搜索所计算互相关最大值对应的整数移动量（左图），并取其周围的整数移动量及其互相关值对多项式进行拟合（中图），然后利用求导方法估计非整数校正量（右图），叉号表示所估计的校正量位置．

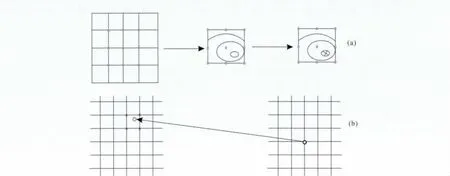
图5 成像点位置和振幅计算示意图［16，24］（a）不同移动量下的归一化互相关值（左图），用于拟合多项式的互相关值（中图），叉号为求导方法估计的校正量位置（右图）；（b）校正前成像点位置（左图）和校正后成像点位置（右图）．Fig．5 The diagram of estimating image point position and amplitude（a）The normalized cross－correlation of different relative lags（left）．The normalized cross－correlation chosen for polynomial fitting（middle）．The cross corresponds to the corrected values position by the derivation method（right）；（b）The image point position before correction（left）and after correction（right）．

地震数据的局部连续性决定了所估计的水平和垂直校正量也是局部连续的［16］．而地震道集中的噪声会影响校正量计算的准确性，校正量估计的野值或奇异值会导致输出的校正道集产生不合理的突变或不连续现象［16］．沿主要地质构造特征移动的校正量会计算得到大的互相关值，因此各点的最大互相关值可用来衡量该点处所估计校正量的相对重要性［16］．本文对所估计的水平校正量和垂直校正量分别进行加权均值滤波处理，加权系数选择为各点所对应的最大互相关值．而且，最大互相关对应的时间和空间位置不能偏离原始成像点位置太远，因此采用简单的阈值处理将所估计的时间校正量和空间校正量限制在时间相对移动量［－p，p］和空间相对移动量［－q，q］的范围之内．

上述所计算的校正量表征待校正道集和输出道集的映射关系．基于这种时间—空间映射关系所估计的成像点位置在大部分情况下位于非整数位点．因此，需要在亚像素域对待校正道集进行重采样．

2．2 基于双线性内插的重采样

为同时消除2D 叠前偏移COG 道集的水平和垂直校正量，应该对抽取的每一个COG 道集逐点进行图像校准．利用式（1）表示的输入和输出道集的映射关系，对待校正道集上的每一点估计正确的成像点位置，其中dt、dx为求导方法计算的时间和空间方向的校正量．图5b为对COG 道集上某点进行校正量消除，并估计正确成像点位置的示意图．图5b右图中白点表示输出道集中的成像点位置，图5b左图中白点表示该成像点在待校正道集的位置．

由图1和图5b可知，地震数据的离散采样特性决定了所估计的成像点位置位于亚像素域．Wolberg利用多种内插算子对待校准图像进行重采样［18］．在确定亚像素位置周围最近的四个离散采样点后，如图5b左图中的黑点位置，本文采用双线性内插方法对所估计各点的成像振幅进行重建．局部的内插算子能够尽量减小对地震数据中断层等非连续性的模糊效应，并能提高重采样的计算效率［16］．

2．3 算法流程图

综上所述，对叠前地震道集（如偏移后的CIG道集或动校正后的CMP 道集）进行水平和垂直校正量消除的算法流程图如图6．

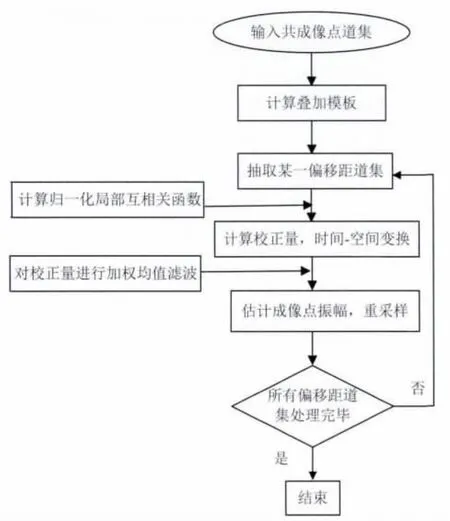
图6 基于地震图像校准的水平和垂直校正量消除算法流程图Fig．6 The diagram of removing lateral and verical corrected values based on seismic image warping

本文方法计算不同时间和空间相对移动量下的2D 归一化互相关，并估计互相关最大值对应的时间和空间校正量．传统方法计算时间相对移动量下的1D 互相关最大值来估计时间校正量，当将本文方法表征2D 局部归一化互相关的空间窗口范围v设为0，空间相对移动量的范围q设为0，即可得到传统方法［2－4］消除垂直校正量的处理结果．

3 应用实例

为验证本文方法的有效性，对存在水平和垂直校正量的人工模拟数据和实际数据进行处理，测试该方法消除水平和垂直校正量的效果，并与传统方法［2－4］进行垂直校正量消除的结果进行对比．在该应用实例中，［－p，p］、［－q，q］分别表示时间和空间相对移动量的范围，［－w，w］、［－v，v］分别表示归一化互相关窗口的时间和空间范围，m、n分别表示对整个道集估计的水平和垂直校正量进行加权均值滤波的时间和空间大小．

3．1 合成数据

首先人工合成CIG 道集进行测试．选取一个叠加剖面，采样间隔0．002s，道间距12．5m，图7a所示的叠加剖面有1000道，每道有1000个采样点，对黑色框图内各点随机施加水平和垂直扰动量并进行重采样后的结果如图7b所示，图8a为各点包含的水平校正量，在－4道到4道范围内随机选取，图8c为垂直校正量，在－4个采样点到4个采样点范围内随机选取．图7c和图7d为图7a和图7b上面白色方框的放大结果，图7e和图7f为图7a和图7b下面白色方框的放大结果，对比图7c和图7d、图7e和7f箭头位置可发现有明显的水平和垂直校正量存在．对同样区域随机施加水平和垂直扰动量模拟生成50个COG 道集，抽取第500个CIG 道集如图9b所示，对比图9a未施加校正量的CIG 道集，可知水平和垂直校正量的存在使CIG 道集同相轴的一致性变差．

采用图像校准的方法，p＝4 采样点，q＝4 道，w＝2采样点，v＝2道，m＝5采样点，n＝5道，同时消除水平和垂直校正量．图8b和图8d为对图7b的COG 道集所估计的水平和垂直校正量，逐个COG道集处理后的第500 个CIG 道集如图9c所示．同时对比传统方法消除垂直校正量的效果，p＝4采样点，q＝0道，w＝2采样点，v＝0道，m＝5 采样点，n＝5道，图8e为对图7b所估计的垂直校正量，不估计水平校正量．对比图8c、图8d和图8e框图可知，本文方法在估计水平校正量的同时，所估计的垂直校正量更准确．图9d为消除垂直校正量后抽取的第500个CIG 道集．对比图9c和图9d箭头位置表明本文算法能有效地同时消除水平和垂直校正量．

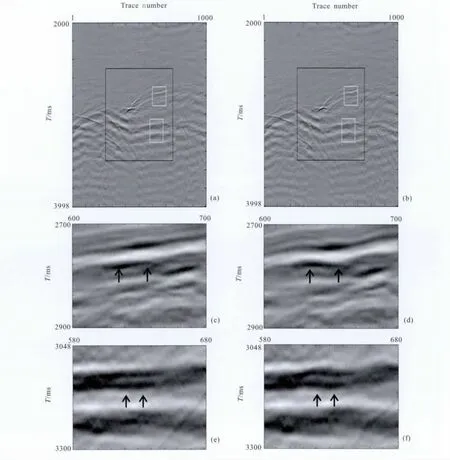
图7 模拟的COG 道集（a）黑色框图中不包含水平和垂直校正量的COG 道集；（b）黑色框图中包含水平和垂直校正量的COG 道集；（c）图（a）上面白色方框的放大结果；（d）图（b）上面白色方框的放大结果；（e）图（a）下面白色方框的放大结果；（f）图（b）下面白色方框的放大结果．Fig．7 The simulated COG gathers（a）The COG gather without lateral and vertical corrected values in the black rectangle；（b）The gather with lateral and vertical corrected values in the black rectangle；（c）The zoomed area of upper white rectangle in Fig．（a）；（d）The zoomed area of upper white rectangle in Fig．（b）；（e）The zoomed area of lower white rectangle in Fig．（a）；（f）The zoomed area of lower white rectangle in Fig．（b）．

图9 模拟的CIG 道集（a）不包含水平和垂直校正量的CIG 道集；（b）包含水平和垂直校正量的CIG 道集；（c）同时消除水平和垂直校正量的CIG 道集；（d）只消除垂直校正量的CIG 道集．Fig．9 The simulated CIGs（a）The CIG without lateral and vertical corrected values；（b）The CIG with lateral and vertical corrected values；（c）The CIG after eliminating the lateral and vertical corrected values simultaneously；（d）The CIG after removing the vertical corrected values only．

3．2 实际数据

将本文方法应用到实际数据处理中．该数据包含叠前时间偏移生成的1120个CIG 道集，生成该CIG 道集前已经进行了多次波消除，每个道集包含61道，道间距50m，每道2501个采样点，采样间隔2ms．图10a为前50个偏移距道集叠加生成的模板道集，图10b为第10个偏移距道集，只显示250到750道，200到3000ms的剖面，图10c和图10d分别为图10a和图10b框图的放大显示，对比箭头可知该偏移距道集相对模板道集存在水平和垂直校正量．

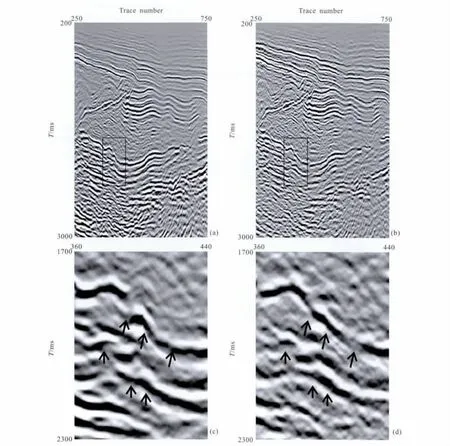
图10 叠加模板道集和第10个COG 道集（a）模板道集；（b）第10个COG 道集；（c）图（a）黑色框图的放大显示；（d）图（b）黑色框图的放大显示．Fig．10 The stack model gather and the tenth COG（a）The model gather；（b）The tenth COG；（c）The zoomed area of the black rectangle in Fig．（a）；（d）The zoomed area of the black rectangle in Fig．（b）．

选择处理参数，p＝3 采样点，q＝2 道，w＝30采样点，v＝2道，m＝5采样点，n＝5道，同时消除水平和垂直校正量．图11（a，b）为对第10个COG道集同时进行水平和垂直校正量消除，所估计的水平校正量和垂直校正量．对比传统方法进行垂直校正量消除的效果，选择处理参数，p＝3采样点，q＝0道，w＝30采样点，v＝0道，m＝5采样点，n＝5道．图11c为传统方法对第10个COG 道集所估计的垂直校正量，不进行水平校正量估计．下面从CIG 道集和叠加剖面上，将本文方法同时进行水平和垂直校正量消除的效果和传统方法进行垂直校正量消除的效果进行对比．

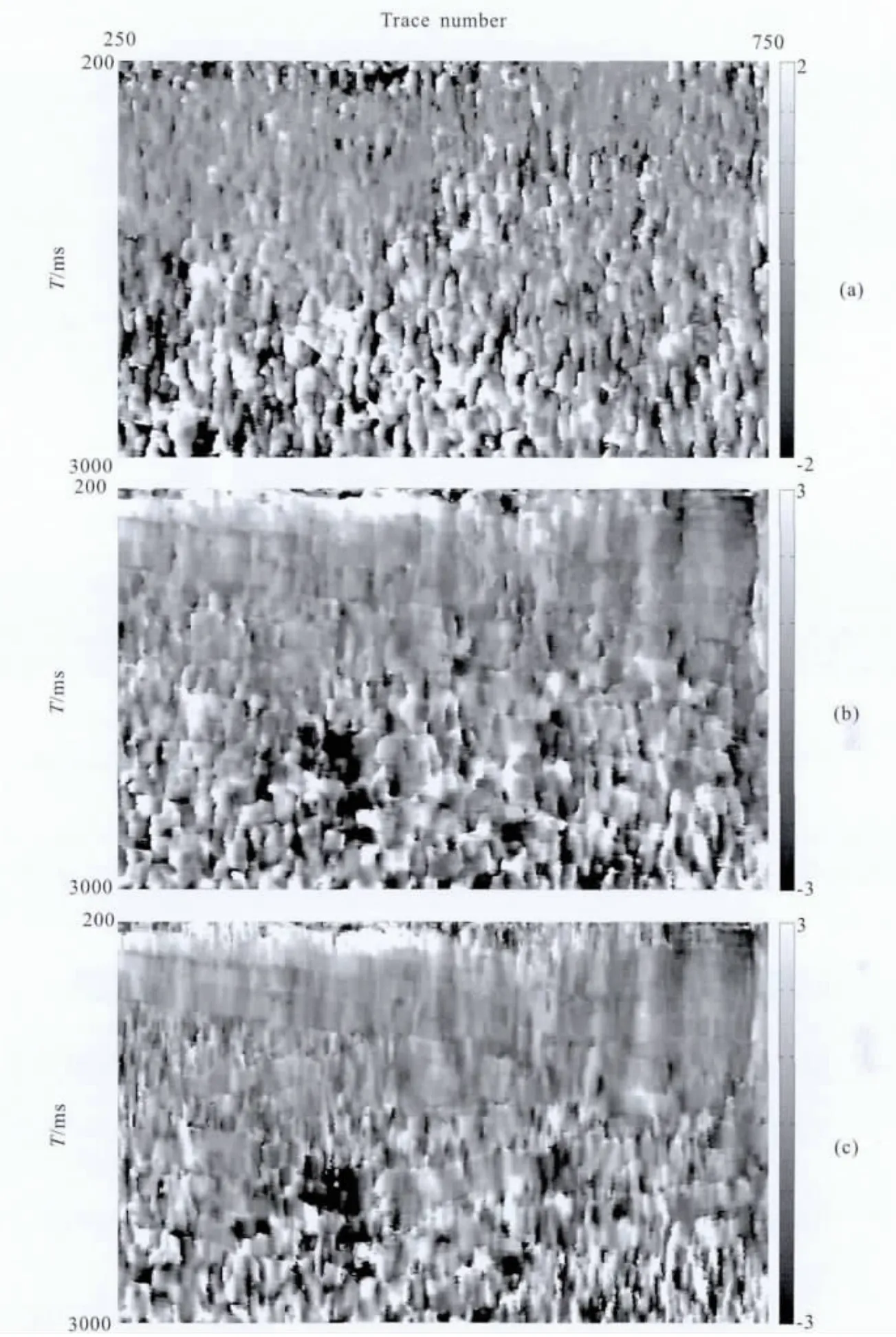
图11 第10个COG 道集估计的校正量（a）本文方法估计的水平校正量；（b）本文方法估计的垂直校正量；（c）传统方法估计的垂直校正量．Fig．11 The estimated corrected values of the tenth COG（a）The estimated lateral corrected values by the method in this paper；（b）The estimated vertical corrected values by the method in this paper；（c）The estimated vertical corrected values by the traditional method．

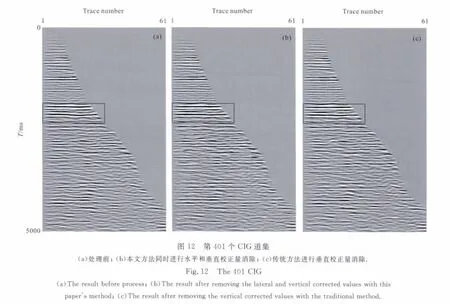
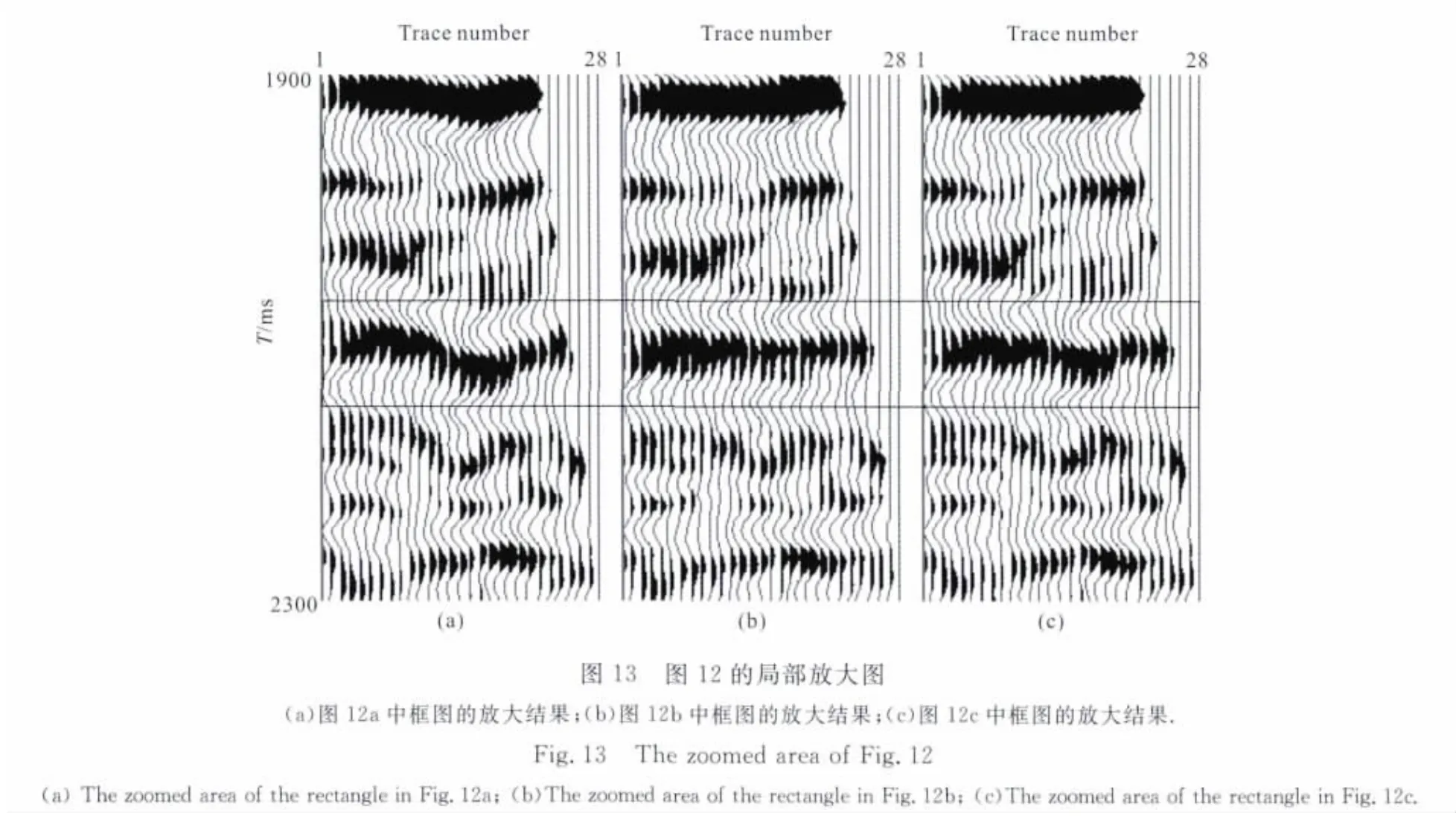
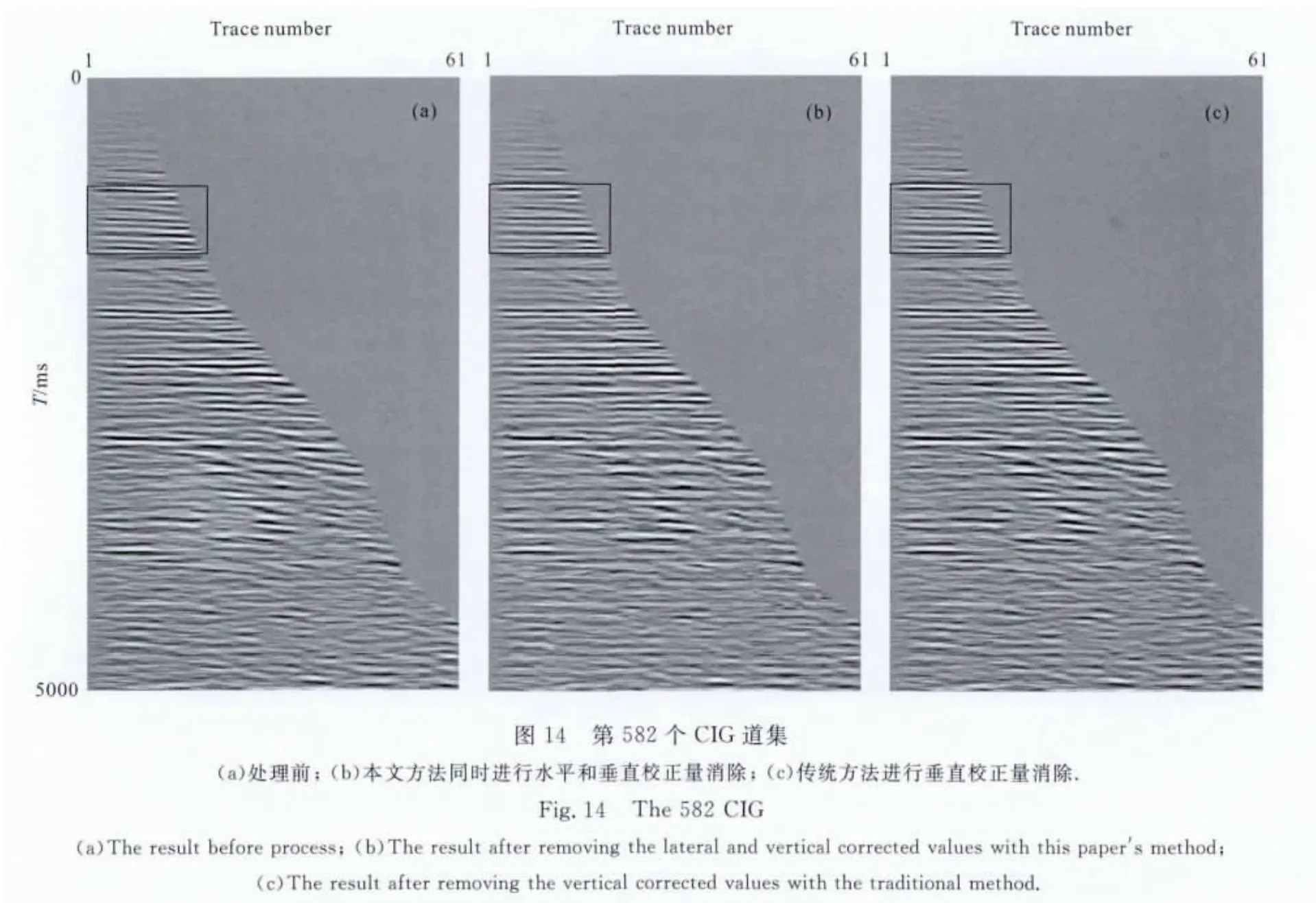
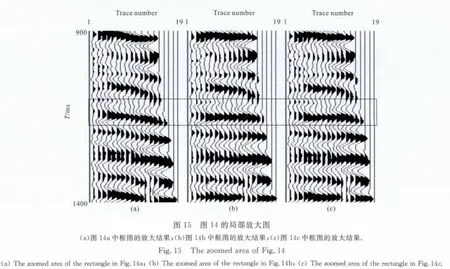
图12a为处理前第401个CIG 道集，图12b为对401个CIG 道集同时进行水平和垂直校正量消除的结果，为对比显示处理效果，将图12（a、b）方框内的区域进行放大，图13（a，b）分别对应图12（a，b）中框图的放大结果．图14（a，b）分别为第582 个CIG 道集处理前后的结果，图15（a，b）分别为图14（a，b）中框图的放大结果．对比图13（a，b）、图15（a，b）框图内的同相轴可知，经过处理后的成像点道集中同相轴的一致性增强．

图12c为传统方法对第401 个CIG 道集进行垂直校正量消除的结果，图13c为图12c中框图的放大结果；图14c为传统方法在第582个CIG 道集的处理结果，图15c为图14c中框图的放大结果．对比图13b和图13c、图15b和图15c框图内的同相轴可知，同时进行水平和垂直校正量消除，能得到同相轴一致性更好的CIG 道集．

下面在叠加剖面上对比校正量消除的效果．图16a为处理前的叠加道集，图16b为本文方法同时进行水平和垂直校正量消除的叠加剖面，其中只显示出250到750道，200 ms到3000 ms的剖面，将其中的部分区域进行放大，图17（a，b）分别给出了图16（a，b）右边框图的放大结果，图17（d，e）为图16（a，b）左边框图的放大结果．黑色箭头表明经水平和垂直校正量消除后叠加剖面的同相轴变清晰，连续性变强．图16左边竖线表示第401个CIG道集的叠加道位置，右边竖线表示第582个CIG 道集的叠加道位置，图12—15已经给出了第401个和582个CIG 道集的处理前后结果，经过水平和垂直校正量消除后的CIG 道集同相轴的扰动减小，同相轴的一致性增强，这样所得到的叠加结果的分辨率更高，有利于进一步的地震反演和解释．

图16c为传统方法进行垂直校正量消除的叠加结果，图17（c，f）分别为图16c右边框图和左边框图的放大结果．将图17（b，c，e，f）中的框图部分放大，分别显示在图18（a，b，c，d）．图18（a，b）和图18（c，d）中的黑色箭头表明，同时进行水平和垂直校正量消除后，叠加结果的同相轴更加清晰连续，分辨率更高，进一步验证了本文算法同时消除水平和垂直校正量的有效性．

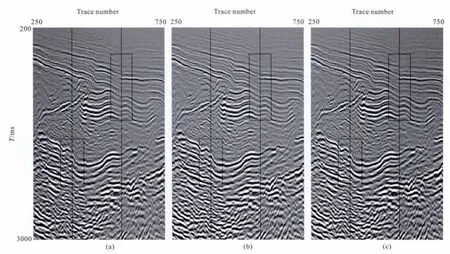
图16 叠加剖面（a）处理前；（b）本文方法同时进行水平和垂直校正量消除；（c）传统方法进行垂直校正量消除．Fig．16 The stack profile（a）The result before process；（b）The result after removing the lateral and vertical corrected values with this paper′s method；（c）The result after removing the vertical corrected values with the traditional method．

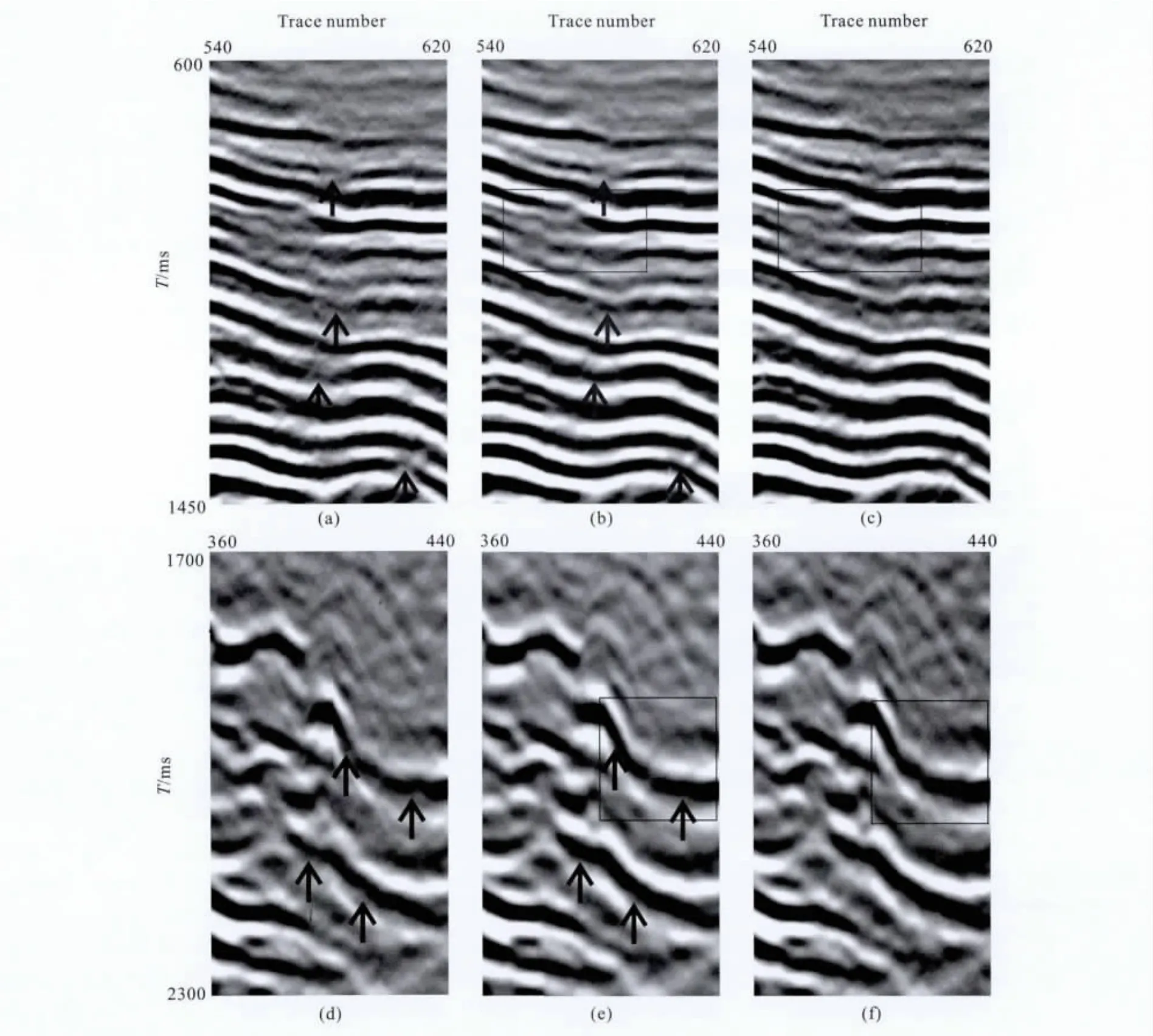
图17 图16的局部放大图（a）图16a右边框图放大结果；（b）图16b右边框图放大结果；（c）图16c右边框图放大结果；（d）图16a左边框图放大结果；（e）图16b左边框图放大结果；（f）图16c左边框图放大结果．Fig．17 The zoomed area of the Fig．16（a）The zoomed area of the right rectangle in Fig．16a；（b）The zoomed area of the right rectangle in Fig．16b；（c）The zoomed area of the right rectangle in Fig．16c；（d）The zoomed area of the left rectangle in Fig．16a；（e）The zoomed area of the left rectangle in Fig．16b；（f）The zoomed area of the left rectangle in Fig．16c．

图18 图17框图的局部放大图（a）图17b框图放大结果；（b）图17c框图放大结果；（c）图17e框图放大结果；（d）图17f框图放大结果．Fig．18 The zoomed area of the Fig．17（a）The zoomed area of the rectangle in Fig．17b；（b）The zoomed area of the rectangle in Fig．17c；（c）The zoomed area of the rectangle in Fig．17e；（d）The zoomed area of the rectangle in Fig．17f．

在本文方法中时间和空间相对移动量范围过大，易导致所估计的成像点位置偏离真实位置，校准后产生串层现象；时间和空间相对移动量范围过小，会导致较大校正量的估计误差．过大的互相关时间和空间窗口导致校正量估计的分辨率降低，窗口过小，互相关计算易受噪声影响．同样对所估计水平和垂直校正量进行加权均值滤波的参数应试验选取，在滤除噪声和野值影响的同时，尽量保持所估计校正量的局部细节．

4 结 论

基于地震图像校准的水平和垂直校正量消除方法应用在经过动校正的CMP道集或叠前偏移后的CIG 道集，处理之前需要进行多次波消除．本文方法以叠加剖面为模板，逐个COG 道集消除水平和垂直校正量．以不同的水平和垂直相对移动量计算2D归一化互相关函数，采用求导方法估计非整数校正量，并在亚像素域估计正确的成像点振幅．模型数据和实际数据的处理结果表明本文方法可以同时消除水平和垂直方向上的校正量，增强CIG 道集中同相轴的一致性，提高叠加剖面的分辨率．

本文方法在COG 道集上逐点计算2D 归一化互相关函数并估计校正量，可以提高整个道集上校正量消除的准确性，计算量主要集中在互相关计算和校正量估计上．为均衡计算效率和计算精度，本文采用先点乘再进行快速均值滤波的方法，来计算待匹配道集和模板道集的自相关和互相关，最后计算2D 归一化互相关．2D 互相关计算的窗口大小需要通过根据地震子波长度和同相轴的倾角试验获得．对所估计的校正量进行2D加权均值滤波能有效消除计算误差影响，提高成像点位置和振幅估计的准确性．

（References）

［1］ 夏洪瑞，陈德刚，周开明．剩余动校正量的拾取与消除．石油地球物理勘探，1997，32（6）：872－877．

Xia H R，Chen D G，Zhou K M．Pickup and removal of residual normal moveout．OilGeophysicalProspecting（in Chinese），1997，32（6）：872－877．

［2］ Hinkley D，Bear G W，Dawson C．Prestack gather flattening for AVO．74th Annual International Meeting， SEG，Expanded Abstracts，2004：271－273．

［3］ Duveneck E，Traub B．Automatic moveout correction by local event correlations on coherency－enhanced gathers．76th Annual International Meeting，SEG，Expanded Abstracts，2006：3036－3040．

［4］ Gulunay N，Gamar F，Hoeber H，et al．Robust residual gather flattening．77th Annual International Meeting，SEG，Expanded Abstracts，2007：229－233．

［5］ 慎国强，王玉梅，孟宪军等．基于时频分析的地震道集校平技术应用．中国石油大学学报（自然科学版），2010，34（1）：34－36，45．

Shen G Q，Wang Y M，Meng X J，et al．Application of seismic gather flattening technique based on time－frequency analysis．JournalofChinaUniversityofPetroleum（Editionof NaturalScience）（in Chinese），2010，34（1）：34－36，45．

［6］ Lu W K，Liu J．Estimation and removal of the residual normal moveout based on the S－transform．Congress on Image and Signal Processing，2008：573－576．

［7］ Gulunay N，Magesan M，Roende H．Gather flattening based on event tracking for each time sample．70th EAGE Conference and Exhibition，2008．

［8］ Gulunay N，Magesan M，Roende H．Gather flattening．The LeadingEdge，2007，26（12）：1538－1543．

［9］ Gulunay N．Polarity blind and polarity sensitive gather flattening methods．74th EAGE Conference and Exhibition，2012．

［10］ 林伯香，孙建国．相位替换法剩余时差校正．石油物探，2001，40（3）：15－22．

Lin B X，Sun J G．Residual moveout correction by using phase replacement．GeophysicalProspectingforPetroleum（in Chinese），2001，40（3）：15－22．

［11］ 王开燕，李慧，官波等．相位剩余时差校正方法在提高分辨率中的应用．大庆石油学院学报，2007，31（6）：14－17．

Wang K Y，Li H，Guan B，et al．Application of residual moveout correction to the improvement of resolution．JournalofDaqingPetroleumInstitute（in Chinese），2007，31（6）：14－17．

［12］ 王云专，杨立伟，李素华．剩余时差校正及泊松比反演．地球物理学进展，2006，21（1）：214－218．

Wang Y Z，Yang L W，Li S H．Residual moveout correction and Poisson′s ratio inversion．Progressin Geophysics（in Chinese），2006，21（1）：214－218．

［13］ Lichman E．Automated phase－based moveout correction．69th Annual International Meeting，SEG，Expanded Abstracts，1999：1150－1153．

［14］ Liu G C，Fomel S，Jin L，et al．Stacking seismic data using local correlation．Geophysics，2009，74（3）：V43－V48．

［15］ Liu G C，Fomel S，Chen X H．Stacking angle－domain common－image gathers for normalization of illumination．GeophysicalProspecting，2011，59（2）：244－255．

［16］ Perez G，Marfurt K J．Warping prestack imaged data to improve stack quality and resolution．Geophysics，2008，73（2）：P1－P7．

［17］ Wolberg G．Digital image warping．IEEE Computer Society Press，1990．

［18］ Lee S Y，Chwa K Y，Hahn J，et al．Image morphing using deformation techniques．JournalofVisualizationandComputer Animation，1996，7（1）：3－23．

［19］ 郑亚琴，田心．医学图像配准技术研究进展．国际生物医学工程杂志，2006，29（2）：88－92．

Zheng Y Q， Tian X． Development of medical image registration．InternationalJournalofBiomedicalEngineering（in Chinese），2006，29（2）：88－92．

［20］ Nickel M，Sonneland L．Non－rigid matching of migrated timelapse seismic．69th Annual International Meeting，SEG，Expanded Abstracts，1999：872－875．

［21］ Rickett J E，Lumley D E．Cross－equalization data processing for time－lapse seismic reservoir monitoring：A case study from the Gulf of Mexico．Geophysics，2001，66（4）：1015－1205．

［22］ Hall S A，MacBeth C，Barkved O I，et al．Cross－matching with interpreted warping of 3D streamer and 3D oceanbottom－cable data at Valhall for time－lapse assessment．GeophysicalProspecting，2005，53（2）：283－297．

［23］ Hall S A．A methodology for 7D warping and deformation monitoring using time－lapse seismic data．Geophysics，2006，71（4）：O21－O31．

［24］ 郭念民，吴国忱．非重复采集时移地震正演模拟及可行性分析．地球物理学进展，2012，27（1）：232－245．

Guo N M，Wu G C．Forward－modeling and feasibility study of non－repeating acquired time－lapse seismic exploration．ProgressinGeophys．（in Chinese），2012，27（1）：232－245．

［25］ 赵伟．中国海上时移地震技术应用的可行性研究．勘探地球物理进展，2003，26（1）：30－34．

Zhao W．Feasibility study on time－lapse seismic offshore China．ProgressinExplorationGeophysics（in Chinese），2003，26（1）：30－34．

［26］ Grubb H，Tura A，Hanitzsch C．Estimating and interpreting velocity uncertainty in migrated images and AVO attributes．Geophysics，2001，66（4）：1208－1216．

［27］ 李振春，张军华．地震数据处理方法．东营：中国石油大学出版社，2006．

Li Z C，Zhang J H．The Method of Seismic Data Processing．Dongying：China University of Petroleum Press，2006．

［28］ Barnea D I，Silverman H F．A class of algorithms for fast digital image registration．IEEETrans．Computers，1972，21（2）：179－186．

［29］ Perez G，Marfurt K J．Fine－tuning your seismic image：prestack data warping to improve stack quality and resolution．76th Annual International Meeting，SEG，Expanded Abstracts，2006：2475－2479．

［30］ Pan J J，Tang Y Y，Pan B C．The algorithm of fast mean filtering．WaveletAnalysisandPatternRecognitionConference，2007：244－248．

［31］ Rakshit S，Ghosh A，Shankar B U．Fast mean filtering technique（FMFT）．PatternRecognition，2007，40（3）：890－897．

［32］ Steger C．An unbiased detector of curvilinear structures．IEEETransactionsonPatternAnalysisandMachineIntelligence，1998，20（2）：113－125．

［33］ Steger C．Unbiased extraction of curvilinear structures from 2Dand 3Dimages ［Ph．D．thesis］．München：Technical University of München，1998．

［34］ 雷鸣，张广军．基于互相关的图像匹配亚像素定位．光电工程，2008，35（5）：108－113．

Lei M，Zhang G J．Image orientation algorithm with subpixel accuracy based on correlative matching method．Opto－ElectronicEngineering（in Chinese），2008，35（5）：108－113．