薄互层地震成像中高分辨率处理方法

刘志伟，王彦春，赵会欣，刘学清

1 中国地质大学（北京）地球物理与信息技术学院，北京 100083

2 教育部地球探测重点实验室，北京 100083

3 中国石油集团东方地球物理公司，河北涿州 072751

1 引 言

薄互层指不同岩性薄层间隔出现的一种地质体．相邻层地震波速度不同，以致地震记录中薄互层单层顶、底反射系数符号相异、走时差小等特点；由于激发子波频带有限，薄互层有效反射波呈现为子波相互叠加、相互干涉的结果［1－2］．纵向上，这种干涉叠加削弱薄互层界面的真实反射系数，使地震记录成为一组整体地震响应［3－4］．横向上，薄互层砂泥岩岩性突变位置构成尖灭，甚至出现正交的“泥岩墙”特例．根据惠更斯绕射叠加原理，砂泥岩突变位置两侧速度不同造成两侧绕射振幅叠加不能相互消弱，使地震强反射轴断续出现或者存在相位差［5］．因此，薄互层成像既要考虑纵向分辨率又要兼顾横向分辨率，其处理方法选择和应用对提高成像分辨率至关重要．

地震纵向分辨率起源于光学点绕射的研究，Rayleigh（1945）通过两个相同反射系数和零相位子波定义其极限为1/4 波长［6］；在相同子波条件下，Ricker（1953）将两个子波混叠后取波形的二阶导数极值点间距离（小于1/4波长），将其定义为纵向分辨率极限［7］；Widess（1973）基于两个相异极性反射系数和零相位子波，通过时间一阶导数定义纵向分辨率极限为1/8 波长［8］；Schoenberger（1974）讨 论了零相位和最小相位子波的分辨率极限问题，提出在相同振幅谱条件下，零相位子波的分辨率高于最小相位子波的分辨率［9］．以上作者从地震子波角度详细讨论了定义纵向分辨率极限和提高纵向分辨率的理论基础，可见提高薄互层纵向分辨率的关键是解决地震子波压缩问题．Kallweit和Wood（1982）基于相同反射系数和反向反射系数楔状模型，应用连续曲线方式揭示调谐振幅和地层厚度间的变化规律［10］；Voogd和Rooijen（1983）给出有限带宽子波和不同频带镶边条件下的纵向分辨率讨论，认为在相同频宽条件下，频带镶边越陡，分辨率就越低［11］；Robertson（1984）基于楔状模型和Ricker子波，从瞬时地震属性角度研究地震纵向分辨率，认为地震瞬时属性可以提高地震纵向分辨能力［12］；Juhlin（1993）和Liu（2003）讨论1/8波长薄层与AVO 的关系［13－14］；从分辨率研究最新发展趋势来看，薄互层纵向分辨率提高除了合理压缩地震子波外，还要考虑薄互层振幅问题．Sheriff在地球物理百科辞典中借用物理光学定义，给出地震菲涅尔带的地震横向分辨率定义；Berkhout（1984）基于空间子波概念讨论横向分辨率问题，认为地震数据波数谱与横向分辨率有一定关系［15］；Safar（1985）基于Kirchhoff理论论述空间绕射点间横向分辨率问题，提出影响横向分辨率的因素有：偏移孔径、空间采样间隔、速度误差和地震数据主频［16］；Knapp（1990）基于有限频带数据讨论菲涅尔带性质，揭示了不同菲涅尔带的时频变化关系［17］；Chen（1999）在总结前人的基础上，提出横向分辨率及其动态范围的概念，并给出计算公式［18］．

从以上研究可以看出，影响地震纵、横向分辨率的主要因素可归结为：地震子波主频、频带和偏移算子．目前常规反褶积和PSTM 技术对于子波频率在不同处理阶段的变化没有给予足够的关注，尤其对薄互层的高分辨成像还存在不足．本文认为，薄互层成像应该以保幅的、岩性处理方法为基础，综合考虑叠前时间偏移前、偏移过程中、偏移后三个过程的子波频率变化，分阶段地采取不同的高分辨处理方法补偿和保护地震子波高频信息，提高薄互层成像精度．为此，本文通过研究，提出了叠前时间偏移前采用子波高频补偿、叠前时间偏移中采用子波频率保护、叠前时间偏移后采用子波频率一致性拓展的联合处理方法，对薄互层进行成像，数值计算和实际资料处理都证明了这一联合方法的有效性．

2 理论方法

2．1 叠前时间偏移前反Q 滤波补偿高频衰减

地震波在薄互层传播时，存在球面扩散和层间滤波效应；这种效应对高频成分有一定的衰减，导致地震记录在较晚时间分辨率较低、子波非稳态性（子波形状和带宽随时间而变化）增强［19－20］．针对这种高频衰减，目前地震资料处理广泛采用反褶积、谱白化、小波变换频率补偿等方法．反褶积作为常规方法，当地震子波非稳态性不可忽略时，Wiener线性滤波器设计必须对时间记录分时窗处理，而在时窗交叠位置分时窗反褶积处理对薄互层地震子波存在明显的破坏作用．谱白化直接处理信号的振幅谱，通过展平振幅谱来达到频率补偿目的，但当反射系数非白化时，无疑会破坏薄互层间反射系数的相对关系．此外，谱白化频率分解后的重构是非正交变换，难以达到相对保持振幅条件．基于小波变换的频率补偿方法将数据分解到不同尺度的时频域，由于在任意时间的小波函数和尺度函数都是正交的，所以对这些尺度函数做过分的处理都会破坏这种正交性，其结果同谱白化一样会破坏薄互层间反射系数序列．由此可见，反射系数白化和地震信号稳态性条件对薄互层高频信息补偿起到关键制约作用．

地震薄互层信号非稳态性主要来源于非弹性介质内部地球物理属性，减小非稳态性的方法主要是通过波前扩散补偿和频率衰减补偿处理［19］．波前扩散补偿可以采用反球面扩散补偿，而频率衰减与地层品质因子Q有关，可以通过反Q滤波方法补偿时间和空间频率差异［21］．地震波在地下层状或连续介质中传播时，要经受与频率有关的衰减及频散引起的相位畸变，单层振幅和相速度的频散关系为：

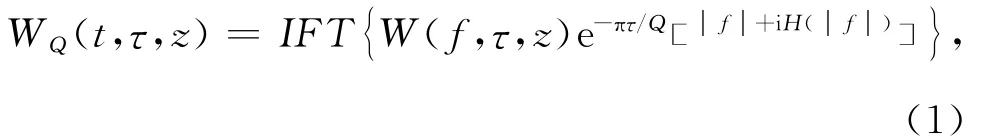
其中Q为品质因子，τ为传播时间，W（f，τ，z）为地震波在纯弹性介质传播的振幅谱，f为频率，H（·）是确保获得因果信号的Hilbert变换，IFT｛｝为傅氏反变换．假设Q为不随频率变化的常数，单层振幅和相速度的频散关系可表示为：

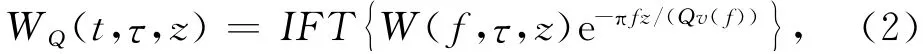
其中

fc为截止频率，在公式（2）中，薄层相速度取决于频率，这是因为地震波在吸收介质中传播必须要求是因果的．实际上，当假设Q与频率无关时，公式（1）与（2）等价，公式（3）用速度频散关系显式代替公式（1）的相位项．当频率等于抽样频率时，公式（1）与（2）等价．衰减强度既随着频率增加而增加，又随着薄层间传播路径的增加而增大，相速度也随着频率增加而增加，直到截止频率．由此，应用反Q滤波可以补偿薄互层对地震子波的高频衰减，增加地震信号的稳态性［22］．对于Q逆矩阵求解存在多种方法，目前较为稳定的方法是来自VSP资料的离散Q值和地震记录数据的扫描估算．为了验证薄互层高分辨率处理方法，设计如图1a的地球物理模型（总长1．44km，中间泥岩墙宽度40m，20m 道间距，每炮120道，主频35 Hz Ricker子波），通过各向同性声波方程正演单炮数据．提取泥岩墙附近单炮平均子波，计算相应频谱，如图1b所示，反Q滤波结果如图1c．可以看到，反Q滤波后单炮平均子波旁瓣得到压制、主瓣宽度减小，平均地震子波主频随之提高，相应单炮上薄互层之间和泥岩墙附近子波叠加和干涉效应减弱，纵向和横向分辨率得以提高，见图中绿色椭圆区域．

2．2 叠前时间偏移中子波频率保护

Kirchhoff叠前时间偏移基于波动方程Kirchhoff积分解，在薄互层成像方面，偏移算子响应明显优于FK 和有限差分偏移方法．通过图1a模型数据试验三种叠前偏移方法，NMO 叠加和PSTM 叠加结果及频谱如图2所示，注意到频谱图中20 Hz波峰可以理解为子波动校拉伸和叠加的低频效应；叠前偏移处理中试验FK、差分、Kirchhoff方法，图2b、2c、2d结果可以证明，基于射线理论的Kirchhoff叠前时间偏移对于薄互层成像表现出优势，尤其在高频保持方面，35Hz处最接近原始能量值0．003．但是，Kirchhoff叠前偏移技术仍存在偏移噪声和振幅保真等问题，这对薄互层成像来说尤为关键，直接影响薄互层横向分辨率［23］．不论是子波高频保持还是横向偏移归位，偏移对反射振幅和频率的影响主要来自加权因子，薄互层Kirchhoff叠前时间偏移必须对加权因子增加更多考虑．

图1 反Q 滤波高频补偿测试（a）深度模型及时间模型；（b）泥岩墙附近原始单炮、时窗1600～2500ms平均子波、子波频谱；（c）泥岩墙附近反Q 滤波后单炮、时窗1600～2500ms平均子波、子波频谱．Fig．1 Inverse Qfiltering analysis on a shot gather（a）Depth and time geophysical models；（b）A shot near mudstone wall，average wavelet in 1600～2500ms，spectrum of wavelet；（c）The filtered shot near mudstone wall，average wavelet in 1600～2500ms，spectrum of wavelet．

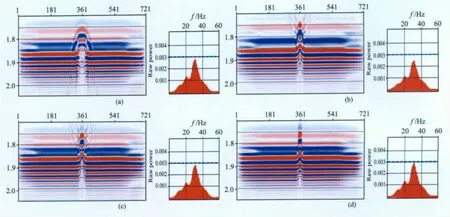
图2 薄层理论模型不同叠前偏移方法偏移成像对比（a）叠加剖面及频谱；（b）FK 偏移剖面及频谱；（c）有限差分偏移剖面及频谱；（d）Kirchhoff偏移剖面及频谱．Fig．2 Prestack migration methods analysis on thin interbeds model（a）NMO stack and spectrum；（b）FK migration stack and spectrum；（c）FD migration stack and spectrum；（d）Kirchhoff migration stack and spectrum．

考虑波动方程Kirchhoff积分解表达式：

其中，［P］为在延迟时τ＝t－r/v时刻波场P在区域A的积分．积分函数域中第一项依赖于波场的垂直变化，第二项称为近场源项，随1/r2衰减，这两项在偏移计算中往往被忽略；第三项称为远场项，构成Kirchhoff偏移的基础．在实际计算中，公式（4）离散化为：

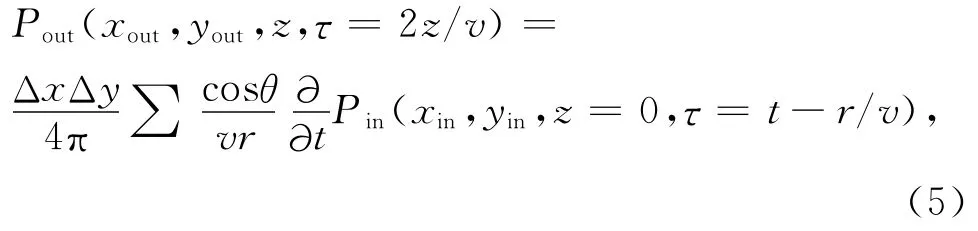
式中，Δx，Δy分别表示纵、横向的道间距，cosθ为倾角因子或者方向因子，1/vr为球面扩散因子，用来对绕射求和振幅和相位进行校正．公式（5）物理意义可以认为是从震源和接收点同时向成像点进行射线追踪或者波前计算，按照地震波走时从地震记录中拾取子波进行叠加，某些极大值点反映出反射体位置．然而，正是这个叠加过程对Kirchhoff叠前偏移有一定的降频作用，根本原因归于绕射叠加方法．理想情况下，面元内任意一点的成像值应该等于面元内不同偏移距轨迹上能量的叠加，成像点位于椭圆轨迹的公共切点上，能量最强，其它点却因为轨迹不同而被相互弱化；实际地震数据处理中，随着不同偏移距子波高频衰减，绕射叠加不能实现完全同相叠加，造成子波延续度增加、频带降低．

叠前偏移过程对子波频率的影响主要集中在加权因子上，加权因子具体包括波前扩散因子、倾斜因子或方向因子、子波整形因子［24］．根据惠更斯－菲涅尔原理，波前扩散因子是加在参与绕射叠加二次点源上的，表示子波从反射界面向外传播时振幅的衰减，然而地震数据在地面接收到的是经过波前扩散衰减后的振幅值，常规预处理中一般进行了球面扩散振幅补偿，所以，这个权因子在理论上没必要应用，或者说，在应用Kirchhoff叠前时间偏移之前应该反掉球面扩散补偿因子．倾斜因子是绕射曲线上振幅的加权因子，在绕射极小点值最大，两侧方向夹角余弦权系数逐渐减小，积分求和时绕射极小点对叠加结果贡献最大，可是，实践证明Kirchhoff偏移断面波成像中偏移孔径起到关键作用，这与倾斜因子的作用相矛盾，从成像角度说实现Kirchhoff叠前时间偏移应更注重偏移孔径的选择．整形因子是建立在地震记录中存在二次点源子波基础上，反射波成像和绕射波收敛通过叠加实现；对于给定子波而言，反射波与绕射波正半支在波形和相位上是同相的，而与绕射波负半支相位差180°，是否应用整形因子应该以地震井旁道与井曲线共同确定［25］．因此，薄互层Kirchhoff叠前时间偏移加权因子应该反掉预处理中的球面扩散补偿因子，注重偏移孔径选择，最后以地震井旁道确定是否加整形因子．

2．3 叠前时间偏移后子波频率一致性拓展

常规反褶积理论假设地震子波时不变和反射系数白噪，在最小平方准则下设计反滤波因子，基于其它目标函数判别准则的非线性反滤波器设计也对反射系数有一定的要求［26］，实践表明，高分辨单道脉冲反褶积不再适合相对振幅保持的薄互层岩性处理，保真保幅反褶积算法应是多道统计的．通过地表一致性反褶积（SCDC）和多道预测反褶积（ENSEMBLE PRDCON），基本使地震子波在纵、横向取得一致，能够在偏移成像前提高纵横向分辨率．叠前时间偏移在绕射收敛和偏移归位过程中，即使考虑最优加权Kirchhoff叠前时间偏移，一定程度上绕射叠加仍然对CRP道集产生了一定降频作用［27－28］；此外，预处理道集地震子波在时间与空间的不一致性在Kirchhoff叠前时间偏移中都会得到一定的混叠．因此，这两类子波变形或者不一致性对薄互层成像都将产生一定的影响．

因此，在叠前时间偏移后的CRP道集上进行子波一致性处理是必要的．经过反褶积预处理和叠前时间偏移，CRP道集各偏移距和各深度地震子波基本一致，应用单道预测反褶积进行子波一致性处理可以进一步拓展子波频带，提高分辨率［29］．常规的单道预测反褶积在子波最小相位的假设下，一般分时窗求取反褶积算子，如图3a所示，这对时窗边界产生一定的折衷处理，造成一定的不保幅性．子波调谐反褶积能够克服这方面的缺点，只要设计好统一的算子长度和预测距离，采用逐点计算反褶积算子的单道方式，进行零相位或最小相位算子设计，分析窗口从上至下依采样点进行子波估计和反褶积算子设计，如图3b所示．由于在单道上计算，反褶积算子在空间和时间有一定的差异，这种差异可以理解为预处理中地震子波不一致性的校正或者调谐［30］．

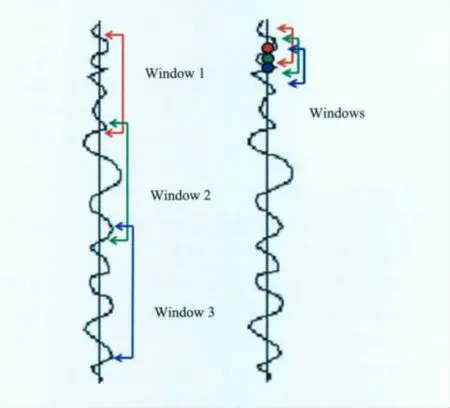
图3 常规反褶积与调谐反褶积时窗对比（a）常规反褶积时窗；（b）调谐反褶积时窗．Fig．3 Windows of conventional deconvolution and Harmonizer deconvolution（a）Conventional deconvolution；（b）Harmonizer deconvolution．

3 应用实例

南美洲Oriente盆地属前陆盆地，含斜坡带低幅度油气构造，X 区块存在多套薄互层，目的层Y空间上存在明显泥岩墙构造，泥岩墙两边岩性差异经过多口钻井数据已证实．目的层Y 有效反射频率范围8～45 Hz，均方根速度3000m/s，全区较为稳定．处理目标主要落实Y 层等薄互层接触关系和砂泥岩边界．

预处理中通过简单区域高通滤波衰减面波和低频异常噪声后，在球面扩散振幅补偿基础上，采用地表一致性振幅处理方法，即地表一致性振幅补偿（SCAC）、异常振幅压制（ZAP）、地表一致性反褶积（SCDC），Kirchhoff叠前时间偏移（PSTM）叠加后沿Y 层提取负最大振幅值，泥岩墙见图4a所示，但横向边界不清晰，异常振幅存在．反褶积前应用反Q滤波补偿高频后，仍采用地表一致性反褶积再进行Kirchhoff叠前时间偏移，沿用上面方法提取Y 沿层属性，可以见到异常振幅得到压制，北西—南东向砂泥岩边界明显，见图4b．从叠加剖面和相应平均时频谱上也可以看到，深层高频信息明显增强，见图5．由此证明，反Q滤波在薄互层成像中补偿高频方面具有明显优势．

分析图4b属性图，平面属性中还存在多处“砂岩”异常块，横向分辨率不高．根据本文所述理论方法，对Kirchhoff叠前时间偏移加权因子进行修正．反掉球面扩散补偿因子，降低倾斜因子参数，根据偏移结果与测井曲线比较确定整形因子，重新进行叠前时间偏移处理，沿Y 层提取属性结果见图6，目的层同相轴与测井曲线对比见图7．从中可以看出，针对薄互层Kirchhoff叠前时间偏移可以不修正整形因子，关注球面扩散补偿因子和倾斜因子即可使偏移数据平面振幅属性和横向分辨率得到明显改善，砂泥岩薄互层平面振幅得到保护，平面砂泥岩边界变得更加清晰．

虽然利用地表一致性反褶积技术，可取得反射子波平面一致性，消除了部分近地表激发、接收对子波的影响，但薄互层纵向分辨率还是不高，叠加振幅谱一致性较差，剖面上还存在复波粘连现象，如图9a所示剖面及振幅谱．为了进一步分辨砂泥薄互层，在叠前时间偏移后CRP道集上采用子波调谐反褶积方法，以全区统一的子波算子长度和预测距离设计反褶积算子，进一步压缩地震子波、提高分辨率．子波调谐反褶积后属性如图8所示，可见泥岩墙边界保持完好、横向分辨率得以提高，砂岩位置清晰可靠，尤其是属性图左下方清晰出现更多较窄的泥岩墙，叠加剖面及叠加振幅谱见图9b，纵向分辨率也明显得到提高，横向断点干脆，频带展宽．此外，井旁道与井曲线对应关系吻合较好，见图10所示．

图10 工区井曲线与调谐反褶积应用前后井旁道对比Fig．10 Comparison of well log and uphole traces before and after Harmonizer deconvolution

通过以上三种关键方法有效地提高了X 区块薄互层资料的纵、横向分辨率，泥岩墙边界清晰．处理叠加体中薄互层、微幅构造等小尺度地质体成像可靠，可以开展后续的精细储层描述、测井约束反演、地震属性预测等，能够满足油田滚动勘探开发和岩性油气藏勘探的需要．

4 结 论

薄互层成像应该以岩性处理方法为基础，充分考虑偏移前、偏移过程中和偏移后子波频率特性变化，在不同处理阶段采用不同的处理方法才能精确识别砂泥岩薄互层和砂泥岩边界．因此，薄互层地震成像中高分辨率处理关键点包含以下三个方面：

（1）对于偏移前CMP道集，反Q滤波可以在不伤害反射的同时补偿高频衰减、提高地震子波平稳性，为后续的地表一致性反褶积创造假设条件，反Q滤波后空间振幅变化能够真实反映地下岩性变化，利于开展AVO 等岩性分析；

（2）Kirchhoff偏移过程中，选择最优加权函数有效地保护了地震子波频带，降低绕射叠加效应，偏移后波组特征保持良好，为砂泥岩边界、砂体分布刻划提供了保证；

（3）对于偏移后CRP 道集，若进行子波一致性处理或者继续提高分辨率应该考虑采用子波调谐反褶积方法，该方法能够在全区统一地震子波的约束下，设计反褶积算子，提高分辨率．

当然，薄互层成像与处理中的每一步都有直接关系，错误的观测系统定义、静校正、速度分析、提频处理和不合适的滤波增益都有可能导致薄互层成像失败或者保幅性失真．本文认为，在保真保幅处理前提下，在成像的不同阶段按照本文所述三种处理方法可以有效地提高薄互层纵、横向分辨率，提高薄互层成像精度．

致 谢 感谢东方地球物理公司研究院刘建宏、塔里木油田段文胜、法国CGG 地球物理公司刘俊杰给予的处理帮助，感谢中国地质大学（北京）地球物理与信息技术学院王志刚等博士们的解释、反演工作，他们为研究区泥岩墙成像提供了科学建议！

（References）

［1］ 高静怀，陈文超，李幼铭等．广义S变换与薄互层地震响应分析．地球物理学报，2003，46（4）：526－532．

Gao J H，Chen W C，Li Y M，et al．Generalized S transform and seismic response analysis of thin interbeds．ChineseJ．Geophys．（in Chinese），2003，46（4）：526－532．

［2］ 高静怀，万涛，陈文超等．三参数小波及其在地震资料分析中的应用．地球物理学报，2006，49（6）：1802－1812．

Gao J H，Wan T，Chen W C，et al．Three parameter wavelet and its applications to seismic data processing．ChineseJ．Geophys．（in Chinese），2006，49（6）：1802－1812．

［3］ Fu L，Wang J M，Cui F L，et al．3D AVO analysis for identifying thin continental sandstone interbeds and deep volcanic rocks．AppliedGeophysics，2005，2（1）：41－45．

［4］ Huang J B，Gao L J，Gao Y．Side lobes of wavelets impact identification of thin sand bodies．AppliedGeophysics，2007，4（2）：111－117．

［5］ Li Z S，Guo X B．Predicting the distribution of thin bed reservoirs by broad frequency band seismic．AppliedGeophysics，2007，4（2）：118－126．

［6］ Rayleigh J W S．The Theory of Sound，Vol．Ⅱ．Dover Publications Inc．，1945．

［7］ Ricker N．Wavelet contraction，wavelet expression，and the control of seismic resolution．Geophysics，1953，18（6）：769－792．

［8］ Widess M A．How thin is a thin bed？Geophysics，1973，38（8）：1176－1180．

［9］ Schoenberger M．Resolution comparison of minimum－phase and zero－phase signals．Geophysics，1974，39（6）：826－833．

［10］ Kallweit R S，Wood L C．The limits of resolution of zerophase wavelets．Geophysics，1982，47（7）：1035－1046．

［11］ Voogd N D，Rooijen H D．Thin－layer response and spectral bandwidth．Geophysics，1983，48（1）：12－18．

［12］ Robertson J D，Nogami H H．Complex seismic trace analysis of thin beds．Geophysics，1984，49（4）：344－352．

［13］ Juhlin C，Young R．Implication of thin layers for AVO studies．Geophysics，1993，58（8）：1200－1204．

［14］ Liu Y，Schmitt D R．Amplitude and AVO responses of single thin bed．Geophysics，2003，68（4）：1161－1168．

［15］ Berkhout A J．Seismic Resolution．London－Amsterdam：Geophysical Press，1984．

［16］ Safar M H．On the lateral resolution achieved by Kirchhoff migration．Geophysics，1985，50（8）：1091－1099．

［17］ Knapp R W．Vertical resolution of thick beds，thin beds，and bed cyclothems．Geophysics，1990，55（9）：1183－1190．

［18］ Chen J，Schuster G T．Resolution limits of migrated images．Geophysics，1999，64（4）：1046－1053．

［19］ Varela C L，Rosa A L R，Ulrych T J． Modeling of attenuation and dispersion．Geophysics，1993，58（8）：1167－1173．

［20］ Deng H L．Seismic wave propagation in thinly－layered media with steep reflectors［Master′s thesis］．Golden：Colorado School of Mines，1992．

［21］ Hargreaves N D，Calvert A J．InverseQfiltering by Fourier transform．Geophysics，1991，56（4）：519－527．

［22］ Hargreaves N D．Similarity and the inverseQfilter：some simple algorithms for inverseQfiltering．Geophysics，1992，57（7）：944－947．

［23］ Wu R S， Toksöz M N． Diffraction tomography and multisource holography applied to seismic imaging．Geophysics，1987，52（1）：11－25．

［24］ Tygel M T，Schleicher J，Hubral P．Pulse distortion in depth migration．Geophysics，1994，59（10）：1561－1569．

［25］ 钱荣钧．地震波的特性及相关技术分析．北京：石油工业出版社，2008．

Qian R J．Characteristics of the Seismic Waves and Related Technical Analysis（in Chinese）．Beijing：Petroleum Industry Press，2008．

［26］ Peacock K L，Treitel S．Predictive deconvolution：theory and practice．Geophysics，1969，34（2）：155－169．

［27］ Bancroft J C．A Practical Understanding of Pre/Poststack．Volume 1．SEG，2007．

［28］ Bancroft J C．A Practical Understanding of Pre/Poststack．Volume 2．SEG，2007．

［29］ Marfurt K J，Kirlin R L．Narrow－band spectral analysis and thin－bed tuning．Geophysics，2001，66（4）：1274－1283．

［30］ Robinson E A．Predictive decomposition of time series with application to seismic exploration．Geophysics，1967，32（3）：418－484．