基于谱元－简正振型耦合方法的核幔边界D″区地震波波形模拟方法研究

赵 明，赵 亮，Yann Capdeville

1 中国科学院地质与地球物理研究所 岩石圈演化国家重点实验室，北京 100029

2 中国科学院大学，北京 100049

3 Laboratoire de planétologie et de géodynamique de Nantes，CNRS，France

1 引 言

地球核幔边界D″区是一个构造复杂和强烈变化的区域，其中最重要的特征之一便是具有显著的地震波各向异性．通过对地震各向异性的观测研究，可以获取地球内部构造变形、动力学过程等信息．目前，地震学上主要采用横波分裂观测来研究D″区各向异性．比较常用的方法是测量地幔射线路径相似的横波震相如SKS－SKKS、S－ScS或Sdiff波的相对到时，这样可以校正台站端和震源端上地幔各向异性的影响，经过校正后的剪切波分裂时差δt和快轴方向φ可以认为代表了D″各向异性的大小和方向［2－3］．大多数相对走时分析的观测结果通常与垂直对称轴横向各向同性（简称VTI）介质结构相符［4－6］．

受地震和接收台站分布的影响，全球尺度D″区各向异性的地震学观测覆盖率和分辨率目前还很有限，存在的问题主要集中在两方面：有限的射线方位覆盖和上地幔各向异性校正的误差．因此一方面需要布设大规模密集宽频带数字地震台阵，另一方面还需要继续发展新的地震成像和计算方法提高观测的分辨率．特别是其中一个重要的研究方法是将正演模拟与波形分析相结合，以便更好地约束各向异性的几何形状，减少分裂时间分析中模型的不确定性［7］．对于边界形态、物质属性极为复杂的D″区而言，需要发展能够处理三维非均匀、各向异性介质复杂模型的高精度地震波波形模拟方法．

目前有着广泛应用的波动方程数值解法主要有：有限差分法［8］、谱方法、有限元法以及谱元法等．这些方法各有其优缺点：有限差分法以差分代替微分，算法简单，效率高，但其应用受到难以处理自由边界和复杂结构模型的限制；伪谱法在空间域基于快速Fourier变换或Chebyshev变换，精度高，空间频散小，收敛速度快，但是同样也只能处理简单模型结构和边界；有限元法虽然可以模拟任意复杂介质模型和适应自由边界，但其低阶方法存在严重数值频散，高阶方法存在伪波的问题，同时计算量很大；而谱元法是一种融合有限元法和伪谱法思想的方法，它保留了有限元处理边界和复杂结构的灵活性和伪谱法精度高并且快速收敛的优点，因此对于全球地震波模拟而言是一种比较理想的数值方法．谱元法经过近十几年的发展，其对复杂三维介质模型的模拟精度已经得到很好的检验，可以综合考虑各向异性、弹性衰减、速度和密度非均匀性、地球自转、重力、椭球率、地表起伏和海洋等因素［9－11］，被证明是一种在地震波全球和区域数值模拟中应用前景非常广阔的方法，其主要缺点在于计算量大，对计算资源的要求相当高．

为了充分地利用谱元法灵活处理三维复杂模型区域的优势，同时在保证计算结果精度的前提下尽可能控制运算量，Capdeville等提出一种将谱元法和经典解析解方法简正振型法耦合的方法——谱元－简正振型法［12］，同时设计了专门针对D″区展开研究的“sandwich”模型架构（图1），即只对核幔边界以上约300km 范围使用谱元法，对于D″区上下两个球对称区域采用计算需求更低的简正振型法计算［13］．两种方法采用DtN 算子耦合，其主要作用是：对给定的位移边界条件（又称Dirichlet边界条件），通过“DtN”算子可以计算对应边界处的牵引力（也称Neumann边界条件）［14］．耦合方法的计算效率和精度在“地球模拟器”上得到了很好的证实：对于各向同性PREM 模型计算大于8s周期的体波波形，配备128 个CPU 核、160GB 内 存，计 算2000s理论地震图需约28～29h．经过测试，对比全局的谱元方法，如SPECFEM3D对相同模型计算大于9s周期2000s长理论地震图，最低需要占用384个CPU核，538GB内存，模拟时间约16h．并且，随着模拟频率的增高，全局谱元法的计算需求还会呈指数级增长．尽管如此，目前Capdeville等的方法还只局限于针对非均匀各向同性介质，因此将该方法发展为能够模拟地震波在地球核幔边界D″地区各向异性介质中传播的数值方法具有十分重要的科学和实用意义．

2 问题描述和方法介绍

2．1 地震波波动方程

对初始处于静力学平衡状态的三维地球模型Ω，忽略地球自转，其地震波运动方程可写成如下形式：

ρ（r）为密度，随深度变化；r表示地球半径；u为位移场，其对时间的二阶导数记为ü；f代表震源，分点力源和矩张量震源的等效体力两种，后者可表示为：f（r，t）＝－Mərδ（r－r0）g（t－t0），其中M为矩张量，g（t－t0）为震源时间函数．

方程（1）中Κ定义为弹性－重力算符，包含弹性项和重力项，忽略地震波传播引起的地球质量重新分布效应［15］（又称柯林近似）后得到：

右端第一项为弹性项，T（u）表示弹性张量；右端第二项表示静力学平衡状态下只由重力引起的压力；右端第三项表示密度扰动引起的重力变化．

对于线弹性介质，（2）式中弹性张量T（u），根据胡克定律，有

其中Cijkl（i，j，k，l＝1，2，3）为广义弹性系数矩阵，该矩阵具有多种对称性，Cijkl＝Cjikl＝Cijlk＝Cklij．对于最一般的弹性各向异性介质，用21个独立弹性系数即可描述．此外，采用张量变换符号，可将四阶张量Cijkl变为二阶Cij（i，j＝1，2…，6）．

对于VTI介质，弹性系数矩阵为：

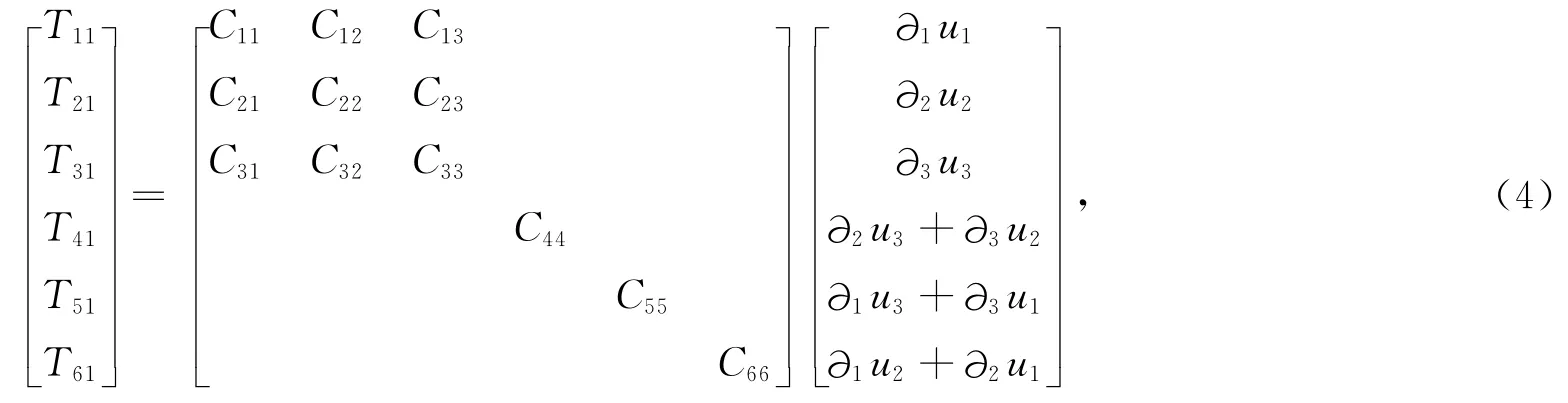
其中只有C11，C31，C33，C44，C66是独立参数，且与地震波速存在如下关系［16］：

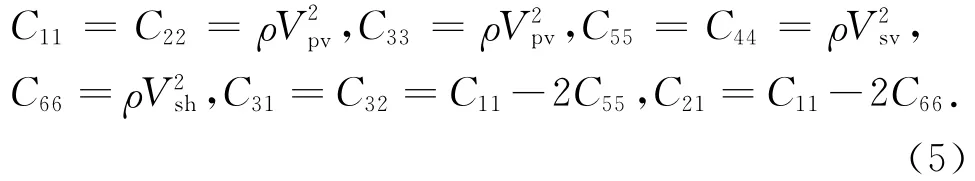
实际地球内的黏弹性介质会引起地震波衰减，Komatitsch等［17］用若干标准线弹性体的组合近似模拟地震波衰减效应，谱元－简正振型法沿用这一方案．

假定模拟开始时（t＝0）介质处于静止状态，则初始条件为：

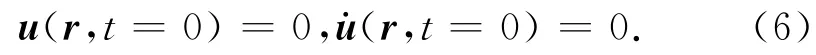
同时地表应满足自由边界条件：

此外，在不同计算区域的边界处需满足应力和位移连续条件（n表示外法向单位向量）．

固固边界Γ1（Ω1下边界，ΩD″上边界）：

固液边界Γ2（Ω2上边界，ΩD″下边界）：

2．2 空间域波动方程“弱”形式及求解简述

对于核幔边界D″区（记为ΩD″）采用谱元法计算，谱元法的求解基于方程（1）的“弱”形式：

w为任意测试向量；Γ－i（i＝1，2）代表ΩD″的上、下耦合边界，（·，·）为内积形式，例如

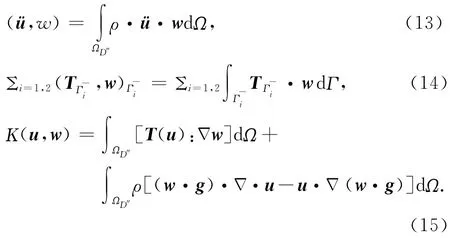
“弱”形式的初始条件变为：

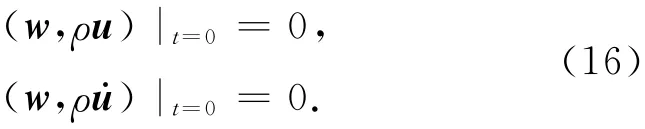
方程（12）的谱元法求解需要将模型区域ΩD″划分成一系列互不重叠单元Ωe，e＝1，2，…，n，且ΩD″＝Ωe．由于谱元法求解的单元是规则四边形或立方体，对于球壳状ΩD″，需要先建立“立方－球”映射，使得球壳可以分解为六个相同的立方体，再对每个立方体进一步划分成三维六面体网格计算［18］．接着对每个单元函数采用高阶Lagrange插值多项式近似，单元积分采用Gauss－Lobatto－Legendre（GLL）积分，积分点与插值点相同，从而可以形成对角质量矩阵简化运算［9－10］．

2．3 频率域求解

对D″区以上和以下的球对称区域Ω1（3850km＜r＜6371km）、Ω2（0＜r＜3480km），需要用简正振型法求解如下频率域波动方程：

根据Phinney等［19］，方程在球对称模型和给定位移边界条件下有解并能用广义球谐基函数γl，m（θ，φ）（l为角阶数，m为方位阶数）展开．考虑固固边界条件（8）的情形，其解的形式如下：

先不考虑方程（17）的右端项，将（18）代入（17），对每一个给定的角阶数l和频率ω，都能得到三个相互独立且符合初始正则性条件的解，其中两个为球振型，一个为扭振型，记为｛qdl（r，ω），q＝1，2，3｝．若方程（17）加上右端项，相应地可得到一个的特解，记为（r，ω）．此时方程（17）的解可写为：

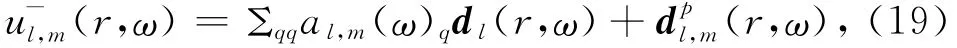
系数｛qal，m（ω），m∈［－l，l］｝的值随耦合边界条件（8）而定．

固液边界条件（10）、（11）下的求解过程与固固边界情形基本类似，不同之处在于只有一个满足条件的解dl（r，ω）．

2．4 边界耦合

在谱元法中对（13）式，即ΩD″边界的牵引力（i＝1，2）的计算需要用到“DtN”算子．“DtN”算子首先在频率域中建立，以固固边界耦合为例，对每一个角阶数l和频率ω，边界位移为（rΓ，ω），利用（19）式及连续性条件（11）都可得到对应的频率域“DtN”算子lD＋i（ω）及边界牵引力（rΓ，ω）值．

“DtN”算子在频率－波数域和时间－空间域建立的详细推导过程见Capdeville等［12］的文章．对位于频率域Ω1的震源和台站的影响，需要对“DtN”算子D＋1和地表位移引入额外的算子加以考虑，具体方法见Capdeville等［13］的附录．

2．5 并行执行

为得到具有足够分辨率的经过D″区的SKS、SKKS、S、ScS波形，观察其随模型改动产生的变化，本研究模拟的最短周期为6s，理论地震图计算时间为2000s，时间步长0．08s．为此对ΩD″划分9×9×6×6共2916 个六面体单元，单元采用6～8 阶Lagrange多项式插值．计算在中科院地球深部结构重点实验室基于OPENMPI并行技术的地球模拟器上调用128个CPU 核进行，约需36h．相比于谱元法，谱元简正振型方法由于只对核幔边界以上300km 左右区域使用谱元法，大大降低了数值模拟所需要划分的单元数量和计算资源使用量．

本研究所用谱元简正振型法为hsemm＿classic5．1［20］，并根据本研究需要拓展为能够模拟VTI介质．此外，对程序在mpi通信、网格生成速度方面分别做了优化，使得程序在地球模拟器上运行更为流畅．

3 方法验证

对表1所示的PREM 各向同性D″区模型（其中Cij值由（5）式推出），谱元简正振型耦合方法与简正振型法已经做过对比验证，二者计算结果相当一致［21］．

表1 PREM 模型D″区参数Table 1 Parameters of PREM model′s D″area

为了证明本研究对hsemm＿classic5．1各向异性拓展的有效性，在此基础上设置了如表2 所示各向异性参数ξ＝≈1．3的VTI－PREM 模型，并使用拓展方法与简正振型法进行对比验证．

表2 VTI－PREM 模型D″区参数Table 2 Parameters of model VTI－PREM model′s D″area

由于对小于8s周期的球振型理论地震图简正振型法计算结果尚不够理想［22］，本文只对比两种方法在8s时的计算结果．对比所用震源时间函数如图1a所示，其中拐角频率ωc≈0．13Hz（图1b）决定了模拟的最短周期为8s．计算结果如图2所示，在震中距为65°时，三分量上二者波形几乎没有差别，当震中距为125°时，噪音会相应增加，但不影响震相的匹配程度．值得一提的是从算法角度说，本文采用的PREM 和VTI－PREM 模型可以看做径向分层、横向均匀的三维模型，其在hsemm＿classic中的代入处理上与三维模型一致，因此验证该方法对一维模型的计算精度实际上也验证了该方法对三维模型的计算精度［23］．

图1 对比所用的Heavis震源时间函数（a）及其振幅谱（b），拐角频率0．13Hz（约8s）．Fig．1 （a）The Heavis source－time function used for benchmark between CSEM（coupled spectral element method with mode）and NMS（normal mode summation）method；（b）The corresponding source spectrum to the left．The central frequency is 0．07Hz and the corner frequency is 0．13Hz（～8s）．

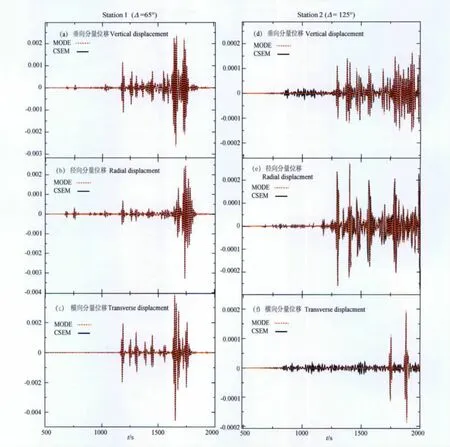
图2 简正振型法（红）和耦合CSEM 方法（黑）分别对VTI－PREM 模型计算得到的三分量理论地震图对比．（a）（b）（c）台站震中距为65°，三分量震相到时和振幅上符合很好；（d）（e）（f）台站震中距为125°，随着震中距增大，CSEM 方法的噪音增大，但主要震相符合得很好Fig．2 Comparison between NMS（red）synthetics and CSEM synthetics（black）in three components（Z，R，T）．（a）（b）（c）Epicenter distance 65°，the waveforms match perfectly in both arrival time and amplitude；（d）（e）（f）Epicenter distance 125°，the noise of CSEM result increases，but the amplitude and arrival time still match very well

4 一维各向异性模型中的S、ScS、SKS波形模拟

本研究应用VTI－PREM 模型，同时选取震源深度分别为312．6km（模拟S－ScS）和612．4km（模拟SKS－SKKS）的两个地震事件（图3），并采用更简单的Gauss震源时间函数（图4），探讨D″区在VTI各向异性情形下S，ScS，SKS、SKKS 波的传播和变化．

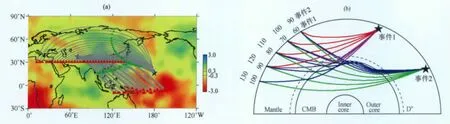
图3 （a）事件1和事件2，震源深度分别为612．4km 和312．6km，台站震中距范围分别为60°～130°和65°～90°，背景为CMB附近S波层析成像图［24］；（b）S，ScS，SKS二维走时路径图［25］（图中数字为震中距，单位°）Fig．3 （a）A map of two events used for waveform modelling．The depths of the two events are 612．4km and 312．6km，seperately，and the epicenter distances range from 60°～130°and 65°～90°，seperately；（b）The ray paths of S（red），ScS（purple），SKS（green），SKKS（blue）．

图4 各向异性模拟所用的高斯震源时间函数（a）及震幅谱（b），拐角频率为0．125Hz（8s）Fig．4 （a）Gauss source－time function used for the anisotropic modelling．The source－time function is similar to a triangle with half－duration of 8s；（b）Spectral amplitude of the source，the corner frequency is 0．125Hz．

4．1 S，ScS震相

在VTI－PREM 模型中，预设波在VTI各向异性介质中平均SV 速度（6．265km·s－1），在核幔边界以上150km 范围比SH 速度（7．265km·s－1）慢1km·s－1，ξ≈1．3．模拟结果印证了这一点：如图5，S震相的径向和横向分量在震中距范围65°～90°到时和波形基本一致，这主要是因为S震相没有通过各向异性D″区；而ScS的横向分量比径向分量在震中距65°～74°及82°～95°都更早出现，这反映了ScS震相通过各向异性D″区引起的S波分裂效应．

图5 VTI－PREM 模型计算得到的理论地震图SV（红虚）与SH（黑）位移分量对比，按S参考到时排列并对波形自归一，截取S震相以后100s．震中距范围65°～90°，共18台站Fig．5 Synthetic displacement seismograms of SH（black）and SV （red）components for the VTI－PREM model，aligned by S arrival predicted by PREM and each seismogram self－normalized by its maximum amplitude．The epicenter distances of the 18stations range from 65°～90°．

4．2 SKS和SKKS震相

从图6（a、c）看，VTI－PREM 模型计算的理论地震图SKS、SKKS径向分量相比各向同性情形的SKS（ref）、SKKS（ref）都发生了延迟，而横向分量上（图6（b、d））则没有明显的SKS、SKKS震相出现．这主要有两种可能的原因：一是由于SKS、SKKS且快速近垂直穿过D″区，这么短的路径和时间里很难发生显著的分裂现象；二是SKS、SKKS均为外核内的P波在核幔边界转换成的SV波，而在VTI介质情形下，径向偏振的S 波几乎不会发生分裂．如果要讨论SKS 和SKKS的横向分量及变化，还需要考虑介质的方位角各向异性进行模拟，这将在今后下一步的工作中完成．

图6 VTI－PREM 模型计算得到的理论地震图径向分量和横向分量：（a）（b）按SKS参考到时排列并对波形自归一，截取SKS震相以后100s，震中距范围90°～120°，共10台站；（c）（d）按SKKS参考到时排列并对波形自归一，截取SKKS震相以后100s，震中距范围90°～130°，共14台站Fig．6 Synthetic displacement seismograms of radial components and transverse components for the VTI－PREM model：（a）（b）aligned by SKS arrival predicted by PREM and each seismogram self－normalized by its maximum amplitude．The epicenter distances of the 10stations range from 90°～120°；（c）（d）aligned by SKKS arrival predicted by PREM and each seismogram self－normalized by its max amplitude．The epicenter distances of the 14stations range from 90°～130°

5 讨 论

本研究扩展了Capdeville等提出的并行谱元－简正振型方法，使其具备了模拟垂直对称轴各向异性介质的功能，与经典解析解方法简正振型法的对比证明了该扩展的有效性．应用新程序，模拟了VTI－PREM 模型下的SV 和SH 波形变化，所得到的分裂结果正确反映了介质结构的变化．其中对SKS波的模拟显示，VTI介质情形下的D″区会引起SKS波在径向分量上的快慢变化，而不会引起横向分量上的变化，如果要观测到SKS和SKKS的横向分量变化，需要进一步模拟方位角各向异性介质结构下（如TTI）的S波分裂现象．

目前D″区实际观测认为该区在核幔边界以上约300km 范围S波各向异性强度总体而言dlnξ＜3%［26］，从数值模拟角度而言这属于较“弱”的各向异性，需要计算的地震波最短周期为1～2s，是一项颇具挑战性的工作．其最大的困难主要来自两方面：一是简正振型方法在球振型计算上的局限，其低于7～8s周期的结果会出现很多噪音，不过近几年简正振型法方法上和理论上都有很大改进，为谱元简正振型耦合方法对更高频率的应用提供了新的发展空间［27－28］；二是计算量相当大，全球模拟需要用到大规模并行计算，对计算机软硬件投入很大，目前尚不具备普遍开展此项研究的条件．单独从方法的角度说，谱元法对于模拟的最短周期并没有任何限制，因此随着计算机技术的飞速发展，谱元法必将在核幔边界各向异性模拟中发挥更大的作用．

6 结 论

本文将一种用于模拟核幔边界D″区非均匀性模拟的数值模拟方法——谱元简正振型法扩展为各向异性，并通过与简正振型方法的对比验证，证明谱元简正振型方法对于＞8s频率的理论地震图计算模拟结果是可靠的．同时对VTI介质结构模型的计算模拟，表明谱元－简振振型法可以模拟各向异性介质中的体波波形变化．下一步的工作将比较方位角各向异性介质中SV 和SH 波形的不同，并将模拟提升到更高频率，以应对精确模拟S波分裂现象的需求．

致 谢 感谢何玉梅博士提供的画图程序以及与罗玉来进行的有益探讨；感谢中国科学院地质与地球物理研究所深部结构重点实验室提供Earth 模拟器；感谢Earth模拟器负责人张志刚博士在并行计算中提供的帮助．

（References）

［1］ Dziewonski A M，Anderson D L．Preliminary reference Earth model．Phys．EarthPlanet．Inter．，1981，25（4）：297－356．

［2］ Thomas C，Kendall J M．The lowermost mantle beneath northern Asia－II．Evidence for lower－mantle anisotropy．Geophys．J．Int．，2002，151（1）：296－308．

［3］ Wookey J，Kendall J M，Rümpker G．Lowermost mantle anisotropy beneath the north Pacific from differential S－ScS splitting．GeophysicalJournalInternational，2005，161（3）：829－838．

［4］ Nowacki A，Wookey J，Kendall J M．New advances in using seismic anisotropy，mineral physics and geodynamics to understand deformation in the lowermost mantle．J．Geod．，2011，52（3－4）：205－228．

［5］ 杨凤琴，刘斌，倪四道等．西伯利亚下地幔底部的剪切波各向异性．地震学报，2008，30（2）：209－213．

Yang F Q，Liu B，Ni S D，et al．Shear velocity anisotropy of the lowermost mantle beneath the Siberia．ActaSeismologica Sinica（in Chinese），2008，30（2）：209－213．

［6］ 戴志阳，刘斌，王宵翔等．西太平洋下D″区的剪切波各向异性．地震学报，2007，29（5）：459－466．

Dai Z Y，Liu B，Wang X X，et al．Shear wave anisotropy in D"region beneath the western Pacific．ActaSeismologica Sinica（in Chinese），2007，29（5）：459－466．

［7］ 戴志阳．西太平洋下地幔D"层的地震波速度各向异性研究［博士论文］．合肥：中国科学技术大学，2008．

Dai Z Y．Seismic velocity anisotropy in D′layer of mantle beneath the Western Pacific（in Chinese）［Ph．D．Thesis］．Hefei：University of Science and Technology of China．

［8］ Zhao L，Wen L X，Chen L，et al．A two－dimensional hybrid method for modeling seismic wave propagation in anisotropic media．J．Geophys．Res．，2008，113：B12307，doi：10．1029/2008JB005733．

［9］ Komatitsch D，Tromp J．Spectral－element simulations of global seismic wave propagation－I．Validation．Geophys．J．Int．，2002，149（2）：390－412．

［10］ Komatitsch D，Tromp J．Spectral－element simulations of global seismic wave propagation－II．3－D models，oceans，rotation and self－gravitation．Geophys．J．Int．，2002，150（1）：303－318．

［11］ Liu Q，Polet J，Komatitsch D，et al．Spectral－element moment tensor inversions for earthquakes in southern California．Bull．Seismol．Soc．Am．，2004，94（5）：1748－1761．

［12］ Capdeville Y，Chaljub E，Vilotte J P，et al．Coupling the spectral element method with a modal solution for elastic wave propagation in global earth models．Geophys．J．Int．，2003，152（1）：34－66．

［13］ Capdeville Y，To A，Romanowicz B．Coupling spectral elements and modes in a spherical Earth：an extension to the＇sandwich＇case．Geophys．J．Int．，2003，154（1）：44－57．

［14］ Givoli D，Keller J B．Non－reflecting boundary conditions for elastic waves．WaveMotion，1990，12（3）：261－279．

［15］ Chaljub E，Komatitsch D，Vilotte J P，et al．Spectralelement analysis in seismology．∥ Wu R S，Maupin V．Advances in Geophysics，Advances in Wave Propagation in Heterogeneous Earth．San Diego：Elsevier Academic Press Inc．，2007，48：365－419．

［16］ Love A E H．A Treatise on the Mathematical Theory of Elasticity．New York：Dover Publications，1944．

［17］ Komatitsch D，Vilotte J P，Vai R，et al．The spectral element method for elastic wave equations：application to 2D and 3D seismic problems．InternationalJournalfor NumericalMethodsinEngineering，1999，45：1139－1164．

［18］ Ronchi C，Ianoco R，Paolucci P S．The Cubed Sphere：a new method for the solution of partial differential equations in spherical geometry．J．Comput．Phys．，1996，124（1）：93－114．

［19］ Phinney R A，Burridge R．Representation of the elasticgravitational excitation of a spherical earth model by generalized spherical harmonics．GeophysicalJournal International，1973，34（4）：451－487．

［20］ To A，Romanowicz B，Capdeville Y，et al．3D effects of sharp boundaries at the borders of the African and Pacific superplumes：Observation and modeling．EarthPlanet．Sci．Lett．，2005，233（1－2）：137－153．

［21］ Qin Y L，Capdeville Y，Montagner J P，et al．Reliability of mantle tomography models assessed by spectral element simulation．GeophysicalJournalInternational，2009，177（1）：125－144．

［22］ Dahlen F A，Tromp J．Theoretical Global Seismology．Princeton：Princeton University Press，1998．

［23］ Komatitsch D，Vinnik L P，Chevrot S．SHdiff－SVdiff splitting in an isotropic Earth．J．Geophys．Res．，2010，115（B7）：B07312．

［24］ Grand S P．Mantle shear－wave tomography and the fate of subducted slabs．Philosophical Transactions of the Royal Society of London．Series A：Mathematical．Physicaland EngineeringSciences，2002，360（1800）：2475－2491．

［25］ He Y M，Wen L X，Zheng T Y．Geographic boundary and shear wave velocity structure of the"Pacific anomaly"near the core－mantle boundary beneath western Pacific．EarthandPlanetaryScienceLetters，2006，244（1－2）：302－314．

［26］ Panning M，Romanowicz B．A three－dimensional radially anisotropic model of shear velocity in the whole mantle．GeophysicalJournalInternational，2006，167（1）：361－379．

［27］ Yang H Y Y，Zhao L，Hung S H．Synthetic seismograms by normal－mode summation：a new derivation and numerical examples．GeophysicalJournalInternational，2010，183（3）：1613－1632．

［28］ Al－Attar D，Woodhouse J H，Deuss A．Calculation of normal mode spectra in laterally heterogeneous earth models using an iterative direct solution method．GeophysicalJournal International，2012，189（2）：1038－1046．