采用低分辨率空间光调制器的大尺寸高像质空中三维立体成像

李志扬，Havyarimana Claver，李亚兰

(华中师范大学物理科学与技术学院，武汉430079)

大尺寸、高像质空中三维立体成像是三维立体显示技术的未来发展方向。要实现空中立体成像目前可采用集成成像技术，也可采用全息技术。其中集成成像属于非相干成像技术，而全息成像属于相干成像技术。两者的一个关键差别在于前者只利用了光波的振幅信息，而后者既利用了光波的振幅信息，也利用光波的位相信息，因而人们称其为全息技术。振幅主要反映物体的亮度信息，物体的形状和空间位置信息体现在位相中。集成成像技术通过几何光学方法采用微透镜阵列记录和再现物体不同角度的图像，由于微透镜的景深和像质有限，使得集成成像系统的分辨率和视场景深受到很大限制［1－3］。全息技术通过物理光学方法借助参考光记录和再现物光，仅需一块全息干板，不再需要其他光学或机械扫描系统［4］。对于大尺寸、高像质立体成像，全息干板的分辨率需要达到每毫米数千线对以上，这个分辨率远远大于目前平板显示器的分辨率，因此给动态全息显示造成了很大障碍。目前人们试图通过降低干涉条纹的密度实现动态全息显示，例如很多研究者报道了采用投影液晶片实现远离屏幕的小物体的全息动态显示［5－6］。

最近笔者提出了一种新的产生光学波前的方法［7］，即数字光学位相共轭方法，它彻底放弃了参考光，因此不再需要记录和再现高密度干涉条纹。其核心思想是直接把复杂光波分解为离散的简单光波，而这些简单离散光波可用现有低分辨率空间光调制器产生。由于光路的可逆性，这些数字化实时产生的简单光波逆向传播，可以以衍射极限分辨率合成出任意复杂光波，这些复杂光波在空中展开，再借助一套光学转换系统，就可形成大尺寸、大观察角、高像质三维立体图像。笔者对上述基于数字光学位相共轭原理的实时三维立体成像方法进行了分析讨论。

1 数字光学位相共轭基本原理

光学波前形状相同而传播方向相反的两个光波其复振幅呈共轭关系。传统的光学位相共轭方法借助非线性光学效应，如四波混频、受激布里渊散射等［8－9］，对入射光进行反射，使其复振幅产生共轭变换，由于光路的可逆性，不管沿途经历过什么变形，该光波原路返回，达到起始点时又恢复出原始波前形状。上述传统光学位相共轭方法必须借助非线性光学介质，且只是反射已经存在的入射光，因此不能用于数字化产生任意复杂光学波前。为实现数字光学位相共轭，笔者构思了一种绝热锥形单模光波导束，即图1中的Taper，它由许多单模光波导组成，在图中左侧细端这些单模光波导彼此耦合，从左至右，单模光波导之间的间隔逐步加大，直至在右侧粗端彼此隔离。当光波从左侧入射到绝热锥形光波导束的细端时，它被逐步分离引导到每根单模光波导的芯层，最后从粗端出射。由于单模光波导的输出模场分布恒定，当左侧输入光波场改变时，右侧从每根单模光波导输出的光波场仅改变其振幅和位相，模场分布形状不变。采用图1右侧的组合式空间光调制器，即图1中的SLM，可对从右侧入射的平行照明光进行逐像素调节，并通过微透镜阵列，即图1中的MLA，把调节后的光波聚焦到每根单模光波导的芯层。如果在每根单模光波导的芯层通过SLM实时数字重建的光波场恰好与入射光波引起的光波场成共轭关系，则通过实时数字重建的光波将会沿输入光波的传播路径原路返回，由于光路的可逆性，完整地合成恢复出原始输入光波。

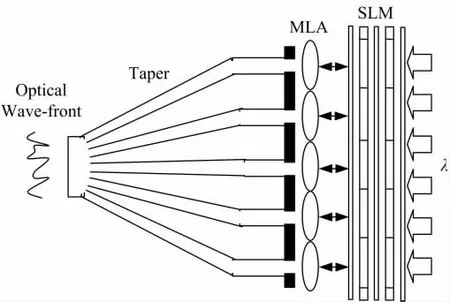
图1 实现数字光学位相共轭的装置Fig.1 Device to perform digital optical phase conjugation

2 基于数字光学位相共轭原理的三维立体成像系统

2.1 光路结构与工作原理

观察者看到空中有一个物点是因为该物点向四面八方发射出光波，或者说该物点发出的光波在空中形成一个光锥，锥顶所在位置即为物点所在位置。如果能采用某种方式在空中形成一个光锥，站在该光锥内的观察者同样会认为锥顶所在位置存在一个物点，只要观察者不亲手触摸锥顶，该观察者无法分辨在锥顶位置是否存在一个真实发光物点。根据这种等同性原理，可在空中不同位置形成许许多多光锥，从而组成一幅离散三维立体图像。

图2给出了一种在空中不同位置产生光锥的光学系统，其关键部件是如图1所示的一个数字光学位相共轭装置，图2中用Taper表示。如果采用高清SLM，Taper细端的直径在1 mm量级，因此把Taper的细端放置在图2中透镜LensA的焦点附近，这样在Taper细端附近实时数字重建的光波经透镜LensA转换成一个非均匀平行光束，该平行光束经图2中的微透镜阵列MLA的再聚焦，在每一个微透镜的焦点处形成一个光锥，组成一个光锥阵列，从该光锥阵列发出的光把MLA前方整个空间照亮，即在MLA前方某一点，可接收到来自许许多多微透镜焦点的光线。

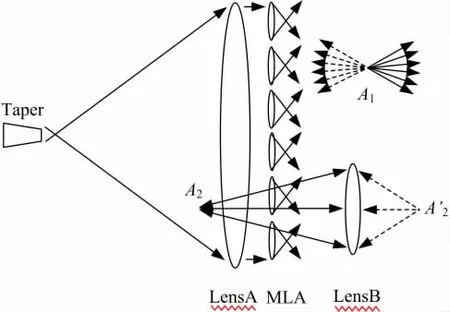
图2 基于数字光学位相共轭的三维成像系统Fig.2 3D imaging system based on digital optical phase conjugation

图2所示三维立体成像系统其工作原理仍然基于数字光学位相共轭原理。其工作过程可分为两步:1)逐点标定。把整个三维立体成像空间划分成许多离散网格，把一个点光源分别放置在每个格点，例如图2中A1点。从A1点光源发出的光线(图2中虚线)从右向左传播，分别经过MLA和LensA，其中一部分进入Taper细端，记录下从Taper的粗端出射的光波场的复振幅。2)逐点相加。如果仅需在A1点产生一个光点，把1)中记录的对应A1点的光波场复振幅取共轭，然后通过图1所示SLM实时产生该共轭光波，由于光路的可逆性，该共轭光波逆向通过Taper，从Taper细端出射，并沿路返回，在A1点重建一个光锥(图中实线)，这样在空中就形成了一个体元(Voxel)。类似地由许许多多Voxel就可形成一幅离散立体图像，当然此时在第2步中需要把对应各个Voxel所在格点处记录的光波场复振幅，根据该Voxel的亮度逐点比例相加，最后再把总光场取共轭。

图2所示成像系统不仅可在MLA前方产生立体实像，也可在MLA后方产生立体虚像。为产生立体虚像，或者说虚Voxel，可在第一步逐点标定中，借助一个辅助透镜LensB把A'2点处的点光源投射到MLA背后的A2点，如图2中虚线所示。如果保持LensB位置不变，经过重建，由于光路的可逆性可在A'2点产生一个实光点，但是如果拿走LensB，所有重建光线看上去都象是从MLA背后的A2点发出的(图2中实线)，这样就可在MLA后方产生立体虚像。立体虚像的产生扩展了三维立体成像范围。

2.2 三维成像区域与观察视角

在图2中，从Taper细端发出的光波经透镜LensA转换成一个非均匀平行光束，该平行光束经图2中的微透镜阵列MLA再聚焦，在每一个微透镜的焦点处形成一个光锥，该光锥锥角取决于微透镜的焦距与口径之比，记为2α。采用现代加工工艺，2α可大于90度。如图3所示，在微透镜阵列MLA前方任一点，到达该点的来自不同微透镜的焦点处的光线组成的夹角最大为2α。以微透镜阵列MLA的上下边缘为中心，分别作与水平线角度为±α的射线(图3中虚线)，该射线把整个垂直平面划分为九个区域，这9个区域根据其性质可分为3类。同时在每一个成像点，以该点为中心分别作与水平线角度为±α的射线(图3中实线)，如果该射线超过MLA的边缘，则放弃该射线，并连接该点与MLA的边缘，最后所得两条实线之间的夹角就代表了到达该点的光线所能组成的最大夹角，或者说在该点重建产生的Voxel所发出的光锥的锥角。

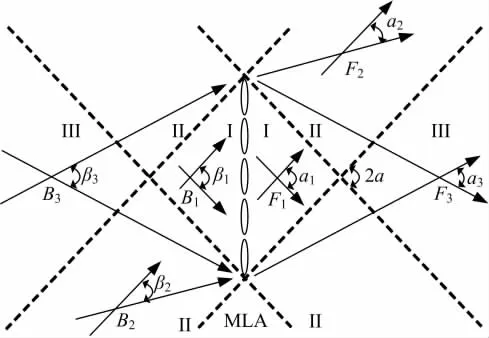
图3 三维成像区域Fig.3 3D image form ing area

由图3可知，在Ⅰ区域内的每一点F1、B1，重建产生的光锥锥角α1=2α，β1=2α;在Ⅱ区域内的每一点F2、B2，重建产生的光锥锥角α2≤2α，β2≤2α;而在Ⅲ区域内的每一点F3、B3，重建产生的光锥锥角α3≤2α，β3≤2α。由于观察者只有站立在某个 Voxel发出的光锥锥角内才能看到该Voxel，因此上述光锥锥角等同于观察视角。

如果以观察者的站立位置为中心分别作与水平线角度为±α的射线，如果该射线超过MLA的边缘，则直接连接观察者的站立位置与MLA的边缘，最后所得两条实线围成一个区域，位于该区域内的所有Voxel对站在该区域顶点位置的观察者来说是可见的。这意味着MLA相当于一块窗玻璃，观察者可观察到位于MLA后，且横截面积数十倍于MLA的立体虚像，也可观察到位于MLA前，且横截面积小于MLA的立体实像。

2.3 立体图像分辨率

在图2中，假设位于MLA前方焦平面的光场分布为U0(x'，y')，根据基尔霍夫衍射公式，在MLA焦平面前方Z处的光场分布U(x，y)可写为

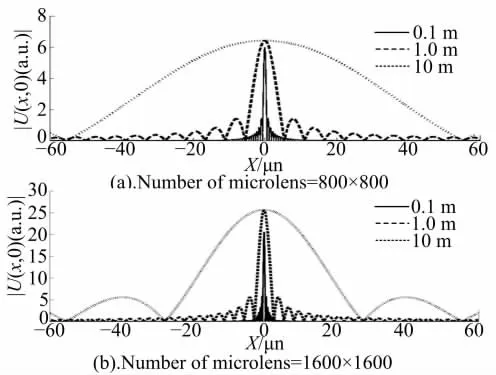
图4 不同面积M LA在不同成像距离的分辨率Fig.4 Distribution of|U(x，0)|at Z=0.1，1 and 10m using M LA w ith different areas

3 结论

综上所述，笔者提出了一种基于数字光学位相共轭原理的空中三维立体成像方法，它无需借助参考光记录和再现物光，而是通过一个绝热锥形单模光波导束直接对物光进行分解和数字重建，由于不涉及全息技术中的高密度干涉条纹，它可采用现有低分辨率空间光调制器。类似于全息技术，它既利用了光波的振幅信息，也利用了光波的位相信息。更关键的是它利用光路可逆性原理消除了传统光学透镜系统的像差和景深限制，可实现大范围、大视角空中立体成像，无论屏幕前的立体实像和屏幕后的立体虚像都可以象观看真实物体一样多人同时自然观看。计算表明上述系统即使采用一块尺寸为100×100 mm2的MLA，在其前方0.1 m，1 m，10 m处所显示的立体图像的分辨率分别可达到1μm，11μm，112μm，优于普通液晶平板显示器。

［1］Lippmann M G.Epreuves reversibles donnant la sensation du relief［J］.JPhys，1908(7):821－825.

［2］Martnez－Corral M.Integral imaging with improved depth of field by use of amplitude modulated microlens array［J］.Appl Opt，2004，43(31)，5806－5813.

［3］王琼华.3D显示技术与器件［M］.北京:科学出版社，2011.

［4］周海宪，程云芳.全息光学［M］.北京:化学工业出版社，2006.

［5］Christian Kohler.Optimally tuned spatial lightmodulators for digital holography［J］.Appl Opt，2006，45 (31):960－967.

［6］Yara F，Kang H，Onural L.State of the art in holographic displays:A survey［C］//IEEE/OSA Journal of Display Technology 2010:443－454.

［7］Li Zhi－yang.Accurate optical wavefront reconstruction based on reciprocity of an optical path using low resolution spatial light modulators［C］//Opt Communications，2010:3646－3657.

［8］陈军.光学位相共轭及其应用［M］.北京:科学出版社，1999.

［9］刘思敏，许京军，郭儒，相干光学原理及应用［M］.天津:南开大学出版社，2001.