磁悬浮永磁直线电动机悬浮系统模糊PID控制器的设计

蓝益鹏，邱超

(沈阳工业大学电气学院，辽宁沈阳110870)

直线伺服进给技术在数控机床中的应用，消除了传统机械传动链带来的一系列不良影响，极大地提高了进给系统的快速反应能力和运动精度。然而数控机床加工中的摩擦阻力，特别是在低速时的非线性摩擦，不可避免地影响伺服系统的精度，导致进给系统产生爬行以及造成反向死区。此外摩擦也是引起数控机床热变形的原因之一。因此，如何有效地减小或消除摩擦引起了普遍的关注。

在此采用一种新型磁悬浮永磁直线同步电动机的结构，以消除动子与导轨之间的摩擦，该直线电机在电机动子中放置有两套具有相同极对数的绕组，其中一套用于产生电磁推力;另一套用于产生磁悬浮力。通过控制悬浮绕组的电流，改变磁场在气隙中的分布，实现进给平台的稳定悬浮运行［1］。

应用矢量控制方法可以实现推力与悬浮力的解耦，从而可以对悬浮子系统进行独立控制。因为悬浮系统本身是一个非线性系统，且难以建立精确的数学模型，因此传统的方法很难达到控制要求。为保证悬浮控制的高精度、高鲁棒性，通过设计模糊PID控制器使悬浮控制系统具有良好的跟随性能和抗扰性能，仿真结果验证了该控制方法的有效性。

1 悬浮子系统的数学模型

假定Ld=Lq=L，采用iq=0的控制策略，那么，磁悬浮永磁直线同步电动机悬浮子系统在d-q坐标系的非线性数学模型可描述如下［2-4］:

电压方程:

悬浮力方程:

动力学方程:

式中:ud、uq分别为d、q轴电压;id、iq分别为d、q轴电流;Rs为动子电枢绕组电阻;ψd、ψq为电枢绕组d、q轴磁链;δ为气隙高度;μ0为真空磁导率; lFe为定子铁心和动子铁芯中磁路的等效总长度;μFe为铁芯的磁导率;μM为永磁体的磁导率。

2 模糊PID控制器设计

由于悬浮系统的非线性以及外部干扰的不确定性，设计一套模糊PID控制器用于系统的位移闭环。根据经验选择二维的模糊控制器，模糊PID控制器的结构如图1所示［5-6］。

图1 模糊PID控制器结构图

由图1可知输入量与反馈量的偏差e和偏差变化率ec乘以量化因子转换成模糊控制器的两个输入，然后经过模糊推理、解模糊化、乘以比例因子转换为PID控制器中比例、积分、微分系数的变化量ΔKp、ΔKi、ΔKd，与初始PID参数相加得到新的PID参数，然后通过PID控制器计算出控制量u(t)，对被控对象进行控制。

2.1 模糊化和隶属函数的建立

取输入e、ec和输出ΔKp、ΔKi、ΔKd，模糊子集为{NB，NM，NS，ZO，PS，PM，PB}，子集中元素分别代表负大、负中、负小、零、正小、正中、正大，其论域为［-3，3］。在模糊逻辑工具箱的隶属度函数编辑器中，选择输入量e、ec的隶属函数为高斯型 (Gaussmf)，输出ΔKp、ΔKi、ΔKd的隶属函数为三角形 (Trimf)，如图2和图3所示［7］。

图2 e及ec隶属度函数

图3 ΔKp、ΔKi、ΔKd隶属度函数

2.2 模糊化规则的建立

根据参数Kp、Ki、Kd对系统输出特性的影响，可归纳出系统在被控过程中对不同的偏差和偏差变化率，参数Kp、Ki、Kd的自整定原则［8］:

(1)当偏差较大时，为了加快系统的响应速度，并防止因开始时偏差的瞬间变大可能引起的微分过饱和而使控制作用超出许可范围，应取较大的Kp和较小的Kd。另外为防止积分饱和，避免系统响应出现较大的超调，Ki值要小;

(2)当偏差和变化率为中等大小时，为了使系统响应的超调量减小和保证一定的响应速度，Kp应取小一些。在这种情况下，Kd的取值对系统影响很大，应取小一些，Ki的取值要适当;

(3)当偏差较小时，为了使系统具有较好的稳态性能，应增大Kp、Ki值，同时为避免输出响应在设定值附近振荡，以及考虑系统的抗干扰能力，应适当选取Kd。其原则是:当偏差变化率较小时，Kd取大一些;当偏差变化率较大时，Kd取较小的值，通常Kd为中等大小。

从而得到的模糊控制规则见表1—3。

表1 ΔKp的模糊控制规则表

表2 ΔKi的模糊控制规则表

表3 ΔKd的模糊控制规则表

2.3 推理算法和解模糊化算法的设计

在MATLAB命令窗口运行Fuzzy进入模糊逻辑编辑器，并建立一个新的FIS文件，选择控制器类型Mamdani，推理 (Implication)方法选为min，解模糊化 (Defuzzification)方法为重心平均法centroid，如图4所示。

图4 清晰化的方法

3 仿真研究

用MATLAB对磁悬浮永磁直线同步电动机磁悬浮系统进行仿真，仿真模型见图5、6。

图5 模糊PID控制器仿真模型

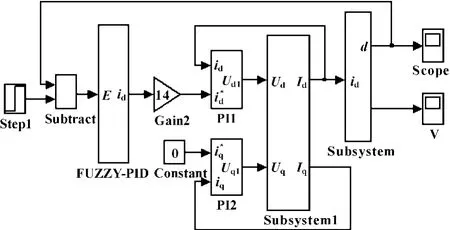
图6 模糊PID控制系统仿真图

模糊化因子Ke=3，Kec=12，解模糊因子K1=5，K2=2，K3=1，PID初始值Kp=100，Ki=8，Kd= 30。

磁悬浮永磁直线同步电动机主要参数如下:

m=30 kg，L2d+Lmd=34.81 mH，R2s=0.895 5 Ω，np=3，τ=33 mm，fy=100 N。在t=0.4 s时加载，位置参考输入δ*=5 mm，额定速度v=0.66 m/ s，推力绕组，额定电流i1q=1.76 A。

系统输入信号为5 mm的阶跃信号，仿真结果如图7—9所示。

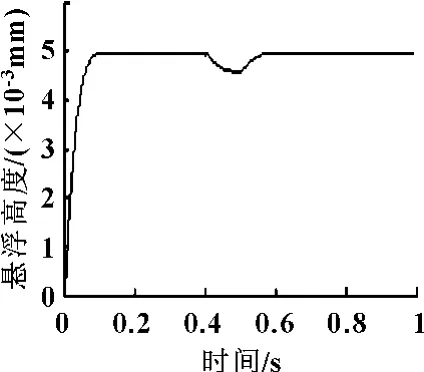
图7 悬浮高度曲线

图8 电流曲线

图9 位置误差曲线

由图7可知:悬浮高度迅速收敛于参考输入δ*=5 mm，系统上升时间和调节时间短，超调量小，表明系统具有良好的跟随性能。

在t=0.4 s时，突加负载干扰fy=100 N，图8、9分别为系统悬浮绕组电流曲线和高度误差曲线，可知:扰动作用下系统恢复时间短，动态降落小，表明系统有较强的抑制扰动能力。

4 结论

针对数控机床直线电动机驱动系统中动子与静止导轨之间的摩擦问题，采用磁悬浮永磁直线同步电动机来实现无摩擦进给。悬浮系统本身是一个非线性系统，且难以建立精确的数学模型。为保证悬浮控制的高精度、高鲁棒性，设计了模糊PID控制器。仿真结果证明:该控制器起到良好的抗干扰作用，系统的跟踪误差小，响应速度快，可以保持悬浮系统的稳定性。

【1】田录林，张靠社，王德意，等.永磁导轨悬浮和导向磁力研究［J］.中国电机工程学报，2008，28(21):135-139.

【2】蓝益鹏，赵辉，李成军.进给平台永磁直线磁悬浮电动机的电磁力特性研究［J］.组合机床与自动化加工技术，2010(8):27-29.

【3】宁建荣，夏加宽，沈丽，等.PMLSM直接驱动工作台的机电耦合有限元建模［J］.沈阳工业大学学报，2011，33 (6):618-622.

【4】孙宜标，王欢，杨俊友.H∞最优控制的PMLSM伺服系统鲁棒重复控制［J］.沈阳工业大学学报，2012，34(3): 241-246.

【5】陶永华.新型PID控制及其应用［M］.北京:机械工业出版社，2002.

【6】吴振顺，姚建均，岳东海.模糊自整定PID控制器的设计及其应用［J］.哈尔滨工业大学学报，2004，36(11): 1578-1580.

【7】孙华，张涛.永磁同步直线电机的模糊PID控制及仿真试验［J］.机床与液压，2011，39(5):108-110.

【8】刘绍鼎，樊立萍，姜长洪.基于模糊规则参数自整定PID控制器的设计［J］.微计算机信息，2007，23(10):50-52.