跨文化视角下的中国数学教育特点探析——到底什么是中国式的数学教学

孟令奇，张德利

（1.曲阜师范大学 教育科学学院，山东 曲阜 273165；2.吉林省教育学院，吉林 长春 130022）

近年来，越来越多的学者（例如：张奠宙，刘兼，康世刚，郑毓信）开始关注“中国数学教育特点”问题[1～4].从某种程度上说，廓清这个问题是研究数学教育本土化的前提.中国学者们（例如：于伟，秦玉友，2009）已经开始探讨教育本土化的重要性[5].课程改革需要有“本土化”作为支撑.因此，“中国数学教育特点”争鸣的研究称得上是数学教育研究的重要问题.张奠宙（2010）认为中国的数学教育可以总结为一个“双基+变式+思想方法”的一个立体图[1].并认为中国数学教育的特色主要表现为：（1）注入“导入”环节；（2）尝试教学；（3）师生互动；（4）解题变式演练；（5）提炼“数学思想方法”；（6）解读“熟能生巧”.刘兼（2010）从“双基”提法的由来出发，不赞同“双基”为中国数学教育特色，并引用吴文俊的观点，认为以《九章》为代表的传统数学内容或称东方数学所蕴含的思想方法才可称得为特色[2].郑毓信在综合了张奠宙和刘兼的观点之后，提出了自己的观点，认为应该区别中国数学传统和传统的数学教育，同时认为学者们应该“围绕数学教育的基本问题，也即数学教学方法、数学教学思想与数学教育思想等对中国数学教育传统做出梳理”[4].康世刚则首先讨论了“传统”的概念，并给出界定的标准，由此得到中国数学教育的优良传统是：（1）“双基”教学；（2）熟能生巧；（3）变式教学；（4）精讲多练、解题教学及“三大”能力培养等[3].那么到底谁的论述正确呢？将这个问题置于跨文化比较心理学的视角之下并探讨上述数学教育特征是否真正反应了中国式教学的本质.反思中国数学教育的自身特点隐含着一个潜在的命题，即中国数学教育和西方数学教育的比较问题[6].从一个广阔的视角来看，属于中西方比较教育的问题.而在近年来的国际比较教育研究中，越来越多的学者（例如：Thomas，1997；Phillips和 Schweisfurth，2006；Phuong，Terlouw和Pilot，2006）开始意识到在比较教育研究中本土文化的影响是本质的[7～9].Phillips和Schweisfurth做过比喻，盲目地学习外国的教育经验就如同随意地从外面的公园中采集鲜花种植在自己家的花园中而忽略了土壤的不同性.研究这个问题对数学课程改革有重要的意义.事实上，无论提及“本土化”或“传统”，都是和“文化”一词分不开的.而在过去的几十年中在跨文化心理学中关于文化的本质的研究并没有一致性的结论.首先回顾过去50年来跨文化心理学中几种比较流行的文化观及其争论，然后透过文化的视域反思如上提及的中国数学教育特点的合理性并提出研究展望.

1 当前跨文化心理学中比较公认的东方文化观及其争论

作为最有争议的一个词汇，“文化”在1952年之前便有164种以上的不同定义（Kroeber和Kluckhohn，1952）.后来被延伸到 250种之多[10].这些定义与研究来自于不同的学科，服务于不同的研究目的.就方法论而然，近年来文化的定量研究在跨文化心理学中占很大的比重，其中绝大多数定量文章集中在对工具以及其信度效度的研究.文化的定性研究，特别是针对文化本身的研究和定量研究相比显得薄弱.这里主要介绍和教育有关的3种代表性的文化观，儒家传承文化观、集体主义文化观和维度文化观，以及它们对研究数学教育本土化的作用.

1.1 儒家传承文化观

儒家传承文化观（CHC, Confucian Heritage Culture）是近年来经常用到的解释东方教学与学习特征的一个常用模型[11～13].尽管关于儒家文化的定量模型在20年前已有研究，但近年来当人们探讨儒家传承文化对教学的影响时并不是应用一个定量的工具进行测量.比较教育的学者们更多的是采纳一个非常不严格的定义来阐述文化与教学的关系.在中国，儒家文化多指以孔子为代表的文化思想.但在国际比较教育中儒家传承文化观已被泛指为儒释道的一个大杂烩.另外，儒家传承文化观已经“走出国门”，它更多的是指受儒家思想熏陶和影响的国家（或地区）的文化包括日本、韩国、马来西亚、新加坡等国和中国的港台地区.在过去的10年中，儒家传承文化观已成为东方文化的代名词.关于这种文化如何影响教学和学习，读者可阅读《华人如何学数学》（范良火，王乃英，蔡金法，等，2004）.此书用大量的篇幅来阐述儒家传承文化观与中国数学教学及学习的关系.例如，该书第十七章介绍了一个基于孔子教育思想的教学模型，第五章、第十九章专门阐述中国文化问题.作者们传递给读者的重要信息是：（1）中国大学生的学习观仍然反映了中国传统的学习文化观，特别是孔子的学习观；（2）中国当代的数学教学与学习，反映了儒家文化传承下的学习现象.尤其是儒家传承文化观在第十九章的解释中进一步扩展为具有反映儒释道3种价值观的谚语或古代圣哲（孔子、朱熹、六祖慧能等）的学习或教学观.例如，下面的谚语或古代圣哲观点被认为深刻影响了当代数学学习和教学：熟能生巧；勤能补拙；不悱不启，不愤不发；温故而知新；求其似，求其不似等.这本书的其它章节也具有用儒家或道家的思想去解释中国数学教育的倾向.总而言之，此书向数学教育界传递了两个非常重要的信息.第一，在当前市场经济为主导的中国，中国传统的学习文化观仍然反映在中国人的头脑中；第二，儒家文化传承可以作为中国传统文化的代表.

1.2 集体主义文化观

集体主义文化观（Collectivism）是跨文化心理学的热门话题之一.它常常和个人主义文化观（Individualism）加以比较.在很多定量研究中，这两个问题常常放在一起来建构同一工具.例如，针对测量工具中的同一问题，被试者要选择“1，2，3，4，5”中的一个数字来确定其对这一问题的认可程度.如果选1代表一种集体主义文化倾向的化，那么选5便代表一种个人主义文化倾向.奥瑟曼、库恩以及克麦米亚（Oyserman，Coon和Kemmelmeier）在2002年总结了这一领域的主要研究[14]成果，他们发现关于集体主义文化观主要有4类研究：自我概念、关系论、归因理论和幸福感.在每一类中又详细列出了主要问题.例如，关于自我概念，集体主义文化观倾向于团体的利益要高于个人利益.值得称赞的个人特征是能够反应集体精神的目标，例如为集体而牺牲个人利益，和其他成员有着和谐的人际关系等.关于关系论，奥瑟曼、库恩以及克麦米亚则总结了两类，重要的成员关系是固定的，另一类则是人际关系圈的稳定性.集体主义和个人主义的文化观通常被看成是东西方文化的代名词.这两种文化观是比较教育学者解释东西方不同的教育现象的重要文化模型.

1.3 维度文化观

关于文化维度（Cultural dimensions）的研究是过去30年来跨文化比较心理学的热点问题.如上所述，文化的定义庞多而繁杂，维度说是其中的定义之一[15].霍夫斯塔德（Hofstede）在1980和1991分别提出了文化的四维度理论和五维度理论.霍夫斯塔德的研究方法主要是定量方法.其样本是IBM的116 000名分布于40个国家的员工.维度文化观的一个基本假设是维度作为基本的文化要素普遍存在于人们的头脑中.但作为不同的地域可能对同一维度有不同的认识倾向.尽管这种提法并不是专门用来研究东方文化的，但维度文化研究者通常将维度视为研究任何文化地域的普适性工具，所以同样适于解析东方文化.霍夫斯塔德1980年提出的四维度文化观是：权力差距（Power Distance）、不确定性规避（Uncertainty Avoidance）、个人主义（Individualism）以及男性化（Masculinity）.权力差距被定义为人与人之间的平等程度.不确定性规避则指对于不确定和模糊情景的容忍程度.个人主义则主要指个人和集体的关系：一个个人主义为主导的社会的人际关系是松弛的——个人考虑的主要问题是从自己而不是从家庭、团体和社会.男性化倾向是指性别在社会角色中的作用.尽管绝大多少研究集中在用定量的方法来测试或验证工具，但仍看到少数研究直接应用霍夫斯塔德的方法在教育上进行研究.例如沃克和戴马克（Walker和Dimmock）在1999年将霍夫斯塔德的四维度理论拓展为六维度，主要对象是对教育管理的文化影响研究而不是像霍夫斯塔德那样针对商业和经济机构的研究.同时也发现国内外的学者直接应用霍夫斯塔德的四维度或五维度模型来解释教育现象，甚至课堂教学模式.

2 三种文化观述评及关于文化观问题的争鸣

在如上提及的3种文化观中，儒家传承文化观是在数学比较教育中经常被采用的的模型，其它的两种则应用较少.倾向于儒家传承文化观的一个原因可能是这种文化观更容易和学习与教学相联系.一个简单的例子是孔子的论语是一个非常典范的传统学习和教学的范例.当人们反思中国式数学教学时，很容易将现行的教学模式和古代的学习传统相结合.另一个原因可能是另外两个模型偏向于定量研究，而数学教育中的很多教学问题难与另外两种模型相契合.事实上，应用定量研究虽然有一定的局限性，但从文化的变化的角度来看，定量研究同样有一定的优点.因为它可以通过变量之间的相关性来揭示变化关系.同时也可以通过对同一样本的不同时间的测试来揭示变化程度.这一点是儒家传承文化观所缺失的.但这并不是说研究者发现了“新大陆”，只要将数学教育问题和另外两种文化观相结合，就可以解决用传统文化来解析数学教学的问题.3种文化观本身的局限性限制了研究者将文化和教学相结合的愿望.文章开始提出的争鸣问题很多来自与对文化本身的认识，而不是仅仅涉及数学教育现象.下面简述两个和教学有关的关于文化的争鸣并希望由此启发人们深入思考关于中国数学教育特点的争鸣.

第一个文化争鸣问题是文化和地域的关系.很多比较教育学者在探讨儒家传承文化观和维度文化观中质疑这个问题.王乃英（2004）指出：“我们怀疑香港是否被分为儒家文化传承由于其西方文化的影响……中国大陆有28个省份和56个民族.在地理位置上很难界定中国的中心……”[13]在1998年的数学教育亚洲会议上，一位新加坡的学者拒绝将新加坡界定为儒家传承文化圈.这个问题到目前为止文化学者们鲜有给出一个较为合理的解释.一个平行的问题可以在数学教育中提出：中国数学教育特点到底指的是什么？是抽象的和传统文化相连结的概念，还是各个地区中地区的课改实验典型的集合？在文章开始提及的张奠宙、康世刚等提出的6个特点中，至少有3个是来自课改实验的研究.如果各个地域的教改实验能够代表中国式教学，接下来的问题是筛选这些教改实验的标准是什么.这些教改实验在多大程度上反映了中国传统文化？

第二个文化争鸣问题是文化抽象程度问题.即到底将文化抽象成一个单一的“脚本”（script）还是多个不同的特征.王乃英在2004年总结了一个CHC script，即一个具有文化儒家传承文化特征的教学模型（如图1）.

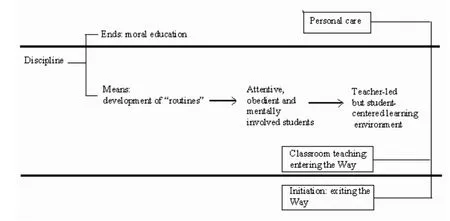
图1 教学模型

在这个模型中，discipline指的是学科，它可以是数学、语文或其它学科.接下来的两个延伸部分是终极目标和实施手段.终极目标被定义为道德教育（这一目标的确定可能根据孔子的教育思想）.实施手段则表述为“常规”的发展，即在一个课堂中教师确定“什么时候讲，什么时候给学生课堂练习，什么时候让学生打开书本，什么时候让学生看板书或计算机投影等”[13].这些常规的教学所针对的是注意力集中的、服从教师的并积极思考的学生.所产生的教学应该是教师主导的同时学生为中心的学习环境.最下边的两项“entering the way”指的是教师将指导学生获得基本知识.“exiting the way”指的是在个别辅导后寻求相同中的不同性.

鲁湃兹等学者（LOPEZ-REAL，MOK Ah，LEUNG，MARTON）在2004年则提出过度抽象的不合理性[16].他们在研究了同一教师的连续教案并指出寻求一个普适性的“文化脚本”（cultural script）是很难的.教师在实际教学中总是变化其教学设计.他们倾向于用教师的“教学模式”（a“pattern of teaching”）来描述教学.他们将一个教师的教学模式定义为，可识别的教师教学实践特征，这种特征会在一定的时期内重复出现.这一特征可以标志这个教师的教学风格.

在文化维度观和集体主义文化观研究中同样可以看到关于对文化抽象程度的讨论（例如McSweeney，2002）[17].但讨论的焦点并不和教学问题有多大的联系.和教学问题联系较多的是在儒家传承文化观中的讨论.类似的问题同样反映在中国数学教育特点的争鸣中.例如，张奠宙在2010年的文章开篇便提出了可以用一句话来概括中国数学教育的特色，即“在良好的数学基础上谋求学生的数学发展”[1].一个和文化争鸣类似的问题可以在这里提出：中国数学教育特色到底是一个还是多个？

3 跨文化视角下的中国数学教育特点的反思

如前所述，很多中国数学教育特点的争鸣问题从本质上来说是源于文化的争鸣.而很多在文化上的争鸣问题并不是在短期内能够解决的.所以文章的目的是从一个小的侧面去分析文章开始时提及的中国数学教育特点.这种分析所注重的是“解释的合理性”而不是“解释的正确性”.即如果从假设的前提出发来审视是否一些被解释为中国数学教育特点的合理性——并不是说他们的提法是错误的或是正确的.在下面的分析中，主要考虑儒家文化传承的历史观和独特性.历史观作为一个重要的文化解析的手段早在60年前便被多数文化学者所认可.研究者同样认为文化的独特性非常重要.

3.1 关于启发式教学和熟能生巧及变式教学

从儒家文化传承的视角来审视学者们对中国数学教育特点的总结，研究者认为“启发式教学”、“熟能生巧”和“变式教学”有着深厚的本土文化含义.很多其它的流行说法包括突出“双基”并不能真正地给出一个合理的文化解释，或即便给出一个文化解释，也难以找到和西方数学教育的本质不同性.例如，就本质而言，启发式教学的思想始于孔子的“不悱不启，不愤不发”（第五红艳，2004；韩龙淑，2008；寇敏娟，2009）[18～20].在某种程度上反映了“痛”学思想，和西方的“乐”学思想有本质差别.从杜威的儿童中心论到纳丁（Noddings，1984）的关爱理论[21]，西方哲学家在某种程度上有“乐”学教育倾向.目前在西方的建构主义思潮影响下的课程改革也凸显了“乐”学的思想.同样的，关于“熟”与“巧”的关系，西方学者和东方学者有着根本性的分歧，有兴趣的读者可以阅读有关西方学者关于东方教育中的机械训练的文章.变式教学的本土文化根源是妇幼皆知的，体现在作为群经之首的《易经》和道家阴阳学说中.从历史的角度看，教中求变是中国教师潜意识的文化积淀.数学变式教学的提倡者之一顾泠沅曾是青浦县的教研员，其文化底蕴和实践经验非常丰厚.其令人折服的青浦教改实验无疑受到中国传统文化的深刻影响.相反的，“变式”在西方文化中并非主流，虽然在美国过去流行的一套中学数学教科书（作者Saxon）中在某种程度上体现了变式训练的思想，但并不被美国数学教师联合会所欣赏和接纳.

3.2 关于双基教学

对于强调“双基”的学习，研究者认为它不能成为区别于西方数学教育特征的中国特色.首先，“双基”没有强有力的本土文化根源作支撑.在有影响的古代圣哲或学习原理中，很难找到把“双基”作为首位的论述.其次，强调“双基”是中美共同关心的课程话题，或广而言之，是一个全球共同关心的话题，并非中国独有.相反的，“双基”教学在美国倒有着深刻的文化根源.从19世纪初到20世纪60年代，行为主义学者在说服教育工作者应用“刺激—反应”理论在学校教学中时，基础知识与基本技能已是其重要目标（尽管提法不同）.技能的习得是行为主义教学的主要目标.而技能的习得是通过对基础知识的反复强化而实现的.再次，美国2000年的课程标准，2006年的课程焦点都把基础知识与基本技能作为学生学习的重要目标[22～23].在美国2000年的课程标准第84页，对于Pre K-2年级的学生提出了明确的有关基础知识和基本技能的建议.不但要求对数的理解（understanding），同时也要求熟练（fluency）数的基本加减.美国2000年的课程标准中也经常引用教育研究文献来阐述基本知识与基本技能的重要性.例如，Bransford、Brown 和 Cocking（1999），Hiebert，Stigler，Jacobs等（2005），Thornton（1990），Hiebert（1999），Kamii，Lewis，和 Livingston（1993），Hiebert和 Lingquist（1990）的有关技能与基础的研究都被列为有说服力的证据.特别是第 35页的陈述和中国的“双基”提法十分相近.另外，在美国2006年的课程焦点第13和14页中，明确提出儿童不但要理解加减法的计算策略，同时还要有能力快速地回想加减法的基本法则.如果分析一下美国各州的课程的话，基础知识和基本技能更是其重要的课程目标.例如，路易斯安娜州的综合课程，明确强调GLEs（grade level expectations）[24].尽管美国各州对GLEs的要求不尽一致，毋庸讳然，GLEs本身就是对基础知识和基本技能的一个明确要求，这里不再多述.

3.3 关于尝试教学

尝试教学是否为中国特色之一，研究者认为亦需要探讨.即使承认尝试教学可以追朔为中国先哲们的教育理念（邱学华，1998）[25]，尝试法似乎在西方的文化底蕴和流行程度远高于东方.西方自然科学家和发明家们（如阿基米德、亚里士多德、加利略、居里夫人、爱迪生、孟德尔等）早已把尝试作为一种信手拈来的方法运用在其科学研究和发明中.近年来教育心理学家们所讨论的研究性学习、发现学习和以问题为中心的学习，均具有明显的尝试痕迹.而在以美国2000课程标准的理念为指导的课程设计中，尝试同样是非常重要的.在中国，尝试的理念受到外来影响是毋庸置疑的.G·波利亚的数学教育著作曾经在中国20世纪80年代风靡一时，其提倡的合情推理及数学发现具有尝试的特征.同样不能否认，深受波利亚教育思想影响的 MM 教育方式[26～28]，有着很强的尝试倾向.例如，其两条基本原则（既教证明又教猜想的原则和教学、学习、研究发现同步协调原则）彰显了猜想和发现的重要性.如果提倡猜想和发现，那么尝试的方法就是不言而喻的.至于顾泠沅的1980年的教改实验，研究者认为似乎更多应该归属于变式教学之列.这可以在其后来的文章中找到证据.研究者同时认为，尝试教学的理念在中国30年来的发展并不是显示了其本土性，而是显示了中国文化的包容性.

4 研究展望

从本土文化的角度来解析中国数学教育的特点是呈现在学者面前的一项重要而艰巨的任务.说它重要，是因为此问题触及了跨文化比较心理学的核心议题之一.说它艰巨，是因为当前的跨文化比较心理学研究还没有给数学教育工作者提供强有力的文化工具.近年来，在国际比较教育论坛中关于对文化和本土文化的诠释和解析并没有一个一致性的结论.由于比较教育学者过多地注重用儒家传承文化观来研究中国式教学，关于文化的变化以及文化的相互影响问题并没有在过去的比较数学教育中得以充分阐述.维度文化观和集体主义文化观在这方面能提供一些借鉴.基于对文化的理解以及当前中国数学教育特点的研究现状，如下问题值得数学教育工作者进一步探索.

第一，理论一致性问题.如前所述，如果从文化的角度来阐述中国数学教育特点，应该明确所应用的是一种什么样的文化观，在一个所选的文化观中，又侧重了哪个方面.这样可以保证前后论证地一致性.在上面的论述中，如果选择文化的维度论，可以阐述双基教学是中国数学教育特征.但如果考虑到儒家文化的独特性，双基教学则很难被解析为中国数学教育特征.

第二，层次性问题.尽管在文化观的研究中关于文化抽象度有很多争论，在对中国数学教育特点的研究中，对层次的划分非常必要.如果仔细分析以前的分类，不难发现先前的讨论并没有想到层次性问题.例如，注入“导入”环节只是一个课堂教学中的小片段；尝试教学则是一个教改实验；师生互动是一种教学方式；熟能生巧则是一种中国古代学习观.而双基教学和三大能力培养则直接来源于教学大纲或课程标准.郑毓信在反思张奠宙和刘兼的观点时，提出应该区别“中国数学传统和传统的数学教育”已经考虑了研究层次性问题.在这里呼吁这个问题需要进一步细化.

第三，动态性问题.绝大多数文化学者同意文化是个动态的过程.课程改革的背后有着中西方文化的交融的过程.在研究中国数学教育特点时，应该进一步廓清传统的教学与新的教学之间的关系.目前的研究中很少区别中国文化独有的教学特征和中外结合的教学特征这种动态的问题.动态性问题还包括如何看待中国的教育传统和当前的市场经济环境的关系.如何将教学置于大的社会经济背景之下进行考虑等.如何看待应试教育对数学教学的影响等.如前所述，维度文化观和集体主义文化观可以给教育工作者提供一些研究变化的方法.但具体如何应用还是一个难题.

第四，实证性问题.目前关于中国数学教育特点的实证性研究不多.实证研究是克服争鸣，积累数据，验证假设的最好方式之一.

第五，实践性问题.过去很多被总结的中国式教学来自于教改实验或课堂教学.而这些经验性结果多来自各级教研机构数学教研室和广大一线教师.在这一问题的今后研究中，这些实践者将会继续起非常重要的作用.如何能够总结出经得起推敲的本土教学经验是摆在所有实践者面前的难题.研究者呼吁理论研究者应该和实践者密切结合，取长补短，只有这样，才能使这一领域的研究走向成熟.

[1] 张奠宙.关于中国数学教育的特色——与国际上相应概念的对照[J].人民教育，2010，（2）：40-42.

[2] 刘兼.“重视双基”能成为我们的优良传统吗[J].人民教育，2010，（2）：39.

[3] 康世刚.也谈我国数学教育的优良传统[J].人民教育，2010，（2）：40.

[4] 郑毓信.关注现实，加强比较，聚焦基本问题，也谈中国数学教育传统[J].人民教育，2010，（6）：39.

[5] 于伟，秦玉友.本土问题意识与教育理论本土化[J].教育研究，2009，（6）：27-31.

[6] Ma L. Knowing and Teaching Elementary Mathematics: Teachers’ Understanding of Fundamental Mathematics in China and the United States [M]. Mahwah, NJ: Lawrence Erlbaum Associates, 1999.

[7] Thomas E. Developing a Culture-sensitive Pedagogy: Tackling a Problem of Melding “Global Culture” within Existing Cultural Context [J]. International Journal of Educational Development, 1997, 17(1): 13-26.

[8] Phillips D, Schweisfurth M. Comparative and International Education [M]. London: Continuum International Publishing Group, 2006.

[9] Phuong M N, Terlouw C, Pilot A. Culturally Appropriate Pedagogy: the Case of Group Learning in a Confucian Heritage Culture Context [J]. International Education, 2006, 17(1): 1-19.

[10] Kroeber A L, Kluckhohn C. Culture: a Critical Review of Concepts and Definitions [M]. New York: Vintage Books,1963.

[11] Fan L, Wong N, Cai J, et al. How Chinese Learn Mathematics: Perspectives from Insiders [M]. Singapore: World Scientific Publishing Co. Pte. Ltd, 2004.

[12] An S. The Middle Path in Math Instruction: Solutions for Improving Math Education [M]. Lanham, MA: Scarecrow Education, 2004.

[13] Wong N. The CHC Learner’s Phenomenon: Its Implications on Mathematics Education [A]. In: Fan L, Wong N, Cai J, et al. How Chinese Learn Mathematics [A]. Singapore: World Scientific Publishing Co. Pte. Ltd, 2004.

[14] Oyserman D, Coon M H, Kemmelmeier M. Rethinking Individualism and Collectivism: Evaluation of Theoretical Assumptions and Meta-analyses [J]. Psychological Bulletin, 2002, 128(1): 3-72.

[15] Hofstede G H. Cultures Consequences: International Differences in Work-related Values [M]. Beverly Hills, CA: Sage,1980.

[16] Lopez-real F, Mok A C I, Leung K S F, et al. Identifying a Pattern of Teaching: an Analysis of a Shanghai Teacher’s Lessons [A]. In: Fan L, Wong N, Cai J, et al. How Chinese Learn Mathematics [C]. Singapore: World Scientific Publishing Co. Pte. Ltd, 2004.

[17] McSweeney B. Hofstede’s Model of National Cultural Differences and Their Consequences: a Triumph of Faith—a Failure of Analysis [J]. Human Relations, 2002, (55): 89-118.

[18] 寇敏娟.论孔子的启发式教学[J].太原大学教育学院学报，2009，（27）：4.

[19] 韩龙淑.数学启发式教学研究评述[J].教学与管理，2008，（11）：52.

[20] 第五红艳.我国启发式教学的回顾与前瞻[J].陕西师范大学继续教育学报，2004，（21）：225.

[21] Noddings N. Caring: a Feminine Approach to Ethic & Moral Education [M]. Berkeley: University of California Press,1984.

[22] National Council of Teachers of Mathematics (NCTM). Principles and Standards for School Mathematics [M]. Reston,VA: The National Council of Teachers of Mathematics, Inc, 2000.

[23] National Council of Teachers of Mathematics (NCTM). Curriculum Focal Points for Prekindergarten through Grade 8 Mathematics [M]. Reston, VA: The National Council of Teachers of Mathematics, Inc, 2006.

[24] Comprehensive Curriculum: Retrieved [DB/OL]. http://www.doe.state.la.us/lde/saa/2108.html

[25] 邱学华.尝试教学思想的历史渊源[J].山东教育科研，1998，（3）：13.

[26] 运怀立，杨之.MM教育方式与当代数学教育[J].数学教育学报，2005，14（4）：74-75.

[27] 魏立平，马晓燕，朱殿利.谈数学教师专业化培养的改革——“MM（HT）教育方式”的启示[J].数学教育学报，2006，15（2）：97-99.

[28] 林夏水.从MM教育方式到TEC教学方式[J].数学教育学报，2007，16（1）：1-3.