题目难度和冗余信息对代数应用题信息区分策略影响的实验研究

岳宝霞，苏 颖，冯 虹

（1.天津师范大学 教师教育学院，天津 300387；2.天津市耀华中学，天津 300040；3.天津师范大学 教育科学学院，天津 300387）

1 问题提出

应用题是应用数学问题的简称，也称为文字题（word problem），是用自然语言表达的数学问题，需要解题者将自然语言文字转化为“数学符号构成的算式”，然后用数学方法求解.

已有研究表明，小学加减应用题的难度对学生解题影响显著[1～3].Decorte等人的研究表明，题目语义结构对不同学业程度解题者的解题过程会产生影响[4].早期研究表明，当题目中含有冗余信息时，解题者区分相关和无关信息更加困难[5～6].所谓冗余信息即题目中含有的多余条件或无关信息，通常情况下，题目中的信息均为解题必要信息，如果在题目中插入冗余信息便会增加题目的难度.尽管研究表明，插入无关信息通常导致解题错误，但没有指出儿童区分信息并形成有用表征的过程是怎样的[7].

分析已有文献发现，以往的研究大多强调解应用题过程的内在表征，很少关注解题者使用了怎样的信息区分策略来区分有用的和无关的信息[7].信息区分策略指学生在解题过程中将题目背景及问题分析成语义单元，对信息类型进行检验、区分，找出信息之间的相关性，目的是对这些信息进行比较进而与题目中的问题相匹配.对参与实验的学生的眼动轨迹进行分析发现，学生共使用了5种区分策略：重读题目策略，单一比较策略，以特征为基础策略，问题—引导策略和首次读题区分策略.

已有研究中实验材料多为算数应用题，极少涉及代数应用题.曾有研究发现，初中生从研究具体数字到学习用字母表示数和未知元，会出现认知上的困难[8].因为算术在很大程度上是过程性的，所以学生习惯于思考用于解决问题的运算，而不是思考应该用来表征问题情境之间关系的运算.因此，研究代数应用题解题过程具有实践意义.在研究方法上，Littlefield等人使用了计算机软件辅助、口语报告等方法，均有其局限性[7，9～10].研究将以初二年级学生为实验对象，对不同数学成绩学生使用的信息区分策略进行分析.在实验方法上，采用眼动分析技术，考察学生在题目自然呈现的条件下对几种信息区分策略的使用情况[11～20].

2 方 法

2.1 被 试

对学生数学成绩的高、低分组按照以下标准进行：

（1）以初一数学成绩的学年总评和初二的第一次数学统考成绩为指标，年级前15%的学生为数学成绩高分组的候选人，居于年级后15%的学生为数学成绩低分组的候选人.

（2）教师评定，班主任和数学教师根据候选学生的平时表现，对他们进行高分组和低分组的划分.最终在初中二年级选择数学成绩高分组和低分组被试各16名，共32名被试，平均年龄为14±0.98岁.所有被试的智力、视力均正常.为了避免两组被试阅读理解能力的差异对题目理解的影响，对两组被试初二的第一次语文统考成绩进行了检验，结果表明，数学成绩高分组与低分组学生的语文成绩不具有显著差异.

2.2 实验材料

实验前先用30道题目对不参加实验的初中二年级两个班的学生进行测试（其中一半题目不含冗余信息，一半题目包含冗余信息），要求他们解题后对题目的难度进行两个等级的评定，即较容易、较难.然后请中学数学教师做相同项目的评定.将学生与教师的评定结果进行比较，从评定结果一致的4种类型题目中各随机抽取两道题，构成实验材料.

实验材料包括练习材料和正式实验材料.练习材料是与正式实验材料长度一致的较简单代数应用题.题目内容以初中二年级水平数学教材为基础，题目长度大致相同.正式实验材料共包括8道代数应用题.分为4种类型：较易的不含冗余信息的题目，较易的含有冗余信息的题目；较难的不含冗余信息的题目，较难的含有冗余信息的题目.

2.3 实验设计

采用2（数学成绩）×2（题目难度水平）×2（冗余信息：含、不含）的3因素混合实验设计.数学成绩为被试间因素，题目难度与冗余信息为被试内因素.

2.4 实验仪器

研究使用了Tobbi120型眼动仪.

2.5 实验程序

整个实验在实验室里进行.被试坐在显示器正前方，眼睛距离屏幕中心60 cm.实验有两名主试，一名负责操作眼动仪，另一名负责用录音笔记录被试的口语报告.实验指导语如下：同学你好，今天请你来做一个实验，目的是了解你怎样做题.做好解题准备后请按鼠标，屏幕上会出现一道应用题，你只需列出算式，不用计算结果.一旦你觉得能够列出算式，请立即按下鼠标，然后口头报告出算式并说出你的解题思路.如果你不会解这道题，也请你按下鼠标，继续进行下一题.开始实验前，主试先进行示范，并要求被试对练习材料报告解题计划.在确认被试明白指导语的要求后，开始正式实验.

2.6 眼动记录指标

眼动仪记录以下指标作为因变量：

（1）眼动轨迹：解题者对题目注视的全部眼动过程，包括眼跳、回视及注视点在某处停留时间等.为考察学生采用的信息区分策略，在Littlefield等人工作的基础上对5种策略进行分析，并分析每个学生的眼动轨迹，最后由专家和中学教师评定.

① 重读题目（rereading）策略：通过重复地阅读题目，将部分信息及语义特征贮存到工作记忆中，然后对信息进行比较，使用“重读题目”策略的被试，可能是整篇重读也可能是整句重读，但不管怎样回视次数会很多.

② 单一比较（simple comparison）策略：使用单一比较策略的被试在数字及关系词之间进行简单直接的比较，解题者可能会根据问题部分的要求直接列出方程.

③ 以特征为基础（featurally-based）策略：在题目中寻找与问题中的语义相匹配的语义特征，通常会将注视点集中在变量名或与问题部分相似的事件、概念上，如：速度、长度、工程施工等.

④ 问题—引导（question-guided）策略：以问题中的语义词语为指导，对信息进行分析，使用“问题引导”策略的被试，注视点经常回到问题区域.

⑤ 首次读题（discriminate during initial reading）区分策略：首次读题后就对语义类型进行了区分，找到解题所需的关键信息，注视点集中在关键信息和相关数字信息上，如：“…的速度比…的速度快…”，“比原计划提前*天”等；且总注视次数显著少于其他的策略.

（2）注视点出入次数：指被试在某个兴趣区的注视点出入的次数.

兴趣区的划分：实验将含有冗余信息的题目划分为 7个兴趣区，即题目、相关数字、无关数字、相关事件及行为、无关事件及行为、关键信息、问题（较易题目含有一个无关数字，较难题目含有两个无关数字）；将不含冗余信息的题目划分为5个兴趣区，即题目、相关数字，相关事件及行为、关键信息、问题（较易题目含有2～3个相关数字，较难题目含有4个相关数字）.其中相关数字指在问题表述中对计算正确答案必需的数字；无关数字指在题目表述中出现的，对计算正确答案无用的数字.

2.7 实验结果的统计

采用SPSS for Windows 16.0统计包进行处理.

3 结果分析

3.1 题目难度和冗余信息对不同成绩学生信息区分策略的影响

根据学生的眼动轨迹，分析被试解题过程中采用的信息区分策略，并记录下不同成绩学生解不同类型题目时采用的一种或几种信息区分策略，每种信息区分策略使用频率见表1.

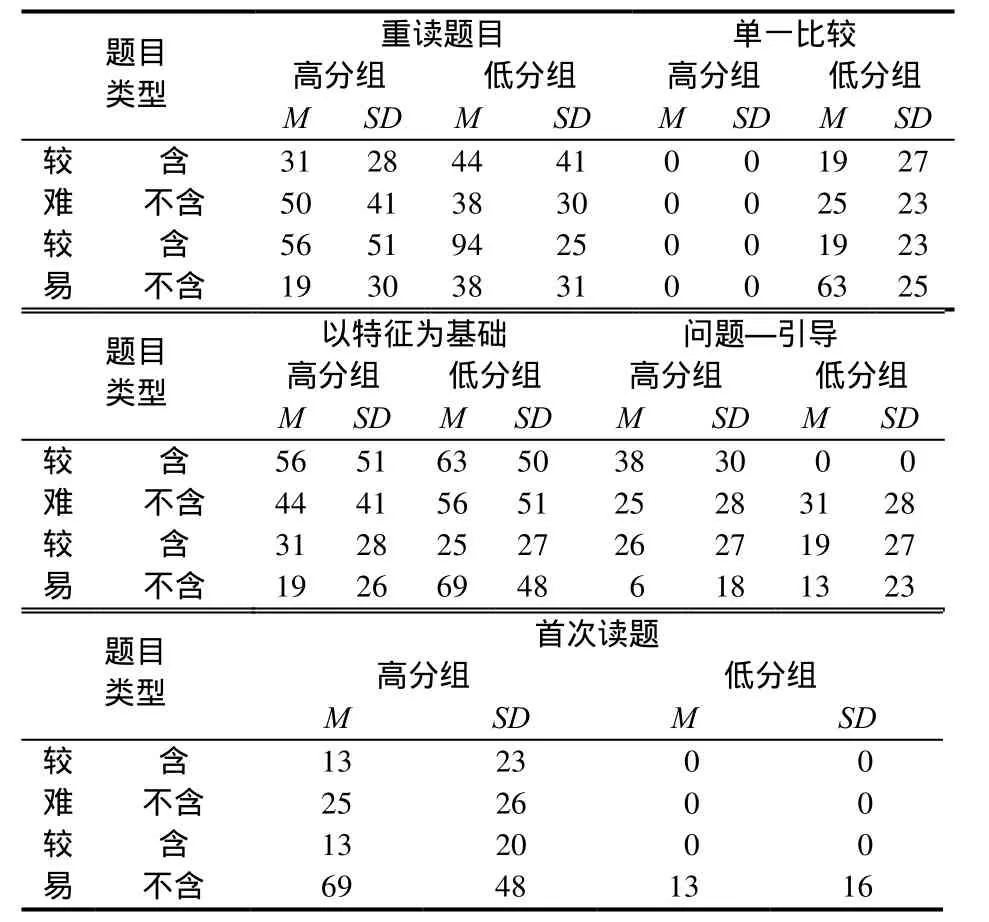
表1 不同成绩学生解不同类型题目时采用的信息区分策略百分比（%）

对不同成绩学生解题时信息区分策略使用频率进行重复测量方差分析，结果如下.

（1）重读题目策略：冗余信息的主效应显著F(1,30)=7.848，p=0.009，即题目含有冗余信息时解题者使用重读策略的频率显著高于不含冗余信息题目.题目难度和冗余信息的交互作用显著F(1, 30)=12.350，p=0.001.简单效应分析结果显示：对于较难题目，无论是否含有冗余信息，解题者使用重读策略频率的差异不显著；对于较易题目，使用重读策略的频率在冗余信息间存在显著差异t(31)=4.676，p=0.000，即解含有冗余信息的易题时使用重读策略的次数多于解不含冗余信息的题目.

（2）单一比较策略：数学成绩的主效应显著F(1,30)=4.84，p=0.036，即低分组学生使用单一比较策略的频率显著高于高分组学生；题目难度和是否含有冗余信息的主效应不显著.3因素间的交互作用不显著.

（3）以特征为基础策略：数学成绩和冗余信息的主效应不显著，题目难度的主效应显著F(1, 30)=5.870，p=0.022，即被试解较难题目时使用该策略的频率显著高于较易题目.3因素间的交互作用不显著.

（4）问题—引导策略：数学成绩、题目难度和是否含有冗余信息的主效应均不显著.数学成绩和冗余信息的交互作用显著F冗余*成绩(1, 30)=6.106，p=0.019.简单效应分析结果显示：对于高分组学生，其使用问题—引导策略的频率在冗余信息间差异不显著；对于低分组学生，使用问题—引导策略的频率在冗余信息间存在显著差异t(31)=-2.236，p=0.041，即解不含冗余信息的题目时使用问题—引导策略的频率显著多于解含有冗余信息的题目.

（5）首次读题区分策略：数学成绩的主效应显著F(1,30)=33.092，p=0.000，即高分组学生使用首次读题策略的频率高于低分组学生；题目难度的主效应显著F(1, 30)=6.497，p=0.016；即被试解较易题时使用该策略的频率高于较难题；冗余信息的主效应不显著.数学成绩和冗余信息的交互作用显著F冗余*成绩(1, 30)=10.565，p=0.003.简单效应分析结果显示：对于高分组学生，使用首次读题区分策略的频率在冗余信息间存在显著差异t(31)=-4.568，p=0.01，即解不含冗余信息题目时使用首次读题策略的次数多于解含有冗余信息题目；对于低分组学生，该差异不显著.

3.2 题目难度和冗余信息对不同成绩学生出入“问题”区域次数的影响

研究记录了被试对题目中“问题”的注视次数及注视点移动轨迹，得到了被试出入“问题”区域次数，不同数学成绩学生解不同类型代数应用题时进出“问题”区域次数如表2.

对学生解题时进出“问题”区域次数进行重复测量方差分析，发现冗余信息主效应显著F(1, 30)=4.439，p=0.044，即学生解含有冗余信息题目时注视点进出“问题”区域的次数显著高于不含冗余信息题目.数学成绩和冗余信息的交互作用边缘显著F(1, 30)=3.456，p=0.073.简单效应分析显示：对于高分组学生，其注视点进出“问题”区域的次数在冗余信息上边缘显著t(15)=2.085，p=0.055，即当题目含有冗余信息时，学生进出“问题”区域的次数多于不含冗余信息的题目；对于低分组学生其差异不显著.

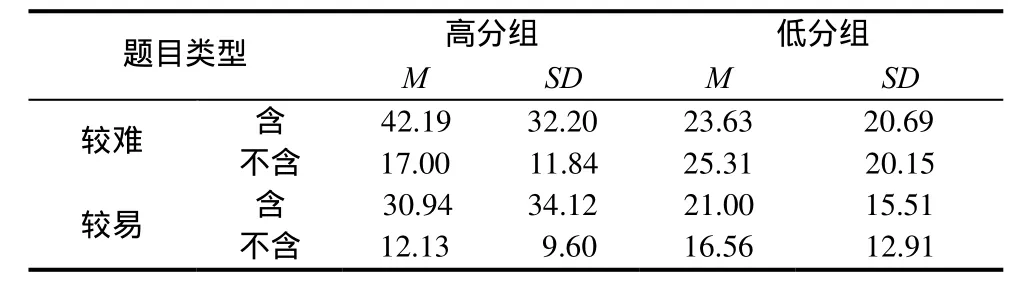
表2 不同数学成绩学生对不同类型题目进出“问题”区域的次数

3.3 题目难度和冗余信息对不同成绩学生表征“关键信息”的影响

研究记录了被试对题目中“关键信息”的注视点移动轨迹，得到了被试进出“关键信息”区域的次数，具体情况见表3.

对不同数学成绩学生进出“关键信息”区域的次数进行重复测量方差分析，结果表明：题目难度的主效应显著，F=9.105，p<0.005，冗余信息的主效应显著F=12.531，p<0.001，数学成绩、题目难度和冗余信息的交互作用边缘显著F=3.436，p=0.074.简单效应分析显示：无论题目难易，高分组学生进出“关键信息”区域的次数在冗余信息间都存在显著差异t较难=2.695，p<0.05，t较易=2.178，p<0.05；低分组学生解较易题时，进出“关键信息”区域的次数在冗余信息间存在显著差异t=2.046，p<0.05.

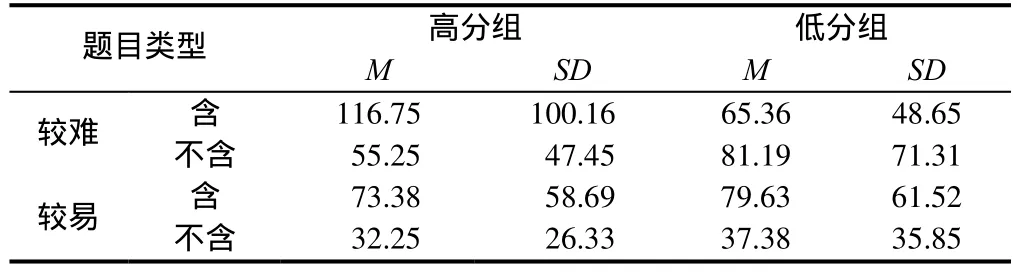
表3 不同成绩学生对不同类型题目进出“关键信息”区域的次数

4 讨 论

研究记录了不同成绩学生解不同类型题目时采用的一种或几种信息区分策略，对每种信息区分策略使用频率进行了统计，用来分析每种区分策略的使用受到哪些因素的影响.同时考察了被试在“问题”区域及“关键信息”区域注视点的进出次数，用来辅助说明被试对区分策略是否进行了调整.

4.1 几种信息区分策略的使用情况

重读题目策略使用频率较高，当题目较容易且含有冗余信息时，使用该策略的次数显著多于不含冗余信息的题目.说明对于易题，学生对冗余信息更加敏感，会因是否插入冗余信息调整该策略的使用.但当题目较难时，是否含有冗余信息对该策略的使用频率没有影响，原因可能是题目本身语意结构更加复杂，解题者需要使用多种信息区分策略从而降低了重读的使用频率.

高分组学生不使用单一比较策略，低分组学生在各种类型题目中都有使用，但使用的频率较低，且不受题目难度及冗余信息的影响.原因可能是使用该策略的低分组学生不会随题目类型的变化调整区分策略.

特征比较策略的使用频率也比较高，同时受题目难度的影响明显.即解难题时的使用次数多于易题，原因可能是当题目语义结构复杂时，解题者需要对题目中的情境信息进行更多的加工，如人物、变量、事件等.

对于问题—引导策略不同成绩学生都会使用，低分组学生在解不含冗余信息题目时使用该策略频率多于含冗余信息题目，但高分组学生不会因题目类型不同而对该策略的使用进行调整.

高分组学生在使用首次读题区分策略时会因题目类型不同进行调整，即解容易题时使用的次数多于难题，解不含冗余信息题目时使用次数多于含冗余信息题目.说明首次读题区分策略适用于语意结构较简单的题目，对于高分组学生来说题目中变量关系较为明显，首次读题后就能找到解题的关键要素.

4.2 题目难度和冗余信息对学生使用信息区分策略的影响

4.2.1 题目难度和冗余信息对低分组学生使用信息区分策略的影响

Littlefield研究认为，冗余信息可能会增加错误推理和情境中细节推断的错误率，或者会降低选择、整合有用信息的可能性.高分组会随题目难度变化调整区分策略，低分组则不作调整.研究的结果表明：

（1）由表3可知，当题目较容易时，含有冗余信息对低分组学生进出“关键信息”的次数会有影响.说明对于语义结构不太复杂的题目学生能够找出解题的关键要素，部分学生使用了首次读题区分策略.但当题目插入冗余信息时，低分组使用首次读题区分策略的比率为0.另外由表2知，无论题目难易含有冗余信息对低分组学生进出“问题”区域的次数都没有影响，表1显示低分组学生解含有冗余信息题目时，使用问题—引导策略的次数显著多于解不含冗余信息题目.原因可能是学生在解不含冗余信息题目时更多地使用了重读策略，因为两种策略的使用都会使得问题区域注视点出入次数增加.

（2）当题目较难时，是否含有冗余信息对低分组学生进出“问题”及“关键信息”区域的次数均无影响.这与表1中所示，低分组在问题—引导策略及首次读题区分策略的使用上不因题目是否含有冗余信息而存在差异的结果一致.说明当题目难度增大时，题目本身的语义结构更加复杂，低分组学生不会因题目类型不同而对信息区分策略进行调整.

4.2.2 题目难度和冗余信息对高分组学生使用信息区分策略的影响

实验结果表明，高分组学生对题目的难度及是否含有冗余信息更加敏感.

（1）无论题目是难还是易，冗余信息对高分组学生进出“问题”区域的次数都有影响.即当题目含有冗余信息时，高分组学生的注视点出入“问题”区域的次数显著多于不含冗余信息的题目.表1的结果显示，高分组学生不会因题目是否含有冗余信息而对问题—引导策略的使用进行调整，说明对于含有冗余信息的题目，高分组学生可能更多地使用了重读题目等策略.因为几种策略的使用都有可能使得“问题”区域注视点进出次数增加.

（2）无论题目是难还是易，高分组学生进出“关键信息”区域的次数在冗余信息间都存在显著差异.当题目含有冗余信息时，高分组学生进出“关键信息”的次数增多.这说明高分组学生对冗余信息更加敏感，当题目插入冗余信息时，他们会在冗余信息与解题的关键信息之间进行比较，通过对题目“关键信息”的分析区分有用和无用信息，从而导致该区域注视点出入次数的增加.

5 结论及教学建议

5.1 结 论

由以上的实验研究可以得到如下结论：不同成绩学生解题时会使用不同的信息区分策略，但高分组学生不使用单一比较策略，低分组学生则很少使用首次读题区分策略.低分组学生解较容易题目时会因题目是否含有冗余信息调整区分策略，但当题目难度增大时则不作调整；高分组学生会因题目难度及是否含有冗余信息调整区分策略.

5.2 教学建议

难题及含有冗余信息的题目增加了题目语意信息的复杂性，增加了问题表征的难度.低分组学生更容易受到影响，而高分组学生对语意信息更加敏感，对信息区分策略的使用更加灵活.在应用题解题教学的过程中教师可以有意识的加强信息区分策略的指导，比如：一道代数应用题中有哪些语意类型（事件、人物、变量、测量单位）的信息？如何找出它们之间的关系？与问题部分的语意信息以何种方式相关？等等.特别是对于低分组学生而言，加强对学生数学阅读理解能力的培养.指导学生分析语意信息之间的特征及关系，而不是将关注点只放在变量、数字及关键词上.

[1] Hegarty M, Mayer R E, Christopher A M. Comprehension of Arithmetic Word Problems: A Comparison of Successful and Unsuccessful Problem Solvers [J]. Journal of Educational Psychology, 1995, 87(1): 18.

[2] 陈英和，仲宁宁，田国胜，等.小学2～4年级儿童数学应用题表征策略差异的研究[J].心理发展与教育，2004，（4）：19-24.

[3] 冯虹，安蓉，阴国恩.比较应用题的问题表征研究[J].天津师范大学学报，2007，（4）：40-43.

[4] De Corte E, Verschaffel I, Pauwel A. Influence of the Semantic Structure of Word Problems on Second Graders’ Eye Movements [J]. Journal of Educational Psychology, 1990, 82(2): 359-365.

[5] Low R, Over R. Gender Differences in Solution of Algebraic Word Problems Containing Irrelevant Information [J].Journal of Educational Psychology, 1993, 85(2):331.

[6] Muth K D. Extraneous Information and Extra Steps in Arithmetic Word Problems [J]. Contemporary Educational Psychology, 1992, 17(3): 278-285.

[7] Littlefield J, Riser J J. Finding the Critical Facts: Children’s Visual Scan Patterns when Solving Story Problems that Contain Irrelevant Information [J]. Journal of Educational Psychology, 2005, 97(2): 224-234.

[8] Nicole M McNeil, Bethany Rittle-Johnson, Shanta Hattikudur, et al. Continuity in Representation between Children and Adults: Arithmetic Knowledge Hinders Undergraduates’ Algebraic Problem Solving [J]. Journal of Cognition and Development, 2010, 11 (4):437.

[9] Littlefield J, Riser J J. Semantic Features of Similarity and Children’s Strategies for Identification of Relevant Information in Mathematical Story Problems [J]. Cognition and instruction, 1993, (11): 133-188.

[10] Littlefield J. College Students and Algebra Story Problems: Strategies for Identifying Relevant Information [J]. Reading Psychology, 2006, (2): 6～9.

[11] 岳宝霞，冯虹.眼动分析法在数学应用题解题研究中的应用[J].数学教育学报，2013，22（1）：93-95.

[12] 黄秦安，刘达卓，聂晓颖.论数学欣赏的“含义”“对象”与“功能”——数学教育中的数学欣赏问题[J].数学教育学报，2013，22（1）：8-12.

[13] 徐文彬.试论数学文化视域中的数学学习[J].数学教育学报，2013，22（1）：13-17.

[14] 王名扬，徐沥泉，徐利治.论一种缘自认知心理学及教育学研究的数学认知过程[J].数学教育学报，2013，22（1）：33-36.

[15] 谢圣英，喻平.数学教育中的隐喻研究[J].数学教育学报，2013，22（2）：5-10.

[16] 费祥历，许晓婕.数学文化教育的思考与实践[J].数学教育学报，2012，21（1）：13.

[17] 徐文彬.关于现实社会中儿童学习若干现象的检讨——以“科学数学观”视域下数学学习为案例分析[J].数学教育学报，2012，21（1）：17-20.

[18] 刘振达，王青建，邵茹.从数学史角度研究数学学习动机[J].数学教育学报，2012，21（3）：26-27.

[19] 袁智强.整合技术的学科教学知识研究综述[J].数学教育学报，2012，21（6）：13-18.

[20] 彭瑜，徐速.不同数学学业成就初中生数学焦虑的研究[J].数学教育学报，2012，21（4）：40-43.