三维周期结构弱无条件稳定FDTD算法研究

李洪宇，王发年，刘宗信，2，李林，李军

（1.解放军95972部队甘肃酒泉735018；2.解放军理工大学江苏南京210007）

在电子元器件中，许多结构都具有一维或二维周期性，如光栅、相控天线阵、光电子带隙（PBG）及频率选择表面（FSS）等等。时域有限差分法由于自身的一些优点，如引入周期边界条件（PEC）就可以通过研究一个单元的电磁散射特性来获取整个结构的电磁散射特性，在解决此类问题时具有很大的优势，被广泛用来模拟这些器件的电磁散射特性。但是，传统时域有限差分法受Courant-Friedrich-Lewy（CFL）稳定性条件的限制，在处理一些细小结构如薄层介质、孔、缝等上有局限性。为了消除CFL稳定性条件的限制，人们努力寻找各种无条件稳定算法或弱条件稳定算法。1999年，T.Namiki首先将交变隐式差分方法（Alternating-Direction Implicit Method，ADI）应用到FDTD中，提出了无条件稳定ADIFDTD方法[1]，该算法在分析细微结构电磁问题时，缩短了计算时间，提高了计算效率。由于ADI-FDTD突破了稳定性条件的限制，时间步长可以适当增加，使计算时间大幅减少，因此得到了较为广泛的应用。但是ADI-FDTD法也存在着不足，当时间步长增大时，将会导致较大的数值误差，降低了计算精度。2003年，Binke Huang等人提出了一种弱条件稳定（Weakly Conditionally Stable）的FDTD算法[2]，该算法的的时间步长只由两个方向上的空间步长决定，相对于传统FDTD方法，其稳定性条件减弱，该方法非常适用于在一个方向上具有精细结构的电磁问题的模拟。2007年，Juan Chen等人在双向弱条件稳定FDTD方法的基础上，又提出了一种新的单向弱条件稳定LOD-FDTD方法[3]，该方法的时间步长只由一个方向的空间步长决定，相对于传统FDTD方法其稳定性条件进一步减弱，一经提出，就得到了广泛应用。

当将LOD-FDTD方法用于解决周期结构的电磁散射问题时，跟传统FDTD方法相同，只需在两个方向设置吸收边界，因此UPML要比PML具有优势[4]，因此，本文拟将UPML引入到LOD-FDTD方法中用于解决周期结构的电磁散射问题。

1 算法的差分公式

不失一般性，在电导率为σ，导磁率为σ*的介质中，频域内的Maxwel方程可以写做：

其中：

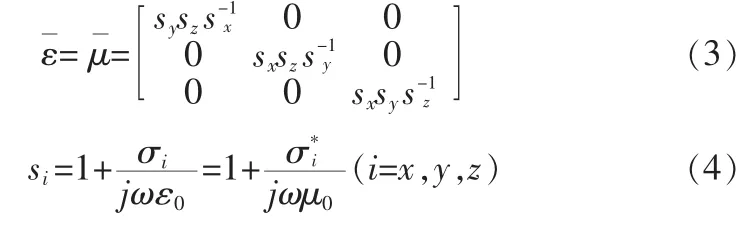
在无损条件下，假设吸收边界设置在z轴方向，即sx=sy=1，这里定义两个辅助变量：

将（5）和（6）式带入（1）和（2）式中，可以得到：

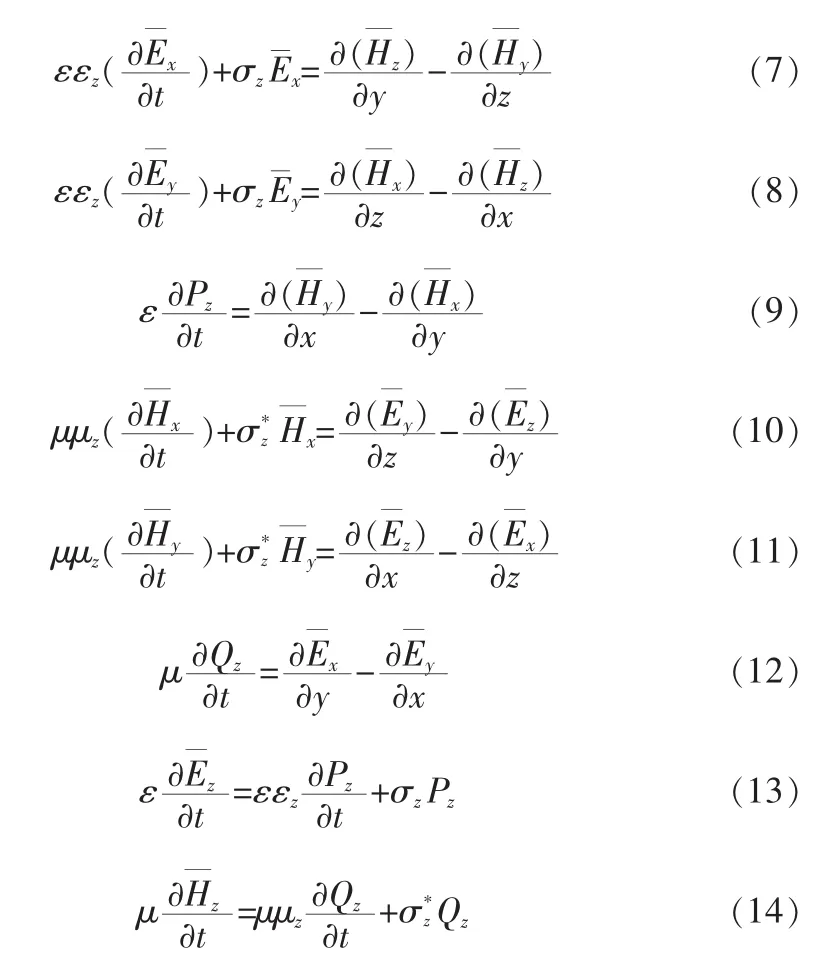
假设窄边沿着x轴方向，应用文献[7]所介绍的弱无条件稳定时域有限差分算法，从方程（7）到（14）可以得到场量Ey、Hz以及辅助变量Qz的下述迭代方程，用同样地方法也可以得到其余场量的相关迭代方程。

显然，（15）式中含有未知场量Hz，对其进行重新排列和替代，可以得到：

场量可以通过求解一特殊的非三角矩阵获得，求得场量后，场量和辅助变量可以通过（16）式和（17）式的直接迭代求得。同理，其余各场量可以按照同样地方法求得。

2 周期结构中的应用

考虑垂直入射波，PBC可以写成下列形式：

其中，Nx1，Nx4代表元胞边界上电场所在的节点位置。将（23）式带入（18）式可以得到：

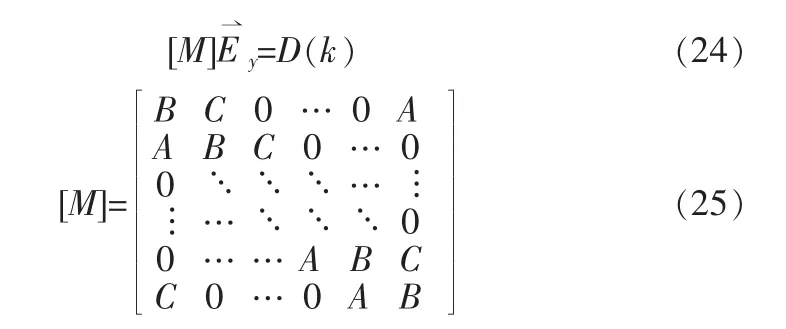
系数矩阵[M]并非三对角矩阵，因此并不能用前向消去和后向迭代法直接求解，应用Sherman Morrison公式，按照文献[6]所介绍的方法可将其化作如下的两个线性方程进行求解：

因此，（24）式的解可以通过下述方程求得：

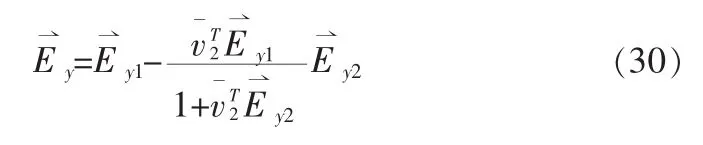
显然，通过观察可以发现（25）式中的矩阵[M]与矩阵[N]相关，矩阵[N]是三对角矩阵，辅助线性方程可以利用文献[8]介绍的前向消去和后向迭代有效解决。

3 数值检验

为了验证所提算法的精度和效率，引入一调制过的高斯脉冲作为入射波，所讨论局域的前端垂直于轴，入射场可写作：

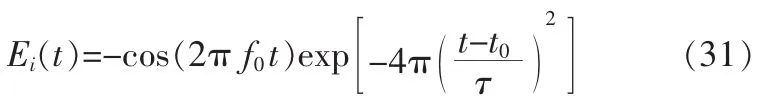
其中：f0=10 GHz，t0=1.125×10-10，τ=1.0×10-10，将它应用于计算周期阵列的反射系数，周期阵列在x方向上带有细缝，如图1所示。参考文献[9]，设置大区域和小区域，称为ΩB和ΩS，大区域计算空间为100×20×318，小区域计算空间为100×20×78，细缝的宽度为0.1 mm，单元尺寸取为Δy=Δz=5Δx=Δ=0.5 mm，计算用16层UPML在方向截断，反射误差表示为：

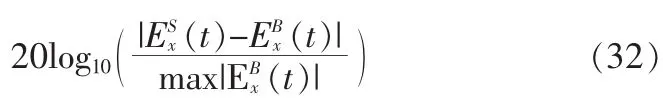
用传统FDTD进行计算时，时间步长必须满足稳定性条件，本文中为用本文所提方法进行计算时，时间步长仅由Δy、Δz决定，为，本文中分别选用Δt=

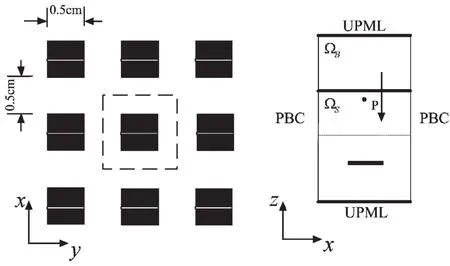
图1 带有细缝的金属薄片周期阵列Fig.1 Periodic array of metallic patches with thin slots

为了便于比较，图2给出了用本文所提方法将UPML层设置为4层、16层以及用传统的FDTD方法将UPML设置为16层时的数值反射误差。当用16层UPML在方向截断时，本文所提方法与传统FDTD算法的数值反射误差相差很小，即使用本文所提方法，设置4层UPML用于截断计算局域时，反射误差也在-50 dB以下。

图3为使用不同的时间步长计算时的周期结构的反射系数随频率的变化关系，从图中可以看出，既是时间步长选为时，本文所提方法的计算结果也与传统FDTD方法的计算结果保持高度一致。但其计算效率却比传统FDTD算法的计算效率高出好多，使用本文所提方法仅需要169.2 s，而传统FDTD算法却要耗时385.9 s。

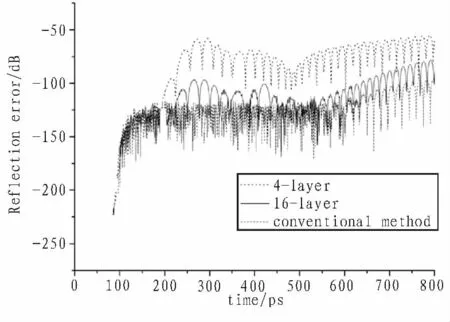
图2 本文所提方法的反射误差与传统FDTD方法反射误差的比较Fig.2 Comparison of the reflection error of conventional method and proposed method

图3 本文所提方法取不同时间步长的反射系数与传统TDTD（Δt=Δ/6c）反射系数的比较Fig.3 Comparison of reflection coefficient for conventional method（Δt=Δ/6c）and proposed method

4 结论

本文中，将UPML应用于LOD-FDTD算法中用于解决周期结构的电磁散射问题，从数值计算结果中可以得出，用本文所提的方法，当沿轴方向设置16层UPML层时，可将反射误差降到-100 dB以下，即使设置4层UPML，反射误差也在-50 dB以下。因此，本文所提方法在解决周期结构电磁散射具有一定的优势。

[1] T.Namiki.A new FDTD algorithm based on alternatingdirection implicit method[J].IEEE Trans.Microwave Theory Tech.，1999，47（10）：2003-2007.

[2] Binke Huang，Gang Wang，Yansheng Jiang.A Hybrid implicit-explicit FDTD scheme with weakly conditional stability[J].Microwave and Optical Tech.Lett.，2003，39（2）:97-101.

[3] Chen J，Wang J.3-D FDTD method with weakly conditional stability[J].Electronics Letters，2007，43（1）：2-3.

[4] Berenger J P.A perfectly matched layer for the absorption of electromagnetic waves[J].J.Comput.Phys.，1994（114）：185-200.

[5]Taflove A，Hagness S C.Computational Electrodynamics:The Finite-Difference Time-Domain Method[M].second edition，Boston，MA:Artech House，2000.

[6] Thomas J W.Numerical Partial Differential Equations:Finite Difference Methods[M].Berlin，Germany:Springer Verlag，1995.

[7] Huang B K，Wang G，Jiang Y S，et al.A hybrid implicit explicit FDTD scheme with weakly conditional stability[J].Microw.Opt.Tech.Lett.，2003（39）：97-101.

[8] Zhao A P.Two special notes on the implementation of the unconditionally stable ADI FDTD method[J].Microw.Opt.Technol Lett，2002，33（4）：273-277.

[9] Thomas G M，Jeffrey G B，Taflove A，et al.Theory and application of radiation boundary operators[J].IEEE Trans.Antennas Propagat.，1988，36（12）:1797-1812.