一种陀螺摆式球形驱动机构动力学模型分析
2013-03-27张湖川王雅君朱亚蓉
刘 忠,张湖川,武 颖,2,王雅君,朱亚蓉,刘 焱
(1.首都航天机械公司,北京 100076;2.太原理工大学机械工程学院,山西 太原 030024)
0 引 言
如图1所示的球形驱动装置由转动轴相互正交的两个万向节和一个连杆-转子机构组成。与球体内部相固连的万向节称为外环,只能绕固连轴转动;另一个万向节固连在外环上,因此,称之为内环,可以绕内环固连轴转动。内环和外环的转动轴相互垂直。无质连杆固连在平面内,与内环的转动轴相垂直。均质对称的转子偏离球心而固连在连杆上。在外环和内环的转动轴上分别施加转动力矩,转子在内环和外环的作用下,在半径为l的球面上运动(球面的球心与球体的球心重合),改变了整个系统的质心位置,即势力场的分布,球体则在驱动装置的反作用下滚动。当外环的转动轴平行于水平面时,驱动装置的构型类似一个陀螺摆装置,因此称图1所示机构为陀螺摆式球形驱动机构。陀螺摆式球形机构在球形机器人的设计中得到了广泛的应用。本文利用拉格朗日法建立了系统的动力学模型,并计算其平衡点。
1 动力学建模
设如图1所示,陀螺摆式球形机器人的球心速度为u,与正北方向成α角,旋进角速度为α̇。为了推导在加速度u̇的作用下,驱动装置的运动微分方程,建立如图2所示的坐标系:球体的基础坐标系为∑sphere{X,Y,Z}(即为惯性坐标系的平移坐标系),外环的坐标系为 ∑outer gimbal{ξ′,η′,ζ′},内环的坐标系 为 ∑inner gimbal{ξ,η,ζ} 以 及 转 子 的 坐 标 系 为∑rotor{x,y,z},而且,所有的坐标原点均位于点O处,轴ξ与轴ξ′重合同向,轴η′与轴Z重合反向,轴ζ与轴z重合同向。这样,外环可以绕坐标系∑sphere的Z轴自由转动,转角记为 ;内环可以绕坐标系 ∑outer gimbal的轴ξ自由转动,转角记为θ,轴ξ始终位于XY平面内;转子的对称轴z垂直于轴ξ,可以绕坐标系∑inner gimbal的轴ζ(轴z)自由转动,转角记为ψ。

图1 陀螺摆式球形驱动机构示意图

图2 陀螺摆式球形驱动机构坐标系
在球体的基础坐标系内,转子的姿态可以由3个欧拉角ϕ,θ和ψ确定。如果忽略外环和内环的转动惯量,那么转子的运动方程可以表示为[1]:

其中,T为驱动机构的动能,列向量矩阵{ }N0的分量分别为输入力矩在转动轴ξ,η和ζ上的投影。列矩阵{ }
∂T/∂Ω 的 分 量 分 别 为 ∂T/∂Ωξ、∂T/∂Ωη和∂T/∂Ωζ,其中 Ωξ,Ωη和 Ωζ分别转子的角速度在转动轴ξ,η和ζ上的投影。列矩阵{ }∂T/∂υ的分量分别为 ∂T/∂υξ,∂T/∂υη和 ∂T/∂υζ,其中 υξ,υη和 υζ分别转子的速度分量。
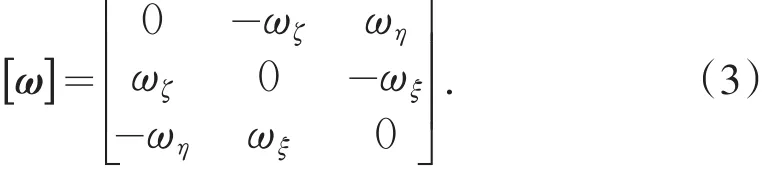
距阵式(3)为一斜对称矩阵,其中ωξ,ωη和ωζ分别为内环的角速度在转动轴ξ,η和ζ上的投影。设基础坐标系在惯性坐标系上的角速度投影分别为ωX=0,ωY=α̇和ωZ=0,且外环对于球体的转动角速度为ϕ̇。那么,外环的角速度在转动轴ξ′,η′和ζ′上的投影分别为:

内环对于外环的转动角速度为θ̇,那么,内环的角速度在转动轴ξ,η和ζ上的投影分别为:

转子绕对称轴z的转动角速度为ψ̇=0,那么,转子的角速度在转动轴ξ、η和ζ上的投影分别为:

设点O的速度(球体的速度)为:

若设v为转子质心的速度,列向量{r}为转子质心C到点O的矢径,即{r}=[0 0 -l]T,其中l为转子质心到点O的长度。那么u和v之间的联系可以表示为矩阵形式:

其中,[ω ]如式(3)所示,则有:

设转子的质量为m,对于惯性主轴ξ,η和ζ的转动惯量分别为A,A和C,并且忽略外环和内环的转动惯量,可以得到转子的动能T为[2]:

将上式代入式(1),得到力平衡方程:
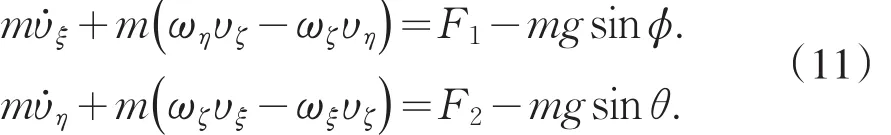
其中,F1和F2分别为球体对转子的反作用力在转动轴ξ和η上的投影。将式(10)代入式(2)得到力矩平衡方程:

将式(11)代入式(12)得到关于转子的动量方程为
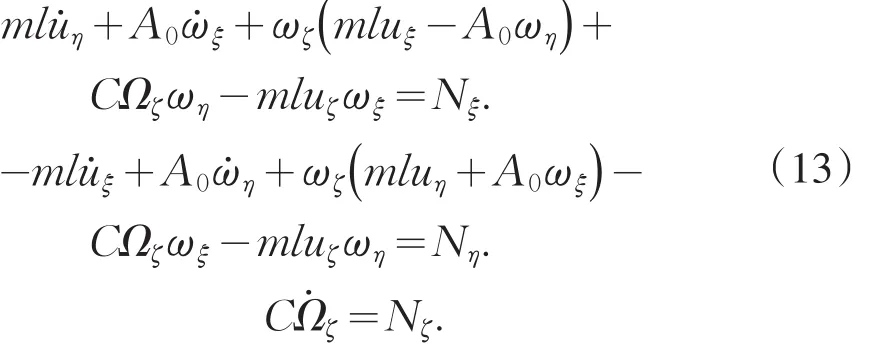
式中:A0=A+ml2,Nξ=-mgl sinθNη=-mgl sinϕ.
2 平衡点计算
对于欠驱动陀螺摆球形机器人有Nζ=0,且转子关于转动轴z对称,那么,由式(13)中的第3式得:

对于小量ϕ和θ有:

因此,忽略高阶项,式(13)中的第1式和第2式可以分别简化为:
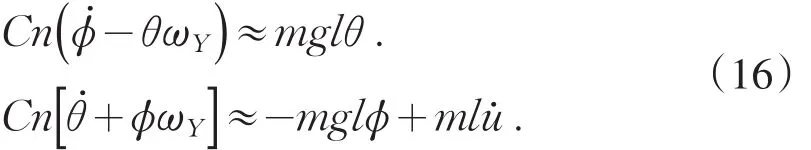
如果设:

那么式(17)可以简化为:

由方程组(18)可得:

当u̇不变,即球体稳定运行时,微分方程(19)的解为:

将式(20)代入方程组(18)的第2式,并忽略高阶项,可以得到关于θ̇的微分方程的解为:
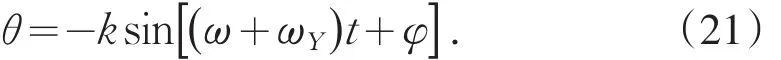
由微分方程组(18)解的形式可以看出转子的对称轴z(轴ζ)在平衡位置是自由振动的,平衡位置为:

3 结 论
建立了一种球形驱动装置的动力学模型,并推倒其平衡点。该球形驱动装置由转动轴相互正交的两个万向节和一个连杆-转子机构组成,通常被称为陀螺摆式球形驱动机构。陀螺摆式球形机构在球形机器人的设计中得到了广泛的应用。
[1] 孙汉旭,王亮清,贾庆轩,等.BYQ-3球形机器人的动力学模型[J].机械工程学报,2009,45(10):8-14.
[2] ZHAN Qiang,JIA Chuan,MA Xiaohui.Mechanism design and motion analysis of a spherical mobile robot[J].Chinese Journal of Mechanical Engineering,2005,18(4):542-545.
