带p－Laplacian算子四阶四点边值问题的迭代解

2013-03-27茹凯韦煜明倪黎

河池学院学报 2013年2期

茹凯，韦煜明，倪黎

(广西师范大学数学科学学院，广西桂林 541004)

0 引言

高阶微分方程边值问题在物理、化学和生物等领域中有着极为丰富的源泉，研究它的解的存在性具有重要的理论意义和实践意义。近年来，高阶微分方程特别是四阶微分方程的边值问题受到了许多学者的关注，取得了一些成果。文献［1］考虑具有p－Laplacian算子的四阶四点边值问题的迭代解，文献［2］利用Avery－Henderson不动点定理研究具有p－Laplace算子的四阶三点边值问题，给出了存在至少两个正解的充分条件。文献［3］考虑下列具有p－Laplace算子的四阶三点边值问题

文献［4］利用上下解方法研究了下列四阶四点边值问题

受上述文献启发，本文讨论了不同于上述方程的一类具有p－Laplace算子的四阶四点边值问题

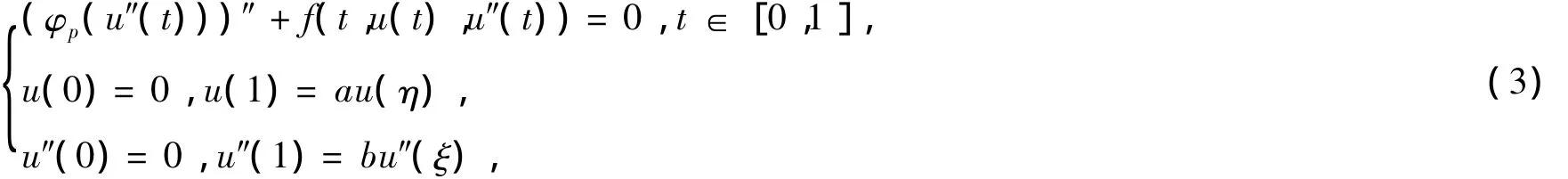
1 预备知识

定义1:设α，β∈W分别称为边值问题(3)的下解和上解，若

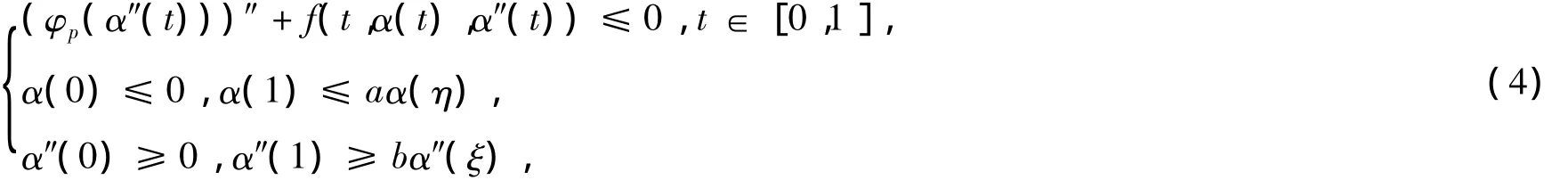
引理1［4］:若 a(t)∈ C［0，1］，0 ≤ aη ＜ 1，则下列二阶三点边值问题

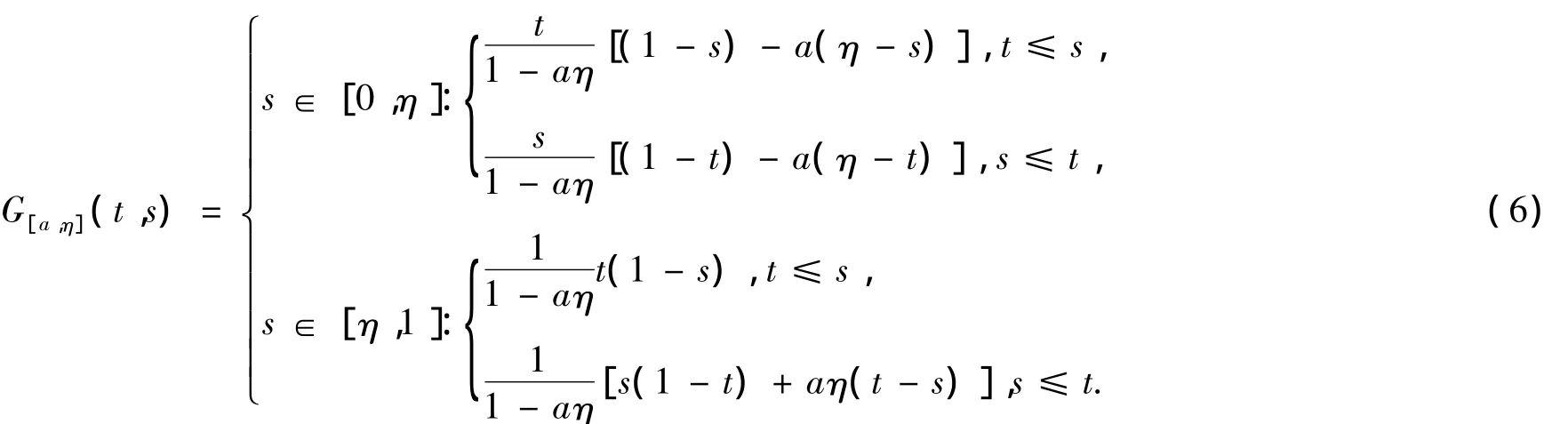
引理2［4］:若 a(t)∈ C［0，1］，0 ≤ bξ＜ 1，则下列二阶三点边值问题

引理3:设a，b，ξ，η 是非负常数，且0 ＜ ξ，η ＜ 1，0 ＜ a，b ＜ 1，1－bξ＞ 0，如果x(t)∈W满足

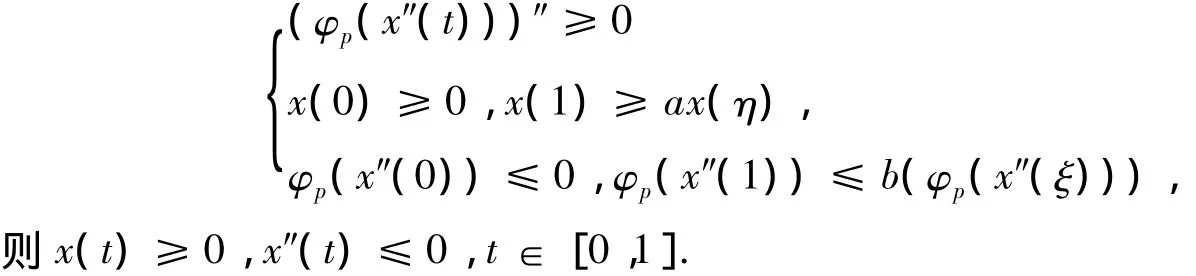
证明:设 w(t)= φp(x″(t))，则

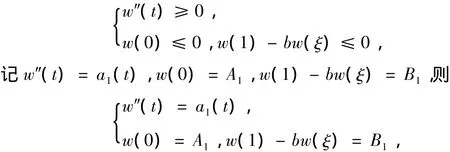
w(t)可表示为

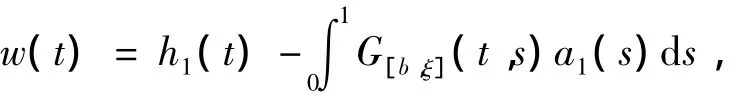
z(t)可表示为

引理3证毕。

定理1［7］:设D是半序Banach空间X的子集，F∶D→X是单增的，如果存在x0，y0∈D使得x0≤y0，＜x0，y0＞⊂D，并且x0，y0分别是方程x－F(x)=0的下解和上解，则当下面的条件之一成立时，方程x－F(x)=0在序区间＜x0，y0＞上有极小解x*和极大解y*，使得x*≤y*.

(1)K正规且F紧连续;

(2)K正则且F连续;

(3)X自反，K正规且F连续或者弱连续。

条件(H):

1)ξ，η，a，b，p 是非负常数，且 0 ＜ ξ，η ＜ 1，0 ＜ a，b ＜ 1，p ＞ 1;

2)边值问题(1)存在上下解 β(t)和 α(t)，满足 α(t)≤ β(t)，α″(t)≥ β″(t)，t∈［0，1］;

3)对 α(t)≤ x1≤ x2≤ β(t)，β″(t)≤ y≤ α″(t)，t∈［0，1］，有 f(t，x1，y)≤ f(t，x2，y);

4)对 β″(t)≤ y1≤ y2≤ α″(t)，α(t)≤ x≤ β(t)，t∈［0，1］，有 f(t，x，y1)≥ f(t，x，y2).

2 主要结果

定义算子T:Ω → C2［0，1］，其中 G［a，η］，G［b，ξ］分别由(6)式和(7)式给定。易证 T 是全连续算子。记α0(t)= α(t)，β0(t)= β(t)，由αn(t)= (Tαn－1)(t)，βn(t)= (Tβn－1)(t)定义序列{αn}和{βn}.

定理2:若条件(H)成立，则由(8)式定义的序列{αn}和{βn}均收敛于(3)的解。

对有α(t)≤x(t)≤β(t)，β″(t)≤x″(t)≤α″(t)，且|x'(t)|≤N.令ω(t)=(Tx)(t)，由T 的定义知，ω，φp(ω″)∈ C2［0，1］. 另一方面，由下解 α(t)的定义及条件(H)，得

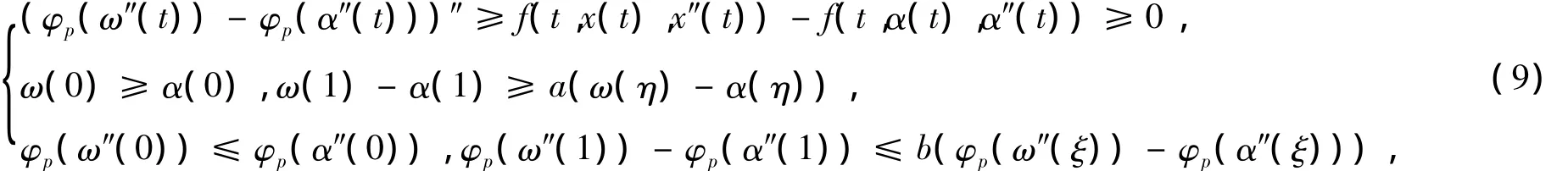
令 y= φp(ω″(t))－ φp(α″(t))，则 y在［0，1］上二次可微，且 y″≥0，y(0)≤0，y(1)≤ by(ξ). 因此，由引理3，我们有 y(t)≤0，对 t∈［0，1］. 即 φp(ω″(t))≤ φp(α″(t))，对t∈［0，1］. 又由于 φp为单调增函数，故 ω″(t)≤α″(t)，对t∈［0，1］.即(ω(t)－ α(t))″≤0，对t∈［0，1］.综合引理3及(9)式，有ω(t)≥α(t)，对 t∈［0，1］.利用类似的方法，可以证明ω(t)≤β(t)，ω″(t)≥β″(t)，对t∈［0，1］.于是α(t)≤ω(t)≤β(t)，β″(t)≤ ω″(t)≤ α″(t)，t∈［0，1］. 显然 ω″(t)≤ max(‖α″‖0，‖β″‖0)，且存在 t0∈［0，1］使