基于属性选择法的朴素贝叶斯分类器性能改进❋

焦 鹏，王新政谢鹏远

（1.海军航空工程学院，山东烟台264001；2.解放军91055部队，浙江台州318050）

基于属性选择法的朴素贝叶斯分类器性能改进❋

焦 鹏1，❋❋，王新政1，谢鹏远2

（1.海军航空工程学院，山东烟台264001；2.解放军91055部队，浙江台州318050）

为提高朴素贝叶斯（Naive Bayesian）分类器的分类准确率，对朴素贝叶斯属性选择算法及假设属性概率值先验分布中的参数设置问题进行分析，提出将属性先验分布的参数设置加入到属性选择的过程中，并研究当先验分布服从Dirichlet分布及广义Dirichlet分布情况下的具体调整步骤。以UCI数据库为例进行仿真实验，结果表明当先验分布服从广义Dirichlet分布时，该方法可提高分类的准确率，如Parkinsons数据集，效率可提升13.32％。

朴素贝叶斯分类器；先验分布；属性选择法；广义Dirichlet分布

1 引 言

在数据挖掘领域，朴素贝叶斯分类器（Naive Bayesian Classifier，NBC）由于运算速度快、分类准确率较高，得到了广泛的应用。NBC假设一个属性值对给定类的影响独立于其他属性值，这样的假设有助于提高运算效率，然而现实中往往不能满足。研究者提出各种方法对NBC的分类性能进行改进，如树增强朴素贝叶斯（Tree Augmented Naive Bayes，

TAN）［1］、惰性贝叶斯规则（Lazy Bayesian Rules）［2］、特征加权（Weighted Naive Bayes，WNB）［3］等方法。这些方法与NBC相比通常具有较好的分类精度，在一定程度上改进了NBC的性能。研究显示，当数据样本属性之间相关程度很高时会降低分类准确率，因此希望NBC使用的属性集合尽可能地服从条件独立，即需要一个属性选择机制［4］。在众多的属性选择方法中，朴素贝叶斯属性选择算法（Selective Naive Bayesian Algorithm，SNB）能有效剔除多余或影响分类结果的属性，因此常被用于NBC中［5］。另外，为了改善NBC的分类效果，通常假设属性的可能值服从某种先验分布，一般是Dirichlet分布或广义Dirichlet分布。针对先验分布的参数设置已有很多学者提出各种设定方法［1］。在以往的研究中，属性选择结束后一般会直接进行分类而不考虑先验分布。本文将各属性先验分布的参数调整加入到属性选择的过程中使之成为一个整体，即首先运用SNB算法对样本数据集合进行属性选择，再根据其得出的属性选择顺序对选出的属性群进行参数的个别调整。通过对UCI数据库中的10个样本数据集合进行分析，仿真实验结果表明与以往的方法相比，本文提出的方法可提高分类准确性。

2 基础理论分析

2.1 朴素贝叶斯分类器

NBC利用贝叶斯准则（Bayesian Decision Rule）以及属性间条件独立假设作为分类的依据［6］。根据贝叶斯定理，假设有n个属性X1，X2，…，Xn，其中一笔数据x＝（x1，x2，…，xn）属于第j个类别值的概率为Cj：

其中，p（Cj｜x）表示在给定某项样本数据下分类到类别值Cj的概率，称为后验概率（Posterior Probability）；p（x）表示数据x出现的概率。比较不同类别值的后验概率时，式（1）可以简化为

根据NBC的属性条件独立假设，将式（2）展开：

因此，若某一类别值Cj的后验概率最大，NBC可预测该笔数据x的类别值为Cj。

2.2 朴素贝叶斯属性选择算法

文献［7］将属性选择法分成Filter和Wrapper两种。Filter方法根据统计测度分析属性之间的关系选择属性，不考虑选择的属性是否影响特定分类器的表现。而Wrapper方法在选择过程中使用分类器的表现评估属性的重要性。由于Wrapper方法考虑分类器的表现来筛选属性，对未知的数据有较好的分类准确率，而Filter方法不需要反复地求得分类结果，因此执行速度较快。

SNB算法是由文献［5］提出，属于Wrapper方法，其运行流程如图1所示。初始阶段设定S为空集合，从样本数据中选取一个属性到朴素贝叶斯分类器中做分类并计算分类准确率。重复这个过程直到样本数据中所有属性各自对应的分类准确率都已知，选择使分类准确率最高的属性Xi加入S中，此时Xi就是NBC选择的第一个属性。从样本数据中计算未被选择的属性配合Xi得到的分类准确率，选出与之配合能使分类准确率最高的属性Xj，Xj即为第二个选择的属性，重复以上步骤直到分类准确率不再提升。SNB算法的特点是采用前向搜索属性的方法，即初始的属性集合不包含任何属性，一次选择一个属性直到分类准确率不再提升为止。经过实验发现，SNB算法使用较少的属性但分类准确率较高，说明该分类方法有过滤冗余属性的功能。

图1 SNB算法流程图

3 先验分布的参数设定

3.1 先验分布的参数设定

使用NBC进行分类时使用数据样本集合中的所有属性，并通过调整先验分布中的参数来提高分类准确率。而SNB算法则是通过选择对分类准确率真正有帮助的属性供NBC使用。由于筛选的过程耗费时间，因此先验分布的参数常使用Laplace Estimator用以满足无信息性，使得属性可能值的出现概率期望值相同。

文献［8］在实验研究中针对Dirichlet部分依序测试αi，发现αi＝60后分类准确率与αi成反比。因此对每个属性做参数设定时，将参数αi的范围设定为［1，60］，并取其中的整数。除了限定范围外，调整参数时需满足无信息性的限制，即在此条件下评估各事件的发生概率，都应给定相同的估计值且总和为1。此时各个变量对应的期望值应相同，但是不同的先验分布推导出的期望值公式不同，参数的限制也有所差异。对Dirichlet分布而言，推导出的结果为各参数需设定相同的值（α1＝α2，…，＝αk＋1），以此限制在［1，60］作调整满足无信息性。广义Dirichlet分布在无信息性的限制满足所有参数必须满足式（4）：

由此可知，只要αi已知，便可通过式（4）求得βi的值，因此无论是Dirichlet分布还是广义Dirichlet分布都只需调整参数αi。对于整个样本数据的所有属性做参数设定时，先选择的属性对接下来其他属性的最优参数设定有很大的影响。因此首先判断各属性对分类的重要性，重要性最高的属性优先调整参数和决定先验分布。而SNB算法在挑选属性的过程可看作属性重要性的排序过程，根据SNB算法选择的顺序作为属性参数调整的顺序。

3.2 Dirichlet分布

定义1：随机向量θ＝（θ1，θ2，…，θk）满足θ1＋θ2＋…＋θk≤1且θj＞0（j＝1，2，…，k），如果其概率密度函数为

其中，αj＞0（j＝1，2，…，k＋1）且α＝α1＋α2＋…＋αk＋1，则随机向量θ服从k维Dirichlet分布，记作θ～DK（α1，α2，…，αK；αK＋1）。

假设数据样本中某个属性有k＋1个可能值，令随机向量θ＝（θ1，θ2，…，θk）为该属性前k个可能值对应的出现概率，且θ～DK（α1，α2，…，αK；αK＋1）。令随机向量y＝（y1，y2，…，yk＋1）代表此属性k＋1个可能值分别的发生次数，yj表示此属性第j个可能值出现的次数，如果yθ服从多项分配，根据Dirichlet分布的共轭性质可推得后验概率分布y～DK（α′1，α′2，…，α′K；α′K＋1），其中α′j＝αj＋yj，j＝1，2，…，k＋1表示根据收集样本数据推导出属性可能值的出现概率同样服从Dirichlet分布，不过参数值有所改变。如果θm为θ的一个变量，则θm在给定y的条件下，期望值为

其中y＝y1＋y2＋…＋yk＋1。与NBC使用后验概率进行分类相比，此处将后验分布的期望值作为后验概率进行计算。当一项新的样本数据出现时，就可利用式（6）计算在给定类别下属性的某个可能值发生的概率E（θm｜y），再利用式（3）找出使后验概率最大的类别值，作为此项样本数据的预估类别值。

调整步骤如下：

（1）将所有属性的参数值设定为Laplace Estimator，利用SNB算法选择一组属性，假设共选择m个属性；

（2）针对选择属性中的第一个属性参数，计算α1＝α2，…，＝αk在［1，60］之间各整数的分类准确率，选择使分类准确率最高的参数值为，表示第一个属性的最优参数值；

（3）设定第一个属性的α1＝α2，…，＝αk＋1＝，再针对第二个选择的属性参数计算在［1，60］之间整数的分类准确率，选择使分类准确率最高的参数值设定为，使用同样的方法找出。

3.3 广义Dirichlet分布

定义2：随机向量θ＝（θ1，θ2，…，θk）满足θ1＋θ2＋…＋θk≤1且θj＞0（j＝1，2，…，k），如果其概率密度函数为

其中，参数αj，βj，λj满足αj＞0（j＝1，2，…，k），βj＞0（j＝1，2，…，k），λk＝βk－1及λj＝βj－αj＋1－βj＋1（j＝1，2，…，k－1），则随机变量θ服从k维广义Dirichlet分布。记作θ～GDK（α1，α2，…，αK；β1，β2，…，βK）。

与Dirichlet分布在朴素贝叶斯分类器的作用一样，当假设样本数据中某属性服从广义Dirichlet分布，如果该属性有k＋1个可能值，令随机向量θ＝（θ1，θ2，…，θk）为该属性前k个可能值的概率，且θ～GDK（α1，α2，…，αK；β1，β2，…，βK）。令随机向量y＝（y1，y2，…，yk＋1）表示该属性的k＋1个可能值分别发生的次数，yj表示此属性第j个可能值出现的次数。如果y｜θ服从多项分配，由于广义Dirichlet分布也具有共轭性质，可知后验概率分布

θ｜y～GDK（α′1，α′2，…，α′K；β′1，β′2，…，β′K）。如果θm是θ的一个变量，则θm在给定y的条件下，期望值为

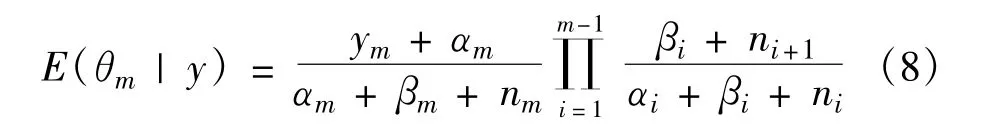
其中，j＝1，2，…，k，m＝1，2，…，k。

由式（8）和式（9）可知，在给定类别值下，除了估计某属性的最后一个可能值的发生概率使用式（9）之外，估算其他可能值的发生概率都可采用式（8）计算。最后再利用式（3）找出具有最大后验概率的类别值，作为此项样本数据的预估类别值。

调整步骤如下：

（1）将所有属性的参数值设定为Laplace Estimator后由SNB算法挑选出m个属性；

（2）针对第一个属性的首个参数α1计算在［1，60］之间整数的分类准确率，挑选使分类准确率最高的参数值为，表示第一个属性的最优参数值；

（3）假设α1＝，针对α2计算在［1，60］之间整数的分类准确率，选择使分类准确率最高的参数值设定为，用同样的方法找出，并通过式（4）计算相应的βi；

（4）针对SNB挑选的第二个属性，以步骤1～2的方式调整其参数，并采用相同的方式找出第3～m个属性的最优参数值。

4 实验验证

4.1 模式评估

［9］，整理得出以下两个指标。

（1）分类准确率：采用K-fold交互认证，将样本数据中的数据分成K个集合，一个集合称为一个fold。当其中一个fold作为测试的集合时，其他K-1个fold结合成一个训练数据，之后重复进行K次，直到K个fold都作为测试的集合，最后取K次分类准确率的平均值作为指标。

（2）属性个数：比较选择的属性和通过属性选择法减少的属性个数，如果只需少量属性即可获得良好的分类准确率，表示该属性选择法确实能有效地过滤冗余属性。

4.2 实例验证

本节针对UCI［10］上的10个样本数据集合进行计算并评估其性能。

表1为样本数据集合的相关属性。将K-fold交互式认证法的K值设定为5，使得样本数据集合最小的tae集合在每个fold平均有30项，因此不会因为测试项数量过小导致结果无统计意义。另外，如果样本数据集合中某些属性出现遗漏值则忽略，只使用其他没有遗漏值的属性作运算。由于NBC无法直接使用连续型属性，应将数据离散化。在离散化的方法中，ten-bin是将连续型属性分成10个等区间，并按照属性值大小放入这10个区间，即变成有10个可能值的离散属性。本文选用的资料文件包含连续属性和离散属性，样本数量从151～8 124不等，目的就是研究本文提出的方法在各种情况下的分类准确率，得出较为客观的结论。

表1 实验样本数据属性及属性选择结果Table 1 List of sample attributes and selected results

4.3 测试结果及分析

表2列出各模式下选择的属性群及个数，其中NBC表示朴素贝叶斯分类器使用的属性个数，即所有属性个数，SNB表示本文方法使用的属性个数。

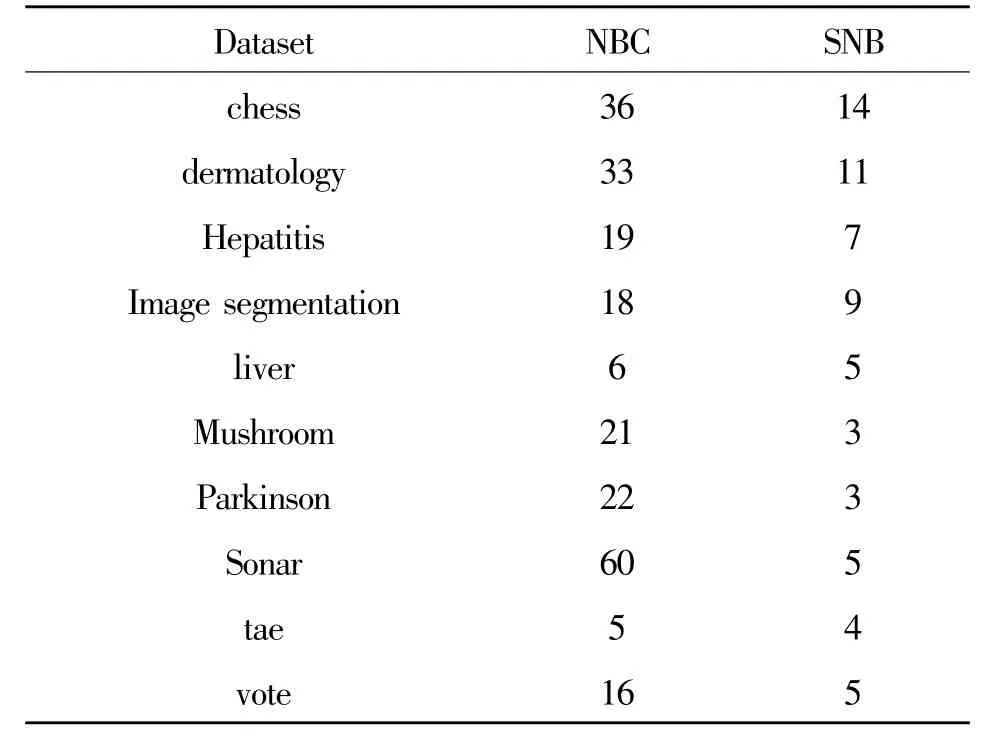
表2 属性选择结果Table 2 List of attribute selection results

表3为所有样本数据集合在各模式下的分类准确率，其中的粗体数值表示各样本数据集合最高的分类准确率。NBC表示朴素贝叶斯分类器，使用Laplace Estimator。SNB表示使用SNB选出的属性做预测的分类准确率，使用Laplace Estimator。MD表示先验分布为Dirichlet分布，调整出最优参数的分类准确率。MG表示先验分布为广义Dirichlet分布，调整最优参数的分类准确率。分类效果如图2所示。

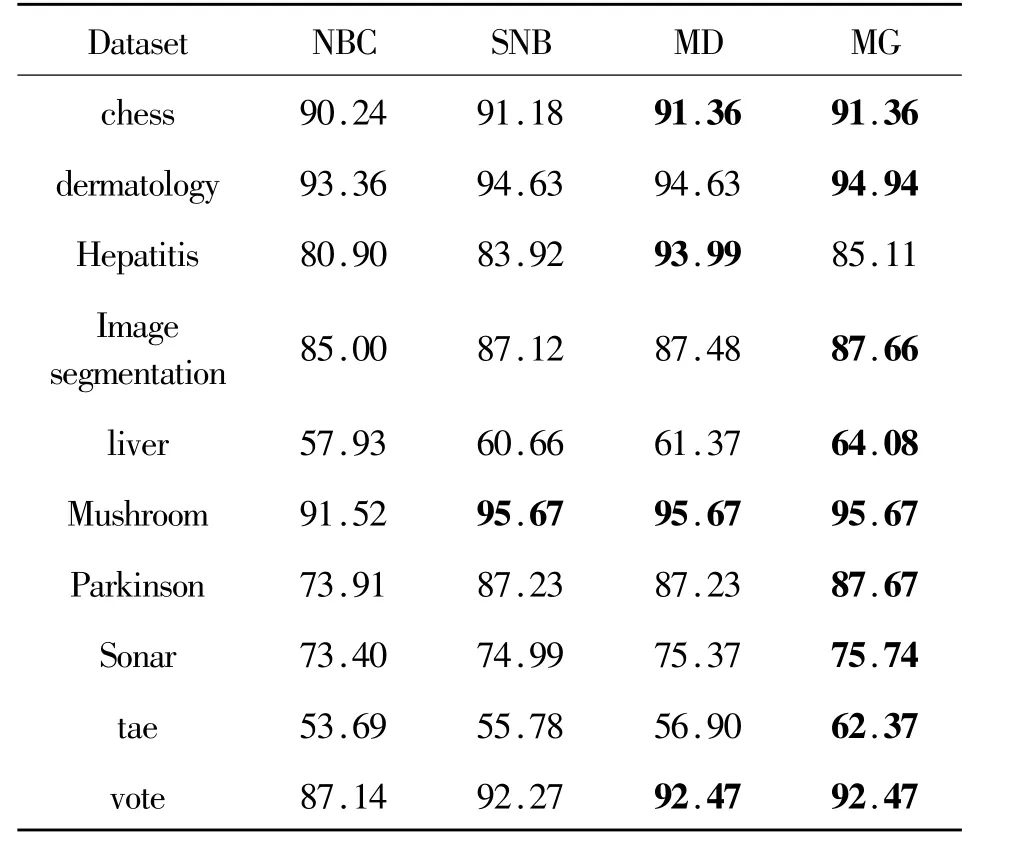
表3 分类准确率汇总表Table 3 List of classification accuracy

图2 分类结果对比图

分析以上结果可知，在各个样本数据集合中，SNB的准确率要优于NBC。例如Parkinsons数据集，NBC使用22个属性的分类准确率为73.91％，而SNB筛选出3个属性的准确率为87.23％，效率提升13.32％。这说明在实际样本数据集合中并非每个属性都具有分类价值，属性间也不完全服从条件独立的假设，以上两点都会影响NBC的分类准确率。

SNB算法筛选出的属性数量与原始属性数量无关，这说明分类准确率不再提升时SNB算法即终止，因此选择的属性数量只与各阶段已选入的属性群计算的分类准确率有关，与原始属性无关。

当先验分布服从广义Dirichlet分布时，准确率在多数样本数据集合中最高。一般而言，广义Dirichlet分布比Dirichlet分布更能提升NBC的准确率，但受样本数据集合内噪声的影响，有可能使得服从Dirichlet分布时准确率更高。本文研究的属性集合经过SNB算法选择，可基本滤除干扰属性的影响，在这样的属性集合下可使广义Dirichlet充分发挥其效用。

5 小结

本文运用SNB算法对样本数据集合进行属性选择，在属性选择的过程中针对已选出的属性，分析各个属性的特点加入最适合该属性的先验分布后再做选择，并根据选择过程中的分类准确率调整先验分布的参数，最终产生的一组具有适合先验分布的属性集合以提高分类准确率。仿真实验结果表明该方法可在保证分类效率的前提下提高分类准确率。在分析SNB算法的分类结果时，发现准确率不再上升即停止选择的准则过于严格，即使目前的准确率下降，继续选择若干个属性后仍有可能进一步提高分类准确率。在下一步研究中考虑设置一个缓冲区间，当准确率下降在某个范围内时仍可以进行选择。这样可避免由于选择属性过少对分类准确率的影响，使得分类效果得到进一步的改善。

参考文献：

［1］Friedman N，Geiger D，GoldszmidtM.Bayesian network classifiiers［J］.Machine Learning，1997，29（2/3）：131－163.

［2］Zheng Zijian，Webb G I，Ting Kaiming.Bayesina rules：A lazy semi－semi－Naïve Baesian learning technique competitive to boosting decision trees［C］//Proceeding of the 16th International Conference on Machine Learning.Bled，USA：IEEE，1999：493－502.

［3］Webb G I，JPazzaniM J.Adjusted probability naïve Bayesian induction［C］//Proceeding of the 11th Australian jiont Conference on Artificial Intelligence.Adelaide，Australia：IEEE，1998：285－295.

［4］Ioan Pop.An approach of the naive Bayesian classifier for the document classification［J］.General Mathematics，2006，14（4）：135－138.

［5］Langley P，Sage S，Induction of selective bayesian classifiers［C］//Proceedings of UAI-94 10th International Conference on Uncertainty in Artificial Intelligence.Seattle，WA：IEEE，1994：399－406.

［6］John G H，Kohavi R，Pfleger K.Irrelevant features and the subset selection problem［C］//Proceedings of the 11th International Conference on Machine Learning.New Brunswick，NJ：IEEE，1994：121－129.

［7］Kim Chanju，Hwang Kyu-Baek.Naive Bayes classifier learningwith feature selection for spam detection in social bookmarking［C］//Proceeding of Europe Conference on Machine Learning and Principles and Practice of Knowledge Discovery in Databases.Antwerp，Belgium：IEEE，2008：184－198.

［8］余芳，姜云飞.一种基于朴素贝叶斯分类的特征选择方法［J］.中山大学学报（自然科学版），2004，43（5）：118－120.YU Fang，JIANG Yun-fei.Selection method based on the characteristics of the naive Bayesian classifier［J］.Zhongshan University University（Natural Science Edition），2004，43（5）：118－120.（in Chinese）

［9］秦锋，任诗流，程泽凯，等.基于属性加权的朴素贝叶斯分类算法［J］.计算机工程与应用，2008，44（6）：107－109.QIN Feng，RENShi-liu，CHENGZe-kai，etal.Naive Bayes classification algorithm based on attribute weighting［J］.Computer Engineering and Applications，2008，44（6）：107－109.（in Chinese）

［10］Frank A，Asuncion A.UCIMachine Learning Repository［EB/OL］.（2010）［2012－07－15］.http：//archive.ics.uci.edu/ml.

焦鹏（1980—），男，陕西西安人，2009年获硕士学位，现为博士研究生，主要从事智能信息处理、复杂设备故障预测及诊断研究；

JIAO Peng was born in Xi′an，Shaanxi Province，in 1980.He received the M.S.degree in 2009.He is currently working toward the Ph.D.degree.His research concerns intelligent information processing and prognosticsand diagnosisof complex equipment.

Email：Jiaopeng－NEAU＠hotmail.com

王新政（1949—），男，陕西汉中人，海军航空工程学院教授、博士生导师，主要从事信息对抗技术、智能设备检测研究；

WANG Xin-zheng was born in Hanzhong，Shaanxi Province，in 1949.He isnow a professor and also the Ph.D.supervisor.His research concerns information warfare and intelligent test technology.

谢鹏远（1980—），男，陕西安康人，2009年获硕士学位，现为工程师，主要研究方向为智能信息处理及电子对抗。

XIE Peng-yuan was born in Ankang，Shaanxi Province，in 1980.He received the M.S.degree in 2009.He is now an engineer.His research interests include intelligent information processing and electronic countermeasures.

Performance Improvement of Naive Bayesian Classifier Based on Feature Selection

JIAO Peng1，WANG Xin-zheng1，XIE Peng-yuan2
（1.Naval Aeronautical Engineering University，Yantai264001，China；2.Uint91055 of PLA，Taizhou 318050，China）

In order to improve the accuracy of the naive Bayesian classifier（NBC），the selective naive Bayesian（SNB）method and the attributes′prior distribution are studied.Amethod for combining prior distribution and feature selection together is proposed，which finds out the best prior for each attribute after all attributes have been determined by the SNB algorithm.The experimental result on 10 data sets form UCIdata repository shows that thismethod with the general Dirichletprior generally achieves higher classification accuracy，such as the the efficiency of the data sets of Parkinson's can be enhanced by 13.32％.

naive Bayesian classifier；prior distribution；feature selection algorithm；generalized Dirichlet distribution

TP181

A

1001－893X（2013）03－0329－06

10.3969/j.issn.1001－893x.2013.03.020

2012－08－02；

2012－11－12 Received date：2012－08－02；Revised date：2012－11－12

❋❋通讯作者：Jiaopeng－NEAU＠hotmail.com Corresponding author：Jiaopeng－NEAU＠hotmail.com