基于零均值特性的改进G-SVSLMS算法❋

路翠华，谢 鑫，周红梅

（海军航空工程学院7系，山东烟台264001）

基于零均值特性的改进G-SVSLMS算法❋

路翠华❋❋，谢 鑫，周红梅

（海军航空工程学院7系，山东烟台264001）

为解决改进的基于Sigmoid函数变步长最小均方（G-SVSLMS）算法步长更新公式易受噪声干扰的问题，根据高斯白噪声的零均值特性，对G-SVSLMS算法进行改进，提出基于零均值特性的改进G-SVSLMS算法，使算法的抗噪声干扰能力明显增强。理论分析和仿真结果表明：若两算法选取相同参数α、β，则基于零均值特性的改进G-SVSLMS算法相对于G-SVSLMS算法具有小的稳态误差；在保证算法收敛的条件下，基于零均值特性的改进G-SVSLMS算法相对于G-SVSLMS算法具有较快的收敛速度。

信号处理；噪声抑制；G-SVSLMS算法；零均值特性；稳态误差；收敛速度

1 引 言

20世纪60年代初，Windrow和Hoff提出了最小均方误差（LMS）算法。LMS算法计算复杂度低，结构简单，在自适应信号处理领域得到广泛应用。但它的收敛速度慢，收敛速度与自适应步长和失调之间存在着矛盾。针对这个问题，研究人员提出了变步长LMS算法［1－7］。文献［1］介绍了一种基于输出信噪比的滤波算法，若输出的信噪比较小，则增加自适应滤波算法的步长因子，使算法收敛速度加快；反之，减小自适应滤波算法的步长因子，使稳态误差尽量小，但该算法需要预先设置4个参数，参数设置不当会影响算法的性能。文献［2］提出改进的基于Sigmoid函数变步长算法（G-SVSLMS算法），使算法稳态阶段步长因子很小且变化不大，但在对噪声干扰抑制中发现，G-SVSLMS算法步长更新公式易受噪声干扰影响。本文根据噪声干扰的特性对GSVSLMS算法进行改进，假设噪声干扰为高斯白噪声，根据高斯白噪声的零均值特性提出基于零均值特性的改进G-SVSLMS算法。

2 G-SVSLMS算法分析

文献［2］提出的G-SVSLMS算法如下：

式中，参数α＞0控制函数的形状，参数β＞0控制函数的取值范围，μ（n）与α、β和e（n）的关系如图1所示。当α、β选定时，μ（n）由e（n）唯一确定。

图1 μ（n）与e（n）的关系曲线

G-SVSLMS算法具有较快的收敛速度和较小的稳态误差，但在噪声干扰比较严重的环境中，步长更新公式中的e（n）受噪声的影响，使μ（n）不能达到一个很小的值，从而使自适应算法很难达到最优解，只能在最优解附近波动。

3 基于零均值特性的改进G-SVSLMS算法

假设噪声干扰为零均值的高斯白噪声v（n），当滤波器权值ω→ωopt时，e（n）→v（n），E［e（n）］→0，本文对G-SVSLMS算法中的步长更新公式进行改进，用E［e（n）］e（n ）代替公式（2）中的e（n ？，提出基于零均值特性的改进G-SVSLMS算法，其步长更新公式为

假设某时刻ω（n）＝ωopt，此时e（n）＝v（n），GSVSLMS算法的步长更新公式（2）受噪声的影响μ（n）≠0，使ω（n＋1）偏离ωopt，滤波器权值ω（n＋1）在最优权值ωopt附近波动。而当某时刻ω（n）＝ωopt、e（n）＝v（n）时，因噪声干扰为零均值的高斯白噪声v（n），所以E［e（n）］＝0，此时基于零均值特性的改进G-SVSLMS算法的步长μ（n）＝0，权值不再发生改变，保持为最优权值ωopt，所以基于零均值特性的改进G-SVSLMS算法与G-SVSLMS算法相比具有较强的抗噪声干扰能力。

若两算法选取相同参数α、β，则基于零均值特性的改进G-SVSLMS算法相对于G-SVSLMS算法具有小的稳态误差。

证明如下：

设G-SVSLMS算法步长为μ（n），基于零均值特性的改进G-SVSLMS算法步长为μ1（n）。

已知两算法选取相同参数α、β，所以算法开始迭代时，

随着算法趋向于收敛，e（n）→v（n），考虑到高斯白噪声的零均值特性，此时

所以，通常情况下由式（2）、（4）、（7）可得，算法趋向于收敛时

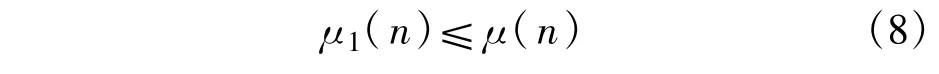
已知小步长LMS算法具有小的稳态误差，大步长LMS算法具有相对较大的稳态误差，所以在选取相同参数α、β的条件下，基于零均值特性的改进GSVSLMS算法相对于G-SVSLMS算法具有小的稳态误差。

证毕。

在保证算法收敛的条件下，若基于零均值特性的改进G-SVSLMS算法和G-SVSLMS算法参数α相同，基于零均值特性的改进G-SVSLMS算法可以选取相对较大的参数β，从而使基于零均值特性的改进G-SVSLMS算法相对G-SVSLMS算法具有较快的收敛速度。

证明如下：

设G-SVSLMS算法的参数为α、β，步长为μ（n），基于零均值特性的改进G-SVSLMS算法的参数为α1、β1，步长为μ1（n），输入信号矢量u（n）相关矩阵为R＝E［u（n）uH（n）］，R的最大特征值为λmax。

由LMS算法均值收敛条件可得，要使GSVSLMS算法和基于零均值特性的改进G-SVSLMS算法收敛，需使

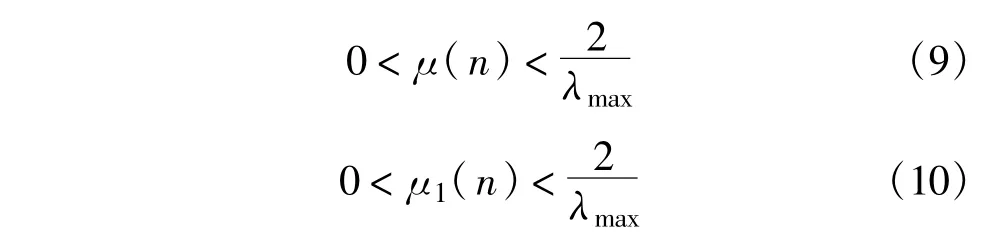
即需使

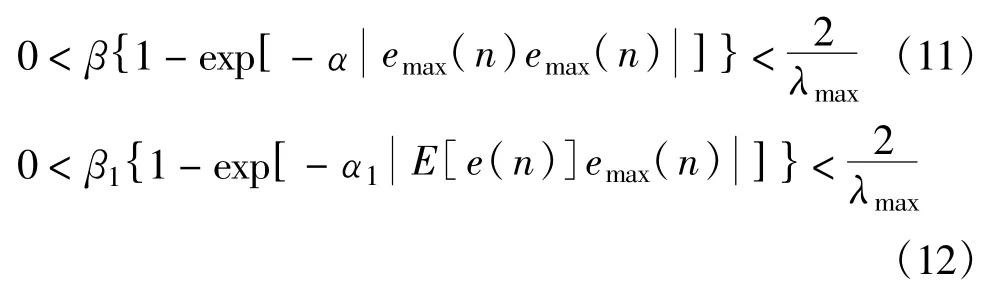
式中，emax（n）为滤波过程中绝对值最大的误差。显然

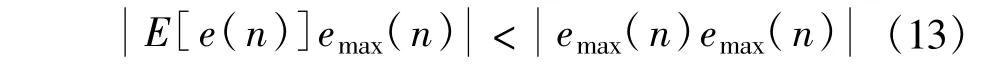
若α＝α1，由式（2）、（4）、（13）可得，满足式（12）的β1可大于满足式（11）的β，即若基于零均值特性的改进G-SVSLMS算法和G-SVSLMS算法参数α相同，基于零均值特性的改进G-SVSLMS算法可以选取相对较大的参数β1，所以基于零均值特性的改进G-SVSLMS算法相对G-SVSLMS算法具有较快的收敛速度。

证毕。

4 仿真分析

下面将基于零均值特性的改进G-SVSLMS算法和G-SVSLMS算法应用到窄带信号的噪声抑制中，通过仿真验证基于零均值特性G-SVSLMS算法的滤波性能。噪声抑制原理如图2所示。

图2 噪声抑制原理

当窄带信号中含有噪声时，由于窄带信号是可预测的，而高斯白噪声的可预测性比较差，可利用其预测性的差异进行噪声抑制。设含有噪声的信号为x，x＝s＋v，其中s为有用信号，v为噪声。因为s为窄带信号，利用预测滤波器可得到信号s的预测信号。误差e＝s＋v－，根据误差e调整滤波器的权值，使→s，从而使e→v，达到噪声干扰抑制的目的。

仿真中选取窄带信号为弹目距离大于3倍脱靶量时连续波多普勒无线电引信回波信号。因仿真中只选取了一小段回波信号，可假设在这一小段时间内回波信号的幅度是不变的。在仿真中，信号s是已知的，用平方误来衡量滤波性能。设弹目相对运动速度为1 000m/s，脱靶量为20m，引信在弹目距离300m时开始工作。引信回波信号SNR＝10 dB，基于零均值特性的改进G-SVSLMS算法和G-SVSLMS算法中参数α＝10、β＝0.4时噪声抑制效果如图3所示，平方误曲线如图4所示。

图3 SNR＝10 dB时噪声抑制效果

图4 SNR＝10 dB、两算法参数相等时平方误差曲线

由图3和图4可以看出，引信回波信号SNR＝10 dB和算法参数α＝10、β＝0.4时，基于零均值特性的改进G-SVSLMS算法收敛速度与G-SVSLMS算法收敛速度基本相等，但其稳态误差明显小于GSVSLMS算法的稳态误差，与前面的理论分析一致。

回波信号SNR＝10 dB和α＝10时，要使GSVSLMS算法的稳态误差与基于零均值特性GSVSLMS算法的稳态误差基本相等，应减少GSVSLMS算法的参数β。G-SVSLMS算法中参数β＝0.01时与基于零均值特性G-SVSLMS算法中参数β＝0.4时收敛后的稳态误差基本相等，此时平方误差曲线如图5所示。

图5 SNR＝10 dB、稳态误差相等时平方误差曲线

由图5可以看出，引信回波信号SNR＝10 dB时，基于零均值特性的改进G-SVSLMS算法具有跟踪缓慢时变信号的能力，在保证两种算法收敛后稳态误差基本相等条件下，基于零均值特性的改进GSVSLMS算法可选取相对较大的参数β，其收敛速度明显快于G-SVSLMS算法，与理论分析一致。

5 结束语

现在LMS算法已经比较成熟，但是结合实际应用可以开展提高其性能的改进算法研究。本文针对G-SVSLMS算法步长更新公式易受噪声干扰的问题，根据高斯白噪声的零均值特性，对G-SVSLMS算法进行改进，提出基于零均值特性的改进G-SVSLMS算法，使算法抗噪声干扰能力增强。该算法可被应用到雷达、无线电引信和通信领域，提高系统的噪声干扰抑制能力。本文算法只适用于均值为0的噪声，对均值不为0的噪声干扰抑制算法有待于进一步研究。

［1］张玲玲，唐晓英，刘伟峰.一种新的变步长LMS自适应滤波算法性能分析［J］.生命科学仪器，2005，3（5）：39－41.ZHANG Ling-ling，TANG Xiao-ying，LIU Wei-feng.Performance analysisofa new variable step size LMSadaptive filtering algorithm［J］.Life Sciences Instruments，2005，3（5）：39－41.（in Chinese）

［2］高鹰，谢胜利.一种变步长LMS自适应滤波算法及分析［J］.电子学报，2001，29（8）：1094－1097.GAOYing，XIE Sheng-li.A variable step size LMS adaptive filtering algorithm and its analysis［J］.Acta Electronica Sinica，2001，29（8）：1094－1097.（in Chinese）

［3］吴光弼，祝琳瑜.一种变步长LMS自适应滤波算法［J］.电子学报，1994，22（1）：55－60.WUGuang-bi，ZHU Lin-yu.A variable step size LMS adaptive filtering algorithm［J］.Acta Electronica Sinica，1994，22（1）：55－60.（in Chinese）

［4］张翔.一种变步长LMS自适应滤波算法研究［J］.航空计算技术，2004，34（1）：9－11.ZHANG Xiang.Study of a variable step size LMS adaptive filtering algorithm［J］.Aeronautical Computer Technique，2004，34（1）：9－11.（in Chinese）

［5］周学文，柯熙政.一种新的变步长LMS自适应滤波算法［J］.西安理工大学学报，2006，22（3）：290－293.ZHOU Xue-wen，KE Xi-zheng.A new variable step size LMS adaptive filtering algorithm［J］.Journal of Xi′an University of Technology，2006，22（3）：290－293.（in Chinese）

［6］Zheng Fanfan，Huang Lianfen，Shi Zhiyuan，et al.Variable Step-size LMS Adaptive Algorithm Based on Computational Verb Rules［C］//Proceedings of 2010 International Conference on Anti-Counterfeiting Security and Identification in Communication.Chengdu：IEEE，2010：343－346.

［7］Lu Cui-hua，Li Guo-lin，Wang Dong-mei.Anti-noise Based on Improved Variable Step Size LMSAdaptive Filtering Algorithm［C］//Proceedings of 2010 International Symposium on Image Analysis＆Signal Processing.［S.l.］：IEEE，2010：82－84.

路翠华（1978—），女，山东烟台人，2011年获博士学位，现为讲师，主要研究方向为自适应信号处理；

LU Cui-hua was born in Yantai，Shandong Province，in 1978.She received the Ph.D.degree in 2011.She is now a lecturer.Her research direction is adaptive signal processing.

Email：llu1978＠163.com

谢鑫（1980—），男，湖北随州人，2010年获博士学位，现为副教授，主要研究方向为阵列信号处理。

XIEXin was born in Suizhou，Hubei Province，in 1980.He received the Ph.D.degree in 2010.He is now an associate professor.His research direction is array signal processing.

Improved G-SVSLMSAlgorithm Based on Zero Mean Characteristics

LU Cui-hua，XIE Xin，ZHOU Hong-mei
（The 7th Department，Naval Aeronautics and Astronautics University，Yantai264001，China）

The G-SVSLMSalgorithm′s step-formula can be disturbed easily by noise jamming.According to the characteristics that themean ofwhite Gaussian noise is zero，improved G-SVSLMSalgorithm based on zeromean characteristics is put forward in order to improved G-SVSLMSalgorithm′s ability of anti-noise.If two algorithms choose the same parametersα，β，improved G-SVSLMS algorithm will have less steady-state error than GSVSLMSalgorithm.Under the condition that the two algorithms are convergent，the convergence rate of improved G-SVSLMSalgorithm is bigger than that of G-SVSLMSalgorithm.Improved G-SVSLMSalgorithm′s performance is testified through theoretical analysis and simulation.

signal processing；noise suppression；G-SVSLMS algorithm；characteristic of zeromean；steady-state error；convergence rate

TN911.72

A

1001－893X（2013）03－0284－04

10.3969/j.issn.1001－893x.2013.03.011

2012－08－21；

2012－12－27 Received date：2012－08－21；Revised date：2012－12－27

❋❋通讯作者：llu1978＠163.com Corresponding author：llu1978＠163.com