一种新的雷达信号旋转干涉仪测向解模糊算法❋
2013-03-24李昀豪
何 明,李昀豪,唐 斌
(电子科技大学电子工程学院,成都611731)
一种新的雷达信号旋转干涉仪测向解模糊算法❋
何 明❋❋,李昀豪,唐 斌
(电子科技大学电子工程学院,成都611731)
研究了一种新的旋转干涉仪测向解模糊算法。首先分析了旋转干涉仪测向时的相位差变化规律,然后针对Ka频段雷达信号在使用旋转干涉仪测向时相位差变化大的问题,建立了进行两次修正的解模糊算法。该方法硬件实现结构简单,易应用于被动导引头中。通过计算机仿真验证算法的稳定性,结果表明,当信噪比高于-8 dB时,解模糊成功率超过90%。
Ka频段雷达信号;旋转式干涉仪;测向;解模糊;被动导引头
1 引 言
干涉仪测向系统及其各种改进方式已广泛应用于被动雷达测向领域[1],并且二维多基线干涉仪可同时测量方向角与俯仰角[2]。随着现代雷达技术的逐步发展,Ka频段的雷达信号越来越多地出现在电子对抗环境中,随之而来的是更多高次模糊相位差值,导致常规的干涉仪测向体制在这样的环境中难以较好地完成测向解模糊。文献[3]用数字积分器原理进行测向解模糊,但难以应对相邻脉冲到达干涉仪相位差变化超过2π情况。文献[4]基于半圆阵任意基线,研究了多组模糊集求交集的解模糊算法,具有系统原理简单以及天线布局灵活等优点,但其多接收通道结构会增加系统体积和功耗等。
针对现有干涉仪测向系统及其算法局限性,本文以旋转干涉仪体制为基础,研究了一种采用数字积分器进行第一次模糊修正,判别数字积分结果是否存在二阶差分突变而进行第二次修正的算法。仿真结果表明,该算法具有较高的解模糊成功率。
2 信号模型
图1中,干涉仪AB基线在XOY平面上旋转,距离为d,信号波长为λ。直线l为目标视线,其与Z轴夹角为β,0≤β<π/2,视线l在XOY面上的投影与X轴正方向夹角为α,α∈[0,2π),干涉仪转角速度为ω,基线初始位置为X轴(A正轴、B负轴),则两接收天线分别位于A、B两点时,第n(n=1,2,…,N)个脉冲到达时两天线之间的相位差为

其中,Δt为雷达脉冲到达时间间隔(PRI),以第一个脉冲到达时间作为起始零时刻;β的范围一般为(0°,40°)[5];由于脉冲到达时间间隔相对于弹旋周期很短,因此认为α、β为常量,式(1)表明旋转式干涉仪相位差在短时间内变化只随脉冲到达时间呈正弦规律;Ka频段信号波长λ范围为[8.33,8.98]mm。假设干涉仪旋转角速度ω=20πrad/s,基线长度d=150mm,则当β=π/6时,|φ(n)|≤π。由于实际求出的?(n)∈(-π,π),故φAB存在周期模糊,且有
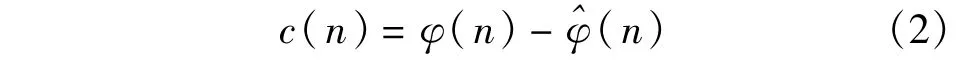
式中,c(n)为2π的整数倍。

图1 待测角与弹体坐标关系
3 解模糊原理
目标雷达信号脉冲重复频率(PRF)为20 kHz时,有

上述参数条件下,|Δφ(n)|≤0.09π。故可通过数字积分器对模糊相位进行积分[1],引入修正序列c′(n)。数字积分器原理如式(4):
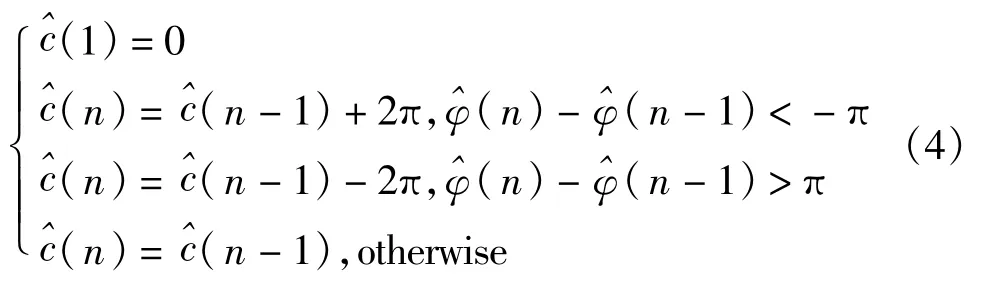
于是,有

通过该方法,可正确地实现信号的解模糊,如图2所示。仿真中信号载频为36 GHz。但是,由于(1)∈(-π,π),而φ(1)∈[-18π,18π],故(1)与φ(1)不一致,导致(n)与φ(n)相差一直流U。

图2 模糊相位差及数字积分输出
由于毫米波频段雷达信号波长较小,所以旋转式干涉仪接收到的两通道相位差变化范围很大,特别是当目标雷达信号脉冲重复频率(PRF)相对较低时,两相邻脉到达时间间隔较大,或者干涉仪基线旋转速度较快时,相邻到达脉冲干涉仪相位差变化Δφ(n)有可能超过π,即会出现周期模糊区域,数字积分器失效。例如,其他参数同前,目标雷达信号PRF由20 kHz降低为1 kHz,干涉仪旋转角速度ω提高到30πrad/s时,max(Δφ(n ))≈1.70π。模糊相位差及数字积分器输出结果如图3所示。

图3 错误的数字积分结果
在一个基线旋转周期中,数字积分器在相位变化较大的部分无法得到理想输出。但是,在相位差变化正弦曲线波峰和波谷位置及其邻近部分,相邻脉冲到达时相位差变化仍然不超过π,数字积分器的输出仍然正确。当数字积分器输出错误时,其输出结果的二阶差分值(n)会出现突变,如图4所示。

图4 相位差二阶差分
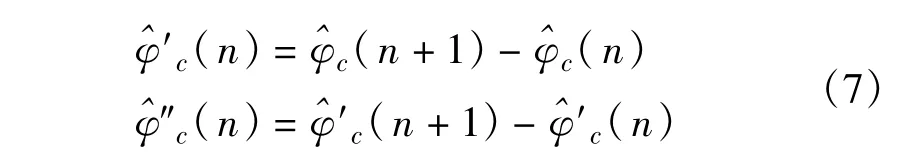
判断是否存在差分突变就可以找到数字积分器错误输出,并依此对数字积分器输出c(n)进行第二次修正。从波峰(波谷)位置向后进行第二次修正具体步骤如下。


并从P点开始第二次修正,p=P。

从序号P至N脉冲的模糊相位差第二次修正完成后,从P-1至起序号为1的第二次修正与上述过程原理完全一样。从波峰位置开始进行第二次修后的结果如图5所示。
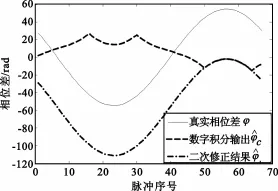
图5 完成二次修正后的相位差
完成整个基线旋转周期的二次修正后,为了消除直流分量,减去相位差均值,就可以得到无模糊的相位差。突变门限Thφ设定视具体实际而定。不难得到结论,受噪声对测向精度的影响,Th稍大于可能出现的最大相位二阶差分值即可。
4 相位测量及算法仿真
4.1 相位测量
旋转干涉仪接收及信号处理系统结构如图6所示,两天线接收到射频信号后由射频前端下变频输出中频信号。为保证两接收通道ADC采样在时间上同步,采用单片双通道ADC芯片,其两通道的采样时间由同一时钟源提供。

图6 系统实现框图
设A、B两通道的离散复信号为

其中,vA(n)、vB(n)都是零均值的高斯白噪声。
对sA(n)和sB(n)进行DFT,可得


其中,k=0,1,2,…,N-1,N为信号采样点数。两通道的初相信息包含在SA(k)、SB(k)中信号的DFT部分。若令m=m′+Δm=π,其中m′为整数,Δm为绝对值小于1的实数,且S1(m′)为S1(k )中的最大项。将m′代入前面两式的第一求和项中,有

其中:

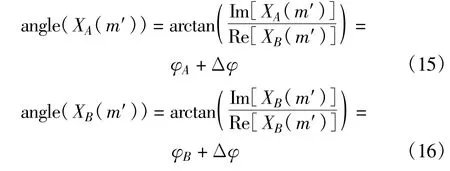
上式无法准确求出两通道各自的信号初始相位,但是可以计算出它的相位差

4.2 计算机仿真
为了验证上述解模糊算法的有效性,进行了如下仿真。仿真中,图1模型中的β在0~π/6内随机取值,α在0~2π内随机取值,信号PRF为0.5kHz,中频频率为100MHz,脉冲宽度为5μs,基线长度d=150mm,射频波长λ=8.33mm。针对不同采样频率和不同中频信号信噪比分别进行500次Monte-Carlo实验,得出如图7所示的结果。

图7 解模糊成功率仿真结果
从图7看出,信噪比相同时,解模糊成功率随数字化采样频率的提高而提高。同样,当采样频率相同时,解模糊成功率也随信噪比的提高而提高。这都是相位测量精度受采样速率及信噪比影响的直接体现,和文献[6]对测量精度的分析结果相同。仿真表明,当数字化采样频率高于信号频率3倍、信噪比优于-8dB时,解模糊成功率超过90%;而数字化采样频率高于信号频率7倍、信噪比优于-10dB时,解模糊成功率超过90%。另外,仿真用到的信噪比参数是中频信号的,在工程实际中,通过数字信道化等措施提升信噪比可进一步提高解模糊成功率。
5 结论
本文研究了Ka频段雷达信号旋转干涉仪测向解模糊算法,解决了单基线测向模糊问题。结合超外差式接收机及高速数字信号处理芯片使用,可以实现厘米频段和毫米频段的雷达辐射源空间定位。其旋转式单基线结构与多基线体制相比较,接收通道数减少、系统结构简化以及功耗降低,利于在被动雷达导引头中应用。与已经发表的研究成果相比,本文采用数字积分修正的方法,将复杂的多通道结构转换成了数值计算。在对原理样机的测试过程中发现,实际结果与理论预期基本相符,未产生例外情况。鉴于信噪比对系统结果有较大影响,在进一步的研究中,建议采用稳健高概率的信号检测与参数估计技术来提升解模糊的成功率。
[1]司锡才,赵建民.宽频带反辐射导弹导引头技术基础[M].哈尔滨:哈尔滨工程大学出版社,1996:77-83.SIXi-cai.Broadbandanti-radiationmissileseekertechnology[M].Harbin:HarbinEngineeringUniversityPress,1996:77-83.(inChinese)
[2]肖秀丽.干涉仪测向原理[J].中国无线电,2006(5):43-49.XIAOXiu-li.Theprincipleoftheinterferometer[J].ChinaRadio,2006(5):43-49.(in Chinese)
[3]司伟建,程伟.旋转干涉仪解模糊方法研究及实现[J].弹箭与制导学报,2010,30(3):199-202.SI Wei-jian,CHENG Wei.Study on Solving Ambiguity Method of Rolling Interferometer and Implemention[J].Journal of Projectiles,Rockets,Missiles and Guidance,2010,30(3):199-202.(in Chinese)
[4]司伟建,初萍,孙圣和.基于半圆阵的解模糊技术研究[J].系统工程与电子技术,2008,30(11):2128-2131.SIWei-jian,CHU Ping,SUN Sheng-he.Research on solving ambiguity technology based on semi-circle array[J].Systems Engineering and Electronics,2008,30(11):2128-2131.(in Chinese)
[5]司伟建.反辐射导弹抗多点源技术研究[D].哈尔滨:哈尔滨工程大学,2004.SIWei-jian.Anti-radiation missile anti-multi-point source[D].Harbin:Harbin Engineering University,2004.(in Chinese)
[6]孔德强,刘作学,田战丽.干涉仪相位差抖动分析[J].兵工自动化,2010,29(1):77-79.KONG De-qiang,LIU Zuo-xue,TIAN Zhan-li.Analysis on Interferometer Phase Difference Vibration[J].Ordnance Industry Automation,2010,29(1):77-79.(in Chinese)

何明(1987—),男,山东人,2010年于电子科技大学获工学学士学位,现为硕士研究生,主要研究方向为高速数据采集与处理;
HEMing was born in Shandong Province,in 1987.He received the B.S.degree in 2010.He is now a graduate student.His research direction is high speed data acquisition and processing.
Email:892560569@qq.com
李匀豪(1987—),男,四川人,2009年于西安电子科技大学获工学学士学位,现为博士研究生;
LIJun-haowas born in Sichuan Province,in 1987.He received the B.S.degree from Xidian University in 2009.He is currently working toward the Ph.D.degree.
唐斌(1964—),男,四川广安人,教授、博士生导师,主要从事电子对抗、雷达抗干扰和新一代通信技术方面的研究。
TANG Binwasborn in Guang′an,Sichuan Province,in 1964.He is now a professor and also the Ph.D.supervisor.His research interests include electronic countermeasure,radar anti-jamming technology and new-generation communication technology.
Email:bint@ee.uestc.edu.cn
A New Method for Ambiguity Solving Based on Rotary Interferometer
HEMing,LIYun-hao,TANG Bin
(School of Electronic Engineering,University of Electronic Science and Technology of China,Chengdu 611731,China)
Based on rotary interferometer,an approach for phase differencemeasurementand ambiguity solving is presented.First the changes of phase difference are analyzed when using a rotating interferometer to find direction,then aiming at the problem that for Ka-band radar signals the phase difference becomes greaterwhen using a rotating interferometer to find direction,twicemodified ambiguity solving algorithm is established.Adopting thismethod,the hardware structure is easy to be achieved in the passive seeker.According to the simulation result,probability of ambiguity solving is better than 90%when SNR(Signal-to-Noise Ratio)is above-8 dB.
Ka-band radar signal;rotary interferometer;direction finding;ambiguity solving;passive seeker
TN971.1
A
1001-893X(2013)03-0297-05
10.3969/j.issn.1001-893x.2013.03.014
2012-10-22;
2013-01-21 Received date:2012-10-22;Revised date:2013-01-21
❋❋通讯作者:892560569@qq.com Corresponding author:892560569@qq.com
