混合场积分方程在开放结构散射分析中的应用

巩 强，陈佳林，王 旻，李 睿，张 军，李相平

（1.海军驻成都地区军事代表室，成都610036；2.海军航空工程学院a.电子信息工程系；b.兵器科学与技术系，山东烟台264001）

矩量法（Method of Moments，MoM）作为一种精确的积分类数值方法，具有严格的理论模型，格林函数的引入使其积分方程自动满足无穷远处的辐射边界条件，能精确模拟电磁波传播的索末菲辐射条件，非常适合求解开域问题，如电磁辐射和散射问题[1-6]。

对于金属目标的电磁散射问题，表面积分方程的建立可以采用电场积分方程（Electric Field Integral Equation，EFIE）[7]、磁场积分方程（Magnetic Field Integral Equation，MFIE）或混合场积分方程（Combined Field Integral Equation，CFIE）[8]。EFIE可用于闭合金属面问题，亦可用于开放金属面问题，相对于MFIE和CFIE，其离散后的系数矩阵条件数最大，迭代求解时收敛速度最慢。MFIE只能用于闭合金属面问题的分析，其系数矩阵条件数小于EFIE，但大于CFIE。CFIE是EFIE和MFIE的线性组合，由于其中包含了MFIE，故只能用于闭合金属面问题的分析，其系数矩阵的条件数最小，迭代求解时收敛速度最快。

然而，在实际的目标环境电磁仿真模型中，出现了大量的复合结构，比如，导弹中的弹体和弹翼、目标与粗糙面复合散射问题中的三维闭合目标和二维粗糙面等，这类结构模型由部分开放表面和部分闭合表面组成，作为一个整体，该结构仍然是开放结构，这不可避免地只能在目标表面建立EFIE。采用EFIE所形成矩阵方程的系数矩阵条件数较大，迭代求解时收敛效率低，引入各种快速算法固然可以有效地提高求解效率，诸如快速傅里叶变换（Fast Fourier Transform，FFT）技术、多层快速多级子方法（Multilevel Fast Multipole Algorithm，MLFMA）[9-10]等，但对于电尺寸较大的目标而言，仍然会面临收敛效率低，甚至不收敛的问题。而CFIE 只能用于分析闭合结构，故不能直接在该复合目标表面建立CFIE，其优势很难在这种复合结构上发挥作用。

本文针对复合开放闭合结构的电磁散射问题，通过修改CFIE的建立方式，将CFIE 扩展应用到了开放结构，大大提高了迭代效率。

1 理论推导

对于金属导体表面，EFIE 和MFIE的矩量法求解所形成的矩阵方程组可表示为：

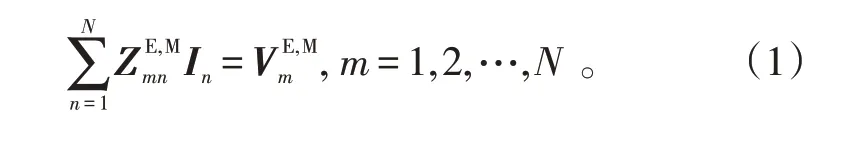
式（1）中：

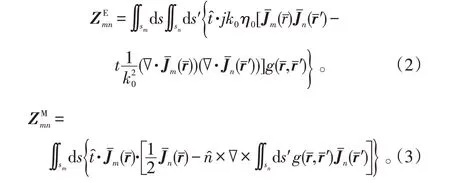
右边向量的表达形式如下：

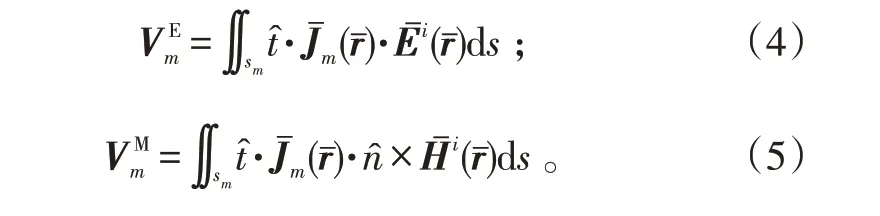
式（1）～（5）中：k0和η0分别表示自由空间的波数和波阻抗表示自由空间的格林函数；r和r′分别表示场点和源点的位置表示目标表面的单位切向量是入射电场是入射磁场；Zmn是阻抗矩阵；In是需要求解的未知系数；Vm是包含入射波信息的激励向量。

CFIE是EFIE和MFIE的线性组合，矩阵方程的系数矩阵为

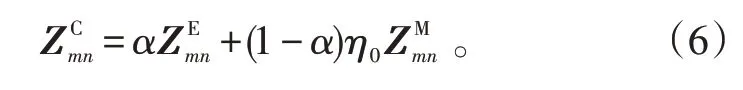
式（6）中，α和(1-α)分别表示EFIE 和MFIE 在CFIE 中的权重。对于传统的CFIE，α取一个常数，且0＜α＜1，只能用于闭合结构电磁散射问题的求解，这种设置α的方式严重限制了CFIE的应用范围。

对于复合开放闭合结构，本文的主要思想是将α设置为一个灵活的变量αm、αm仍然满足0＜αm＜1。这样，对于不同的测试函数可以选择不同的线性组合。修改后的CFIE的建立方式可以用式（7）表示，

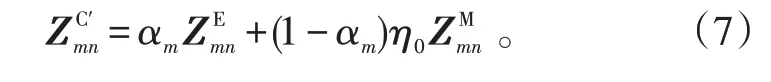
对复合结构中闭合区域上的测试函数，取αm≠0，使用CFIE，其中不同的m值对应的αm可不同，对复合结构中开放区域上的测试函数，取αm=1，使用EFIE，便把CFIE引入到开放结构问题的求解。将α设为αm，使EFIE 和MFIE 在CFIE 中的权重是可灵活变化的，这样可以有效地改善矩阵性态，提高迭代求解效率。

2 数值算例

为了验证该算法的有效性，本文分析了3种复合结构的电磁散射问题。目标表面采用三角形进行离散，基函数选择RWG 基函数并采用Galerkin’s 测试，所形成矩阵方程的迭代求解采用一般最小余量法（Generalized Minimal Residual，GMRES），并引入多层快速多级子方法（Multilevel Fast Multipole Algorithm，MLFMA）来加速矩阵矢量乘。

算例1：球体和矩形平面复合结构，剖面图如图1所示。球体半径为2 m，矩形平面长和宽皆为1 m，球体和平面的距离为3 m，离散后闭合区域和开放区域的RWG单元个数分别为15 921和313，入射平面波频率f=300 MHz，入射方向为θ=0、φ=0。仿真的雷达散射面积（RCS）结果如图2所示。

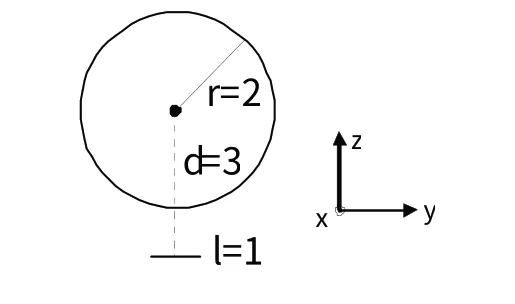
图1 三维复合结构的剖面图

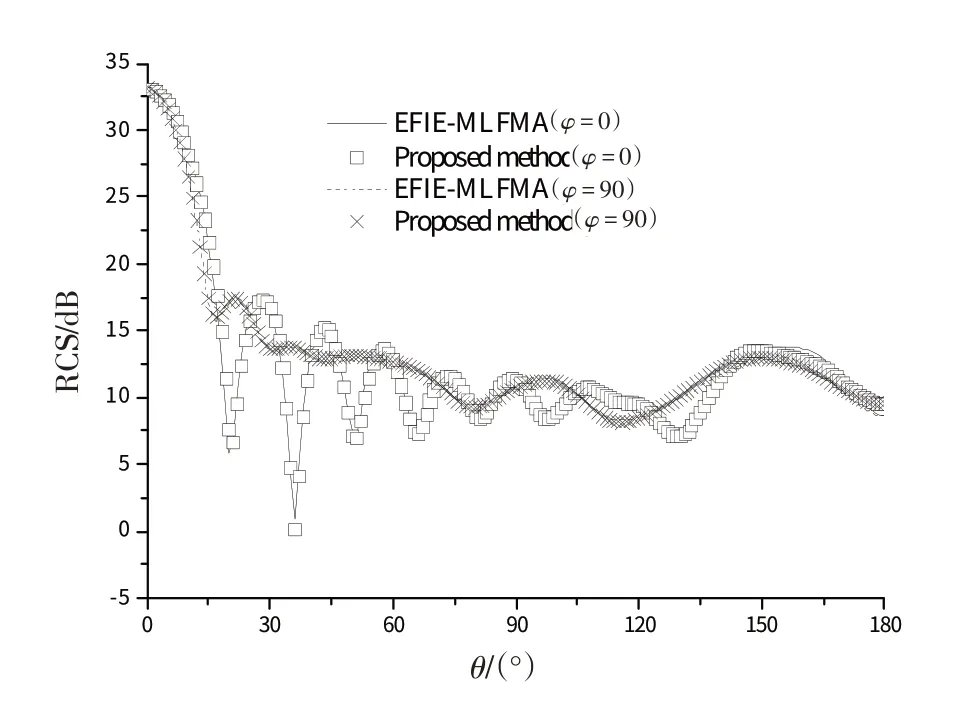
图2 球体和矩形平面复合结构仿真RCS结果

迭代步数和迭代时间在表1中列出。

表1 迭代步数和迭代时间比较

由图2所示的仿真结果可看出，本文提出的方法与传统的EFIE方法的计算结果吻合，验证了方法的准确性。从表1可看出，该方法有效地提高了求解效率。

算例2：人造卫星结构，该结构是立方体和矩形平面的复合结构。立方体边长为1 m，矩形平面长5 m，宽0.5 m，卫星结构图如图3所示。离散后闭合区域和开放区域的RWG[7]单元个数分别为5 670 和4 326，入射平面波频率f=300 MHz，入射方向为θ=0、φ=0。仿真的RCS见图4，2种方法的计算结果吻合良好。

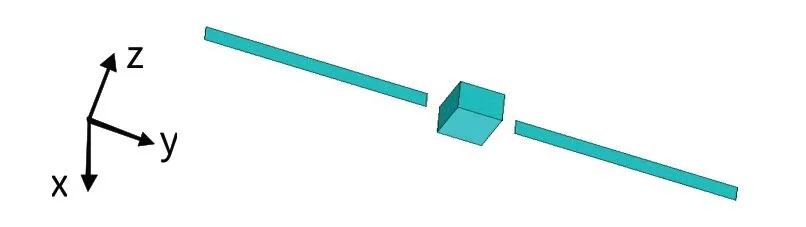
图3 人造卫星结构图

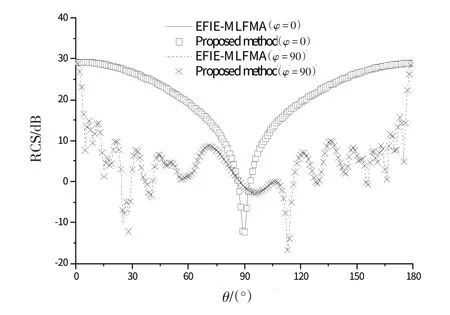
图4 人造卫星仿真RCS结果

由于该复合结构开放区域较大，只在立方体表面建立了CFIE，因而矩阵方程求解的迭代步数仅从404降低到310，没有算例1降低得显著。

算例3：一个简易的导弹模型，导弹模型由弹体和弹翼组成，其中弹体由半球体和圆柱体组成，弹翼为2个矩形平面，半球体的半径为0.5 m，圆柱的半径为0.5 m，高为8 m，矩形平面的长为0.5 m，宽为0.5 m，模型的离散结构图如图5所示。离散后闭合区域和开放区域的RWG 单元个数分别为8 979 和154，入射平面波频率f=300 MHz，入射方向为θ=0、φ=0。仿真的RCS结果如图6所示，2种方法的计算结果吻合良好，迭代步数和迭代时间在表2中列出，迭代步数和迭代时间降低显著。

图5 导弹模型的离散结构图

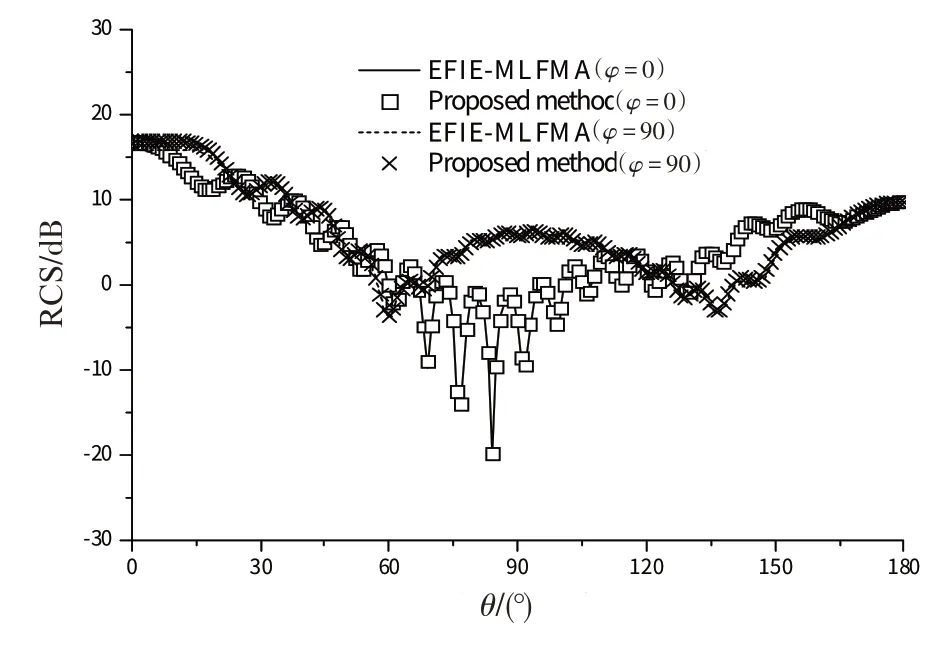
图6 简易导弹模型仿真RCS结果

表2 迭代步数和迭代时间比较

3 结束语

通过修改混合场积分方程的建立方式，将混合场积分方程引入复合开放闭合目标电磁散射问题的求解，拓展了混合场积分方程的应用范围，有效地改善了求解效率，特别是对于开放区域较小的结构，效果尤其显著，数值算例证明了该方法的精度和效率。

[1]MICHALSKI K A，ZHENG D L.Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media，part I：theory[J].IEEE Transactions Antennas and Propagate，1990，38（3）：335-344.

[2]MICHALSKI K A，ZHENG D L.Electromagnetic scattering and radiation by surfaces of arbitrary shape in layered media，part II：implementation and results for contiguous half-spaces[J].IEEE Transactions Antennas Propagate，1990，38（3）：345-352.

[3]COIFMAN R，ROKHLIN V，WANDZURA S M.The fast multipole method for the wave equation：A pedestrian prescription[J].IEEE Transactions Antennas Propagate，1993，35（3）：7-12.

[4]LU C C，CHEW W C.A multilevel algorithm for solving boundary integral equations of wave scattering[J].Microwave Optic Technology Letter，1994，7：466-470.

[5]CHEN JIALIN，LI SHANGSHENG，WANG MIN.Targets identification method based on electromagnetic scattering analysis[C]//2011 IEEE CIE International Conference on Radar.2011：1647-1651.

[6]CHEN JIALIN，LI SHANGSHENG，SONG YAPING.Analysis of electromagnetic scattering problems by means of a VSIE-ODDM-MLFMA method[J].Applied Computational Electromagnetic Society Journal，2012，27（8）：660-667.

[7]RAO S M，WILTON D R，GLISSON A W.Electromagnetic scattering by surface of arbitrary shape[J].IEEE Transactions Antennas Propagate，1982，30（3）：409-418.

[8]SONG J M，CHEW W C.Multilevel fast-multipole algorithm for solving combined field integral equation of electromagnetic scattering[J].Microwave Optic Technology Letter，1995（10）：14-19.

[9]ENGHETA N，MURPHY W D，ROKHLIN V，et al.The fast multipole method（FMM）for electromagnetic scattering problem[J].IEEE Transactions Antennas Propagate，1992，40（6）：634-641.

[10]SONG J M，LU C C，CHEW W C.Multilevel fast multipole algorithm for electromagnetic scattering by large complex objects[J].IEEE Transactions Antennas Propagate，1997，45（10）：1488-1493.