张拉结构风致振动理论和试验研究
2013-03-23张其林闫雁军
张其林 闫雁军 李 晗
(同济大学建筑工程系, 上海 200092)
张拉结构具有质量轻、刚度柔、阻尼小等特点,风荷载作用下,维护结构易发生振动,可能引发局部撕裂或破坏,甚至导致主体结构失效.对风致振动的研究已有很多,大部分集中在大跨桥梁和高层建筑[1-6].对于大跨张拉结构的研究工作相对滞后,研究成果较少,目前尚没有成熟的抗风设计方法.本文采用风洞试验、FSI数值模拟方法和基于随机振动理论的频域方法,对结构风致振动响应结果进行了分析比较,验证了理论方法的可靠性.
1 结构风致振动响应
1.1 流固耦合数值模拟理论
流固耦合(FSI)是研究变形固体在流场作用下的各种行为以及固体位形与流场分布之间相互作用的一门交叉学科.流固耦合的一个重要特征是流体与固体两相介质的相互作用,固体在流体作用下发生变形、运动;固体变形或运动反过来又影响流体流动,从而改变流体载荷的分布和大小.
耦合问题的整体方程可表示为
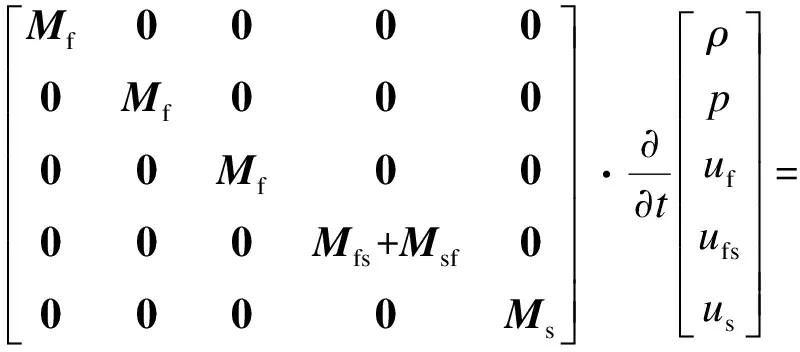
(1)
式中,Ms,Mf分别为结构质量矩阵和荷载质量矩阵;Mfs,Msf分别为流固耦合界面上固体和流体的质量;ρ,p,uf,us,ufs分别为流体的密度、压力、流体速度、结构速度和流固耦合面速度;fρ,fp,fu分别为流体的密度向量、压力向量和速度矢量;fufs和fusf分别为流固耦合面上分别作用在流体和固体表面的荷载矢量;fs为作用在结构上的荷载矢量;L为荷载矩阵;σfs为界面上的流体荷载.
流固耦合方程求解方法主要分为2大类[7]:① 直接耦合算法(direct coupling method).该算法将结构、流场、耦合界面的物理量统一在一个方程组里进行直接求解,适用性宽泛,但由于计算需求庞大,发展比较缓慢.② 迭代耦合算法(iterative coupling method),又称为分离式算法(partitioned method).其基本思想是流场、固体在各自的CFD和CSD程序中,通过流固耦合界面,完成双向数据传递、交替更新,直至达到收敛.本文采用迭代耦合算法.
由于流体方程是非线性的,流固耦合方程也具有非线性特性.求解方程的过程实质上是一个反复迭代逼近真实解的过程.在迭代过程中,需要设立应力准则或位移准则来判断是否收敛,即

(2)

(3)
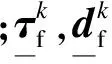
1.2 频域法的基本理论
依据随机振动理论,结构在平稳随机脉动风荷载作用下的动力方程为
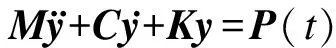
(4)

(5)

采用振型分解法对方程(4)进行解耦,可得广义坐标下的运动方程为
(6)
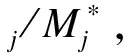
求解结构的脉动响应可转换为求解脉动位移根方差,具体步骤如下:
① 计算节点广义荷载谱.依据随机振动理论,可得脉动风压荷载谱Spp和广义荷载谱Sfjfk间的关系式为

(7)
空间中任意2点w,q间的脉动风压荷载互谱为

(8)
式中,coh(r,n)为空间相干函数;r为2点间距离;Spw(n)和Spq(n)分别为节点w和q的脉动风压谱.
② 依据广义荷载,计算广义坐标功率谱.第k阶和第j阶模态响应的互功率谱为
(9)
式中,Hj(n)为第j阶模态的频响函数.
③ 计算结构响应功率谱.节点i处的动力位移响应根方差σyi为

(10)
式中,φji为节点i的第j阶振型位移值.
式(10)中包含了所有参振模态交叉项,计算量大,计算效率低.随着结构节点数目的增加,与振型分解组合法(SRSS)计算方法相比,CQC的计算耗时呈指数型增长.因此,目前大多采用SRSS法,具体表达式为

(11)
作用在结构上的风荷载可以分为平均风荷载和脉动风荷载2个部分.在平均风荷载作用下,结构变形到达新平衡位置,结构刚度和频率随之改变.风荷载作用下,结构在新平衡位置随机振动,刚度近似不变,根据式(11),可以计算得到结构脉动响应.
式(11)可转化为

(12)
式(12)中等式右边第1部分可记为背景分量σB,第2部分记为共振分量σR,即
(13)
(14)
定义共振分量占总风致响应的比值为
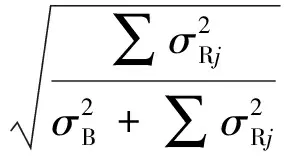
(15)
评价各阶模态对结构响应贡献的大小,可根据各振型响应的应变能在结构总应变能中所占比例来衡量[8].实际计算中,通常考虑有限阶计算振型,通过下式计算各振型应变能比例,衡量计算振型对结构响应贡献的大小:
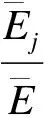
(16)

1.3 风洞试验
风洞试验不仅可以测试刚性建筑表面的风压和体型系数,对桥梁、高层等结构风致振动的测试也很有效.张拉结构动力相似准则在风洞试验中难以满足,本文中风洞试验仅用于模型本身的风致振动特性研究,同时为FSI数值模拟分析和频域法分析结果的正确性提供必要的佐证.
2 单片索膜风致振动
在风洞中,对边长为1m的方形索膜进行气弹模型试验.膜材选择702 Fluotop T2,厚度为0.52mm,密度为750g/m2,经向、纬向抗拉强度分别为3000N/5cm,2800N/5cm,经向弹性模量为558MPa,纬向弹性模量为521MPa.试验流场选择均匀紊流场,紊流强度为14%.风速选取为10,16,22m/s.膜表面预张力选取为0.75,1.50,2.25,3.00kN/m.分别对膜面测点的位移和加速度进行测量.图1为试验测点布置及试验现场照片.

图1 单片索膜气弹风洞试验
采用移动锤击跑点法,根据测点加速度时程信号识别膜片振动特性.倾角α=45°的张拉膜在4个预应力水平下,不同测点识别出的前5阶频率结果见表1.

表1 不同预张力膜结构频率(α=45°) Hz
当风速为22m/s、膜面倾角α=45°时,不同预张力水平下膜面测点的平均位移和根方差见图2.由图可知,随着预张力水平的下降,张拉膜面各测点的位移均值呈非线性增加,且增加幅度逐渐变大.位移根方差则随预张力水平降低而逐渐增大.

图2 测点位移均值及根方差随预张力的变化曲线
膜结构振动与周围气体形成的耦合效应会产生附加质量,影响结构动力特性参数的求解.考虑空气,建立势流体流固耦合的计算模型(见图3).
图3 单片索膜势流体模型
当膜面倾角α=45°、预张力为2.24kN/m时,索膜结构数值模型频率的计算结果见表2.由于结构振动模态较为密集,扣除重根,计算值与试验结果较为吻合.

表2 索膜结构频率试验的识别及数值计算结果 Hz
当风速为16m/s、膜面倾角α=45°、膜面预张力为2.24kN/m时,测点D3的试验平均值为11.0mm,位移根方差为0.86mm.提取结构模型测点D3的位移时程曲线,结果见图4.数值计算测点D3的位移均值为11.2mm,位移根方差为0.81mm,这与试验结果基本吻合.

图4 测点D3数值模拟位移时程
根据风速16m/s时的测点位移、加速度时程曲线,通过FFT变化得位移功率谱(见图5)和加速度功率谱(见图6).位移谱可以体现出结构振动的低频部分,而加速度谱则体现出结构振动的高频部分.由位移时程曲线及自功率谱曲线可以看出,结构的振动频率包含2个部分,一部分为风荷载的频率成分,另一部分为结构自身固有的频率成分.结构以比其自振频率低得多的频率做随机振动,振动形式主要为脉动风引起的强迫振动.而加速度反应谱表明结构的振动是一个宽带过程,脉动风场会激起结构的某些振型.

图5 测点D3的位移时程及功率谱(v=16m/s)
采用单向流固耦合方法,计算结构的风致动力响应.先将流场中膜结构表面设置为固壁,进行钝体绕流的瞬态分析,获取结构表面的风压,存储到文件中.然后,在结构表面对应的节点上,完成膜结构在风压作用下的隐式动力分析.
在风速为16m/s、膜面预张力为2.24kN/m、膜面倾角α=45°的工况下,利用FSI计算单向耦合和双向耦合并对比其区别.由图7可知,2种方法得到的结构响应差异很小,这主要是因为结构体型较为简单,膜结构预张力较大,风作用下膜结构表面变形较小,结构表面的风压分布主要受到结构宏观尺寸的影响,局部形状的变化对大尺度涡的影响较小.

图6 测点D3的加速度时程及功率谱(v=16m/s)

图7 单向耦合与双向耦合比较
采用频域法计算单片索膜脉动位移.由公式y=μσy计算脉动位移峰值,其中μ=2.2为保证系数,结果见图8.脉动位移峰值最大为1.94mm,对应位移根方差为0.88mm,计算结果与试验结果(见图4)接近.第1阶模态所占振型能量比较大,达到98%.共振分量占脉动位移百分数约为16%.结合图5可知,脉动响应以背景分量为主.

图8 频域法计算结果
3 平面索网风致振动
图9为一单层平面索网,高24.64m,宽26m,作为玻璃幕墙的支撑体系,位于宜兴东氿大厦入口.玻璃采用8mm+8mm的双层夹胶玻璃,分格列数为17,行数为16.第1列和最后1列的分格尺寸为1750mm×1540mm,中间部分的分格尺寸为1500mm×1540mm.

图9 东氿大厦及平面索网测点布置
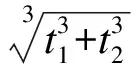
建立了包含玻璃面板、索网、爪件、密封胶在内的玻璃-索网结构整体计算模型.在基本风压w0=450Pa作用下,索网玻璃幕墙的最大静力位移为0.1621m.对结构进行模态分析,频率计算结果见表3.

表3 索网幕墙前8阶频率和周期
考虑玻璃幕墙及S形裙房,建立流场,流体模型网格划分结果见图10,单元数为8.4×105,节点数为4.1×105.

图10 流场网格划分示意图
结合CSD和CFD模型,进行00风向角(即来流方向与玻璃面板垂直)流固耦合计算.采用AR模型生成脉动风速,模型阶数P=4,目标谱采用湍流尺度沿高度不变的Davenport风速谱,按照基本风压换算成平均风速为27m/s的脉动风速时程,入口风速剖面沿高度不变.截取60s风速时程施加在风速入口(见图11),玻璃面板设置为流固耦合面.

图11 入口风速时程及功率谱
在玻璃面板上布置9个测点(见图9),提取测点位移和压力时程,进行统计分析,相关结果见表4.平均位移最大值为0.156m,位于玻璃面板中部;在基本风压为w0=450N/m2的荷载作用下,结构最大静力位移为0.162m.这二者基本相等.
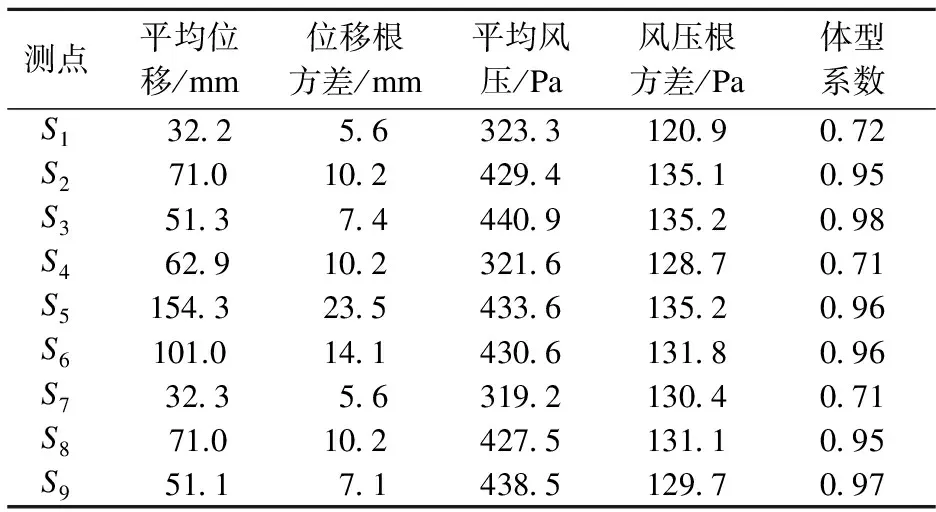
表4 测点位移及风压流固耦合结果
图12为测点S5的位移、加速度和节点压力时程,图13为频域分析得到的位移幅值谱和加速度功率谱.由图12可知,在脉动风荷载作用下,索网幕墙主要做受迫振动,以背景响应为主,共振响应比重较大.由图13可知,在脉动风作用下,结构的前几阶模态被激发出来,振动为窄带过程.

图12 测点S5的位移、加速度和节点压力时程曲线

图13 测点S5的位移、加速度功率谱
忽略玻璃玻璃面板,对单层索网进行频域法分析,索网位移根方差最大值为54mm,位于索网中部.脉动位移峰值见图14,最大值为118.8mm.第1阶模态所占的振型能量比较大,达到87.3%;索网中部共振分量占脉动位移的百分数约为30%,共振响应比重较大,这与图13的结论相同.

图14 频域法计算结果
4 膜结构屋盖风振响应
如图15所示,选择世博轴1号阳光谷和2号阳光谷及其之间的膜结构,建立1∶40气弹模型试验,平面尺寸为5.812 m×3.044 m.

图15 膜结果平面图和试验模型
风洞试验时,来流分为均匀来流和模拟C类地貌的紊流.通过栅栏、尖劈和粗糙元模拟了C类地貌的边界层风速剖面和湍流度.
试验位移和加速度测点布置如图 16所示.不同的风向、预张力水平、风速和来流的试验工况列于表5.

图16 试验测点布置图

表5 试验工况
根据风洞测点加速度时程数据,采用随机子空间法识别低预应力膜结构频率,结果见表6.根据风洞模型,建立包括膜面及其支撑系统的数值模型,将计算频率与识别频率对比可知,数值模型基本反映了结构的自振特性.
在均匀流、v=10m/s、α=0°、低膜面应力的工况下,膜面测点1、2、7、8的位移和加速度时程见图17和图18.

表6 数值模拟及风洞识别频率 Hz

图17 位移时程(均匀流,v=10m/s,α=0o,低膜面应力)
由于膜结构的空间造型比较复杂,均匀来流受建筑物干扰形成特征湍流,引起膜面振动.对测点位移时程和加速度时程进行功率谱分析,结果见图19和图20.由图19可知,结构振动主要以低频部分为主,做受迫振动.由图20可知,结构振动是一个宽带过程,某些振型会被脉动风激发出来.
采用混合网格建立CFD模型,单元数为660690,节点数为240761.图21为结构及流域网格划分示意图.

图18 加速度时程(均匀流,v=10m/s,α=0o,低膜面应力)
表7为测点位移平均值与位移根方差结果.由表可知,数值模拟的测点位移平均值与试验值比较接近,测点1~测点6的位移根方差相差较大,测点7和测点8的根方差与试验值较为接近.分析试验现象,特征湍流可能引起部分膜片发生颤振的现象[10],测点振动幅度增大,FSI模拟无法再现试验中类似颤振的现象,有待在网格精细度、模型参数、算法等方面进一步改进.

表7 0o风向角的试验与数值模拟测点数据对比 mm
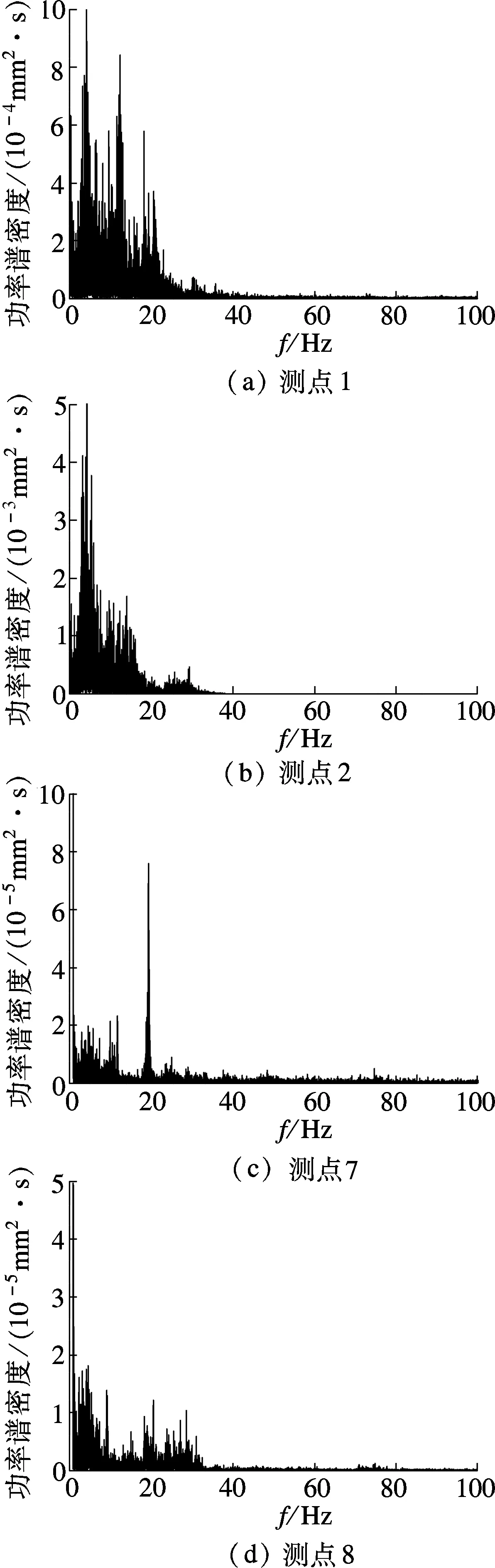
图19 位移功率谱(均匀流,v=10m/s,α=0o,低膜面应力)
选取结构前200阶的频率和振型,采用频域法计算结构脉动位移峰值分布,结果见图22.由图可知,最大值为0.58mm,位于试验测点2,3之间,对应的位移根方差为0.26mm.表7中,该位置附近的脉动位移根方差为0.29~0.84mm.与数值模拟结果相比,频域法能够考虑结构高阶模态对脉动位移的贡献,由频域法得到的位移根方差分布与试验结果更加接近.
5 结论
1) 在紊流风作用下,单片索膜做随机受迫振动,振动以背景响应为主,振动为宽带过程,脉动风会激起结构的某些振型.对于单片索膜结构,气弹模型试验、FSI数值模拟、频域法结果较为接近.膜面局部振动对风场分布影响较小.

图20 加速度功率谱(均匀流,v=10m/s,α=0o,低膜面应力)

图21 网格划分示意图
2) 单层索网玻璃幕墙在风荷载作用下振动为窄带过程,共振分量所占比重较大.不考虑玻璃面板,对单层索网进行频域法分析,由于忽略了玻璃的刚度,与索网幕墙数值模型相比,单层索网测点的平均位移、脉动位移都有不同程度的增大.工程中将玻璃幕墙简化为索网,通过频域法计算结构风振响应偏于保守.
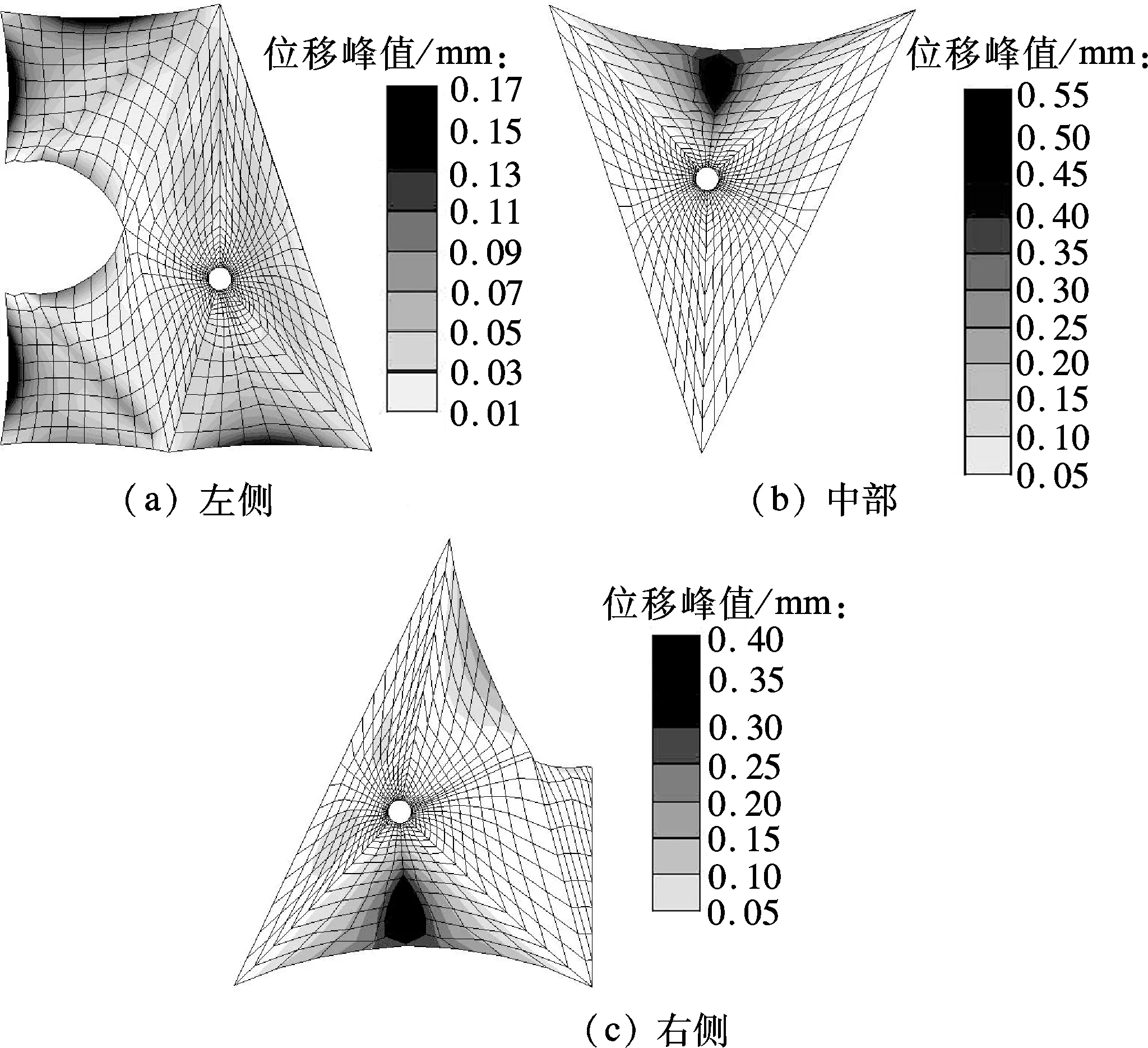
图22 脉动位移峰值分布
3) 均匀来流在膜结构屋盖表面形成特征湍流,使得某些膜片振动幅度较大,发生了类似颤振的现象.FSI数值模拟无法再现试验中类似的现象.基于随机振动理论的频域法能够考虑高阶模态对振动的贡献,脉动位移结果更接近试验值.
4) 对于张拉结构的风致振动响应研究,仍需在现场实测、风洞试验、数值模拟和理论方法等各方面开展长期、深入的研究.
)
[1] Vickery B J, Majowiecki M. Wind induced response of a cable supported stadium roof [J].JournalofWindEngineeringandIndustrialAerodynamics, 1992,42(1/2/3): 1447-1458.
[2] Nakamura O, Tamura Y, Miyashita K, et al. A case study of wind pressure and wind-induced vibration of a large span open-type roof [J].JournalofWindEngineeringandIndustrialAerodynamics,1994,52(1/2/3):237-248.
[3] Yasushi Uematsu, Theodore Stathopoulos, Eri Iizumi. Wind loads on free-standing canopy roofs. Part 1: local wind pressures [J].JournalofWindEngineeringandIndustrialAerodynamics, 2008,96(6/7): 1015-1028.
[4] Kinya Ando, Atush Ishi, Toshio Suzuki, et al. Design and construction of a double membrane air-supported structure [J].EngineeringStructures, 1999,21(8): 786-794.
[5] Michalski A, Kermel P D, Haug E, et al. Validation of the computational fluid—structure interaction simulation at real-scale tests of a flexible 29 m umbrella in natural wind flow [J].JournalofWindEngineeringandIndustrialAerodynamics, 2011,99(4): 400-413.
[6] 孙晓颖, 武岳, 沈世钊. 薄膜结构流固耦合效应的简化数值模拟方法[J]. 土木工程学报, 2010, 43(10): 30-35.
Sun Xiaoying, Wu Yue, Shen Shizhao. A combined numerical approach for wind-structure interaction of membrane structures[J].ChinaCivilEngineeringJournal, 2010,43(10): 30-35.(in Chinese)
[7] Bathe K J. Adina theory and modeling guide [EB/OL]. (2008-02-02)[2013-03-01]. http://www.adina.com.
[8] Masanao Nakayama, Yasuhito Sasaki, Keiji Masuda, et al. An efficient method for selection of vibration modes contributory to wind response on dome-like roofs [J].JournalofWindEngineeringandIndustrialAerodynamics, 1998,73(1): 31-43.
[9] 中国建筑科学研究院. JGJ 102—2003玻璃幕墙工程技术规范[S]. 北京:中国建筑工业出版社, 2003.
[10] Vitale A M, Letchford C M. Experimental study of wind effects on flat porous fabric roofs [C]//ProceedingsofWindEngineeringintothe21stCentury. Rotterdam, the Netherlands, 1999:1545-1555.
