一类具有次凸位势的二阶系统的周期解

王少敏，杨存基

（大理学院数学与计算机学院，云南大理 671003）

1 引言和主要结果

考虑二阶系统

（A）F（t，x）对于每个 x∈RN关于 t可测，对于a.e.t∈［0，T］关于 x 是连续可微的，存在 a∈C（R+，R+），b∈L1（0，T；R+）使得

对于 x∈RN和 a.e.t∈［0，T］成立。

其等价于如下范数

相应泛函

当 q（t）≡0，t∈［0，T］时，在假设（A）和一些适当的条件下，通过使用最小作用原理和临界点理论中的极大极小方法，人们已经获得了很多存在性结果〔2-12〕。

本文的主要结果如下：

定理1设F（t，x）＝F1（t，x）+F2（t，x）满足假设（A）以及F1（t，x），F2（t，x）满足以下条件：

（i）F1（t，·）是（λ，μ）－次凸的且存在δ∈［0，2），β、γ∈L1（0，T；R）

（ii）存在 f∈L2（0，T；R）且k∈L1（0，T；R）使得

2 定理的证明

我们知道存在一个常数c0>0，使得

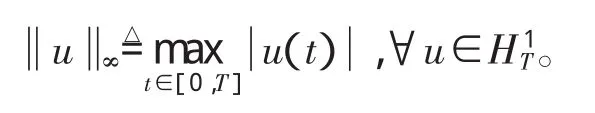
如果函数G：RN→R满足

G（λ（x+y））≤μ（G（x）+G（y）），∀x，y∈RN

称函数G为（λ，μ）－次凸的。

证明：由F1（t，·）的（λ，μ）－次凸性及S o b o l e v不等式，有

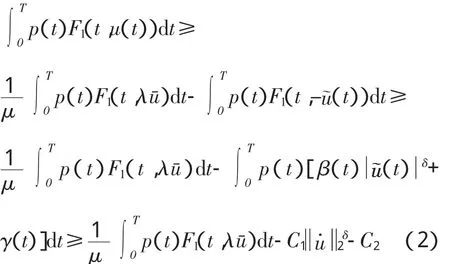
由（2）式，（3）式，有

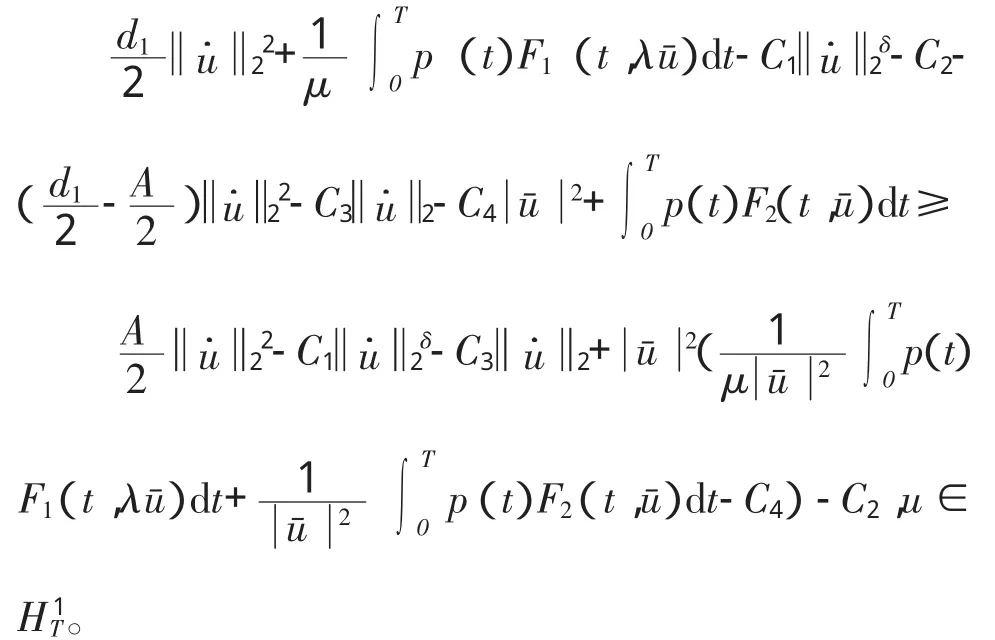
注：定理的条件是全新的；所以，文中所得结果是全新的。

〔1〕 Wu Xian，Chen Shaoxiong，Teng Kaimin.On variational methods for a class of damped vibration problems〔J〕.Nonlinear Anal.，2008，68（6）：1432-1441.

〔2〕Berger M，Schechter M.On the solvability of semi-linear gradient operator equations〔J〕.Adv.Math.，1977，25（2）：97-132.

〔3〕Mawhin J，Willem M.Critical Point Theory and Hamiltonian Systems〔M〕.Springer-Verlag：Berlin/New York，1989.

〔4〕Mawhin J.Semi-coercive monotone variational problems〔J〕.Acad.Roy.Belg.Bull.Cl.Sci.，1987，73（5）：118-130.

〔5〕Ma Jian，Tang Chunlei.Periodic solutions for some nonautonomous second order systems〔J〕.J.Math.Anal.Appl.，2002，275（2），482-492.

〔6〕Tang Chunlei.Eriodic solutions of non-autonomous second order systems with-quasisub-additive potential〔J〕.J.Math.Anal.Appl.，1995（189）：671-675.

〔7〕Tang Chunlei.Periodic solutions of non-autonomous second order systems〔J〕.J.Math.Anal.Appl.，1996（202）：465-469.

〔8〕Tang Chunlei.Periodic solutions for non-autonomous second order systems with sublinear nonlinearity〔J〕.Proc.Amer.Math.Soc.，1998（126）：3263-3270.

〔9〕Tang Chunlei，Wu Xingping.Periodic solutions for second order systems with not uniformly coercive potential〔J〕.J.Math.Anal.Appl.，2001（259）：386-397.

〔10〕Wu Xingping，Tang Chunlei.Periodic solutions of a class of non-autonomous second order systems〔J〕.J.Math.Anal.Appl.，1999（236）：227-235.

〔11〕王少敏，熊明，茶国智.一类非自治二阶系统的周期解〔J〕.大理学院学报，2012，11（4）：11-13.

〔12〕张绍康.一阶时滞微分方程的周期解〔J〕.云南师范大学学报：自然科学版，2010，30（4）：18-21.