基于点云的球面三维逆向建模

李胜男， 林 晓, ， 陈 言， 马利庄

( 1. 上海交通大学电子信息与电气工程学院，上海 200240；2. 洛阳师范学院信息技术学院，河南 洛阳 471000）

逆向建模指的是通过对工程中扫描得到的点云数据经过拟合计算，得到三维空间模型的一种方法。对球面点云的拟合[1]来说，尤其是对只有不完整球面的扫描数据点云来说，本算法在工程上有广泛的应用价值，不仅在零件检测、建筑物结构恢复等方面应用广泛，在气象学和考古学等领域也逐渐崭露头角，显示出其不可替代的作用。本算法利用激光扫描获得的点云来拟合球面和圆柱面，恢复被遮挡物的原貌；对于不全的图形，将其整体图形展示出来，为后续工作打下基础。

现阶段，球面和圆柱面等二次曲面的拟合主要是利用非线性最小二乘法[2-4]中的LM[5]算法进行迭代计算。然而，LM算法收敛次数会受到初始值设定的影响，从而影响计算速度，并有可能由于收敛次数过多而在漫长的计算之后失败，得到不准确的结果。2005年，Tahir Rabbani Shah[6]提供了一种通过对二次曲面的一般式全部九个参数直接拟合计算的方法，为二次曲面拟合开辟了一条新路。2008年Wenjuan Sun[7]提出对小角度的一段表面进行球面拟合的方法，2011年张之孔[8]提出加权二次曲面高程拟合方法及精度分析，这些都在一定程度上推动了球面拟合算法的发展。

本文提出的直接拟合方法(DF)结合以上算法，并提出改进，能够更快速准确的直接拟合出球面的几何参数。通过对球面添加不同程度高斯白噪声，算法给出了其对噪声的适应性分析。算法通过将点云切割分层整合计算和整体代入两种方法进行实现，并对比相应结果，分析得到相应结论。算法还对点云数量和点云分布位置等情况进行讨论，从而分析出影响算法结果的几个方面。

1 拟合算法

1.1 整体算法流程

本文提出的算法（以下简称DF算法）主要是通过3个过程得到最终的结果

首先，DF算法对收集到的点云数据进行预处理，初始化数据点，得到初始数据矩阵。

然后对初始数据矩阵进行运算，得到一个7×7的矩阵M，该矩阵是一个中间变量，用于计算拟合后表达式系数等相关参数。利用最小二乘法和拉格朗日乘数法算出球面一般式中的每项的系数，得到初步的参数。

最后计算出球面的最终参数和一些分析参数，将结果和LM算法以及自身对比分析。

1.2 拉格朗日乘数法

拉格朗日乘数法[9]是一种常见的求函数极值的方法，对于具有约束条件的函数来说，可以通过引入λ量进行求解，本文实现的球面拟合是以这个方法为基础的。

对于一个平面来说，我们可以设置平面法向量为n =(nx,ny,nz)，并且进行单位化，设|n| =1，将原点到这个平面的距离，我们设置为ρ，那么，对于任意一个点云中的点p =(px,py,pz)，我们可以计算它的到平面的正交距离，表示为n·p-ρ。为了优化点云中的点到这个平面的距离之和（最小二乘法得到拟合最佳结果），采用拉格朗日乘数法[9]：

图1 拉格朗日数乘法结构示意图

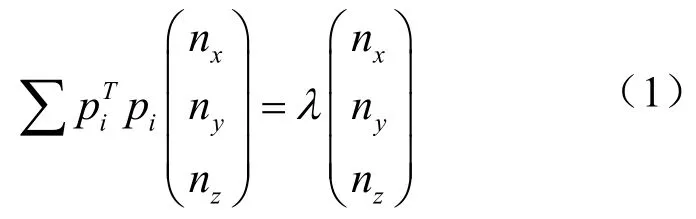
1.3 球面拟合计算

二次曲面都可以用一般形式表示出来：

对于球面来说，由于不存在交叉项，可以默认将f，g，h设置为零。由上面拉格朗日数乘法得到的结论，我们构建球面表达式：

对于球面来说，a,b,c应该是相等的。但是对于计算结果来说，他们在允许的条件下大致相等。对于我们的算法来说，我们只需要6个维度的未知量即可，所以我们追加了一个限制条件，系数的平方和等于1即

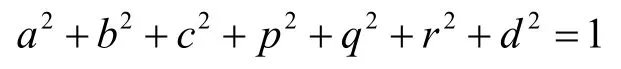
并且点云个数至少要大于7。

接下来我们就要构建上一部分计算的矩阵M，首先构建矩阵A：

对于任意一个点i，其中()是点云中的任意一个有效点的坐标。

M矩阵是一个7×7的矩阵，对于Tahir Rabbani Shah提出的算法进行了改进，提高了速度将近四倍。利用上一章阐述的拉格朗日乘数法，我们要得到的结果系数向量：

向量n是矩阵最小的特征值所对应的特征向量，通过求出向量n，从而得到一般式的系数，也就得到了利用最小二乘法计算的最短距离时对应的结果。利用这种方法，问题的主要部分得到解决。之后我们只需要对球的表达式进行配方等基本操作，就可以得到半径和圆心等几何参量。

1.4 计算结果的参数分析

对于球面来说，不仅仅需要计算球面的圆心和半径，我们还提供了4个参量对计算结果进行分析，他们分别是：

其中1λ是对半径的误差分析，R是求出来的计算值，R′是标准值。

E是点云中所有点距离球面的几何距离的平均值，是对球面误差的整体分析。

我们还保存了计算过程中使用的时间，来衡量计算的速度。

2 结果分析

2.1 与LM算法的对比

LM算法是非线性最小二乘法中被广泛应用的一种算法，它通过给出初始值和表达式形式，利用相应的迭代方法，进行收敛计算，从而得到球面的几何参数。下面我们就DF和LM算法进行对比分析。

2.1.1 算法时间

我们取经过预处理的模拟数据，并去掉背景空白的点作为初始有效点进行分析，分析的球实际位置为圆心在（0,0,0）点，半径为15。对LM算法和DF算法进行分别计算（下面如无说明，情况相同）。取不同的有效点数29081，7272，1818，451，分别计算它们所用的时间，得到下面的时间对比图：

图2 DF和LM算法时间对比

由图中可以看出，DF算法时间明显小于LM算法，而且在随着点数增加的同时，增长率明显小于LM算法，在速度上明显优于LM。而且DF算法只与有效点数有关，而LM算法还与迭代次数和迭代初始值相关。

2.1.2 算法精确度

在相同情况下，我们对衡量参数λ1，λ2和E都进行了分析计算，得到的结果如下：

图3 DF和LM算法半径误差值λ1对比

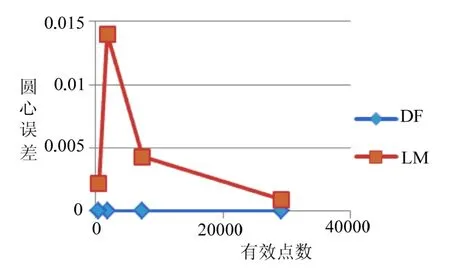
图4 DF和LM算法圆心误差值λ2对比

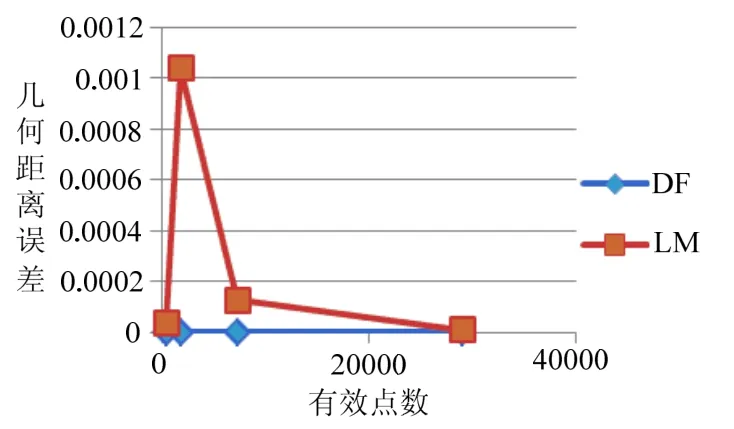
图5 DF和LM算法几何距离误差对比

对于3种误差的分析，我们无一例外的发现，DF算法的精确度明显高于LM算法，而且，LM的算法精确度不只是受到点数的影响，在1818点的时候还出现了跳变。而DF算法则不会有这种问题。

而且，DF算法对有效点数的要求不高，在这四种情况下，我们可以看到，误差基本不受有效点数的影响，而点数对于速度的影响是唯一的制约条件，我们可以在保持精确度不受影响的条件下，通过降低点数的条件下来提高速度，这是一个DF算法相对于LM算法的另一个优点。不过降低点数不能极端地影响点云中点的分布，否则会对结构造成一定程度，甚至是很大的影响，后面会进行分析。

2.1.3 受噪声影响程度

由于在实际工程中，扫描会带来一定程度的高斯白噪声，所以，在相同点数29081的条件下，我们分别对两个算法添加了高斯白噪声，等级依次为0, 0.1, 0.2 和 0.5，并分别进行了比较，得到图6所示。

从受噪声影响情况来看，DF更容易受噪声影响，当噪声超过0.11之后DF的精确度会增加的非常快，在超过0.5之后已经失去了可信度和可比较价值，所以，我们可以承认，DF算法对噪声的敏感性很高，我们在运行计算之前需要结合去噪声等算法来提高精度，因为在噪声较低的情况下，DF算法的可用性很高。

图6 DF和LM算法受噪声影响对比

而噪声影响对于球面函数拟合的影响是否重要，这要看工程上的具体要求。一般来说，采集到的点云都带有噪声，但是强度并不是很大，在误差允许的范围之内。影响拟合精度的原因很大程度上来说，是数据点只采集到球面的一部分而不是全部，或者由于遮挡等关系，造成点云数据的不全面，所以DF算法对于噪声的影响还是在可接受范围内的，而噪声在0.1左右的时候，DF算法并未受到明显的影响。

2.2 对点云进行分组计算对结果的影响

由于精度对数据点的个数并没有特别大的影响，所以，我们尝试通过先分组计算，最后整合各组数据来得到结果。但是，得到的结果并不理想，而且，对于数据量较少（10～100之间）的情况下，数据点的位置分布也对拟合的结果影响较大。

3 结 论

本文提出了一种球面拟合的方法实现基于点云的球面三维逆向建模，并在速度和精度上都取得了较为理想的结果。通过与LM算法的对比分析，得出了DF算法的优越性，和对噪声影响敏感这一个需要改善的问题的结论，还提出需要在之前结合去噪分析的建议来改善噪声对结果的影响。本文也对分组和在数据量较少的前提下的数据位置对结果影响进行了分析，为之后后续工作的研究提供了方向。

[1]Cavalier T M, Lehtihet E A, Del Castillo E, et al. An adaptive sphere-fitting method for sequential tolerance control [J]. International Journal of Production Research, 2002, 40(12): 2757-2767.

[2]Levenberg K. A method for the solution of certain non-linear problems in least squares [J]. Quarterly of Applied Mathematics, 1944, 2(2): 164-168.

[3]宋敏清,丁国清, 颜国正. 一种基于最小二乘估计的玻壳曲面拟合方法[J]. 计算机测量与控制, 2004,12(6): 569-571.

[4]杨恒亮, 屠大维, 赵其杰. 基于三坐标测量机的大口径球面拟合测量方法[J]. 工具技术, 2007, 41(12):78-81.

[5]Ananth R. The levenberg-marquardt algorithm [R]. 8th June, 2004.

[6]Rabbani T S. Automatic reconstruction of industrial installations using point clouds and images [D]. Delft University of Technology, 2006.

[7]Sun Wenjuan, Hill M, McBride J W. An investigation of the robustness of the nonlinear least-squares sphere fitting method to small segment angle surfaces [J].Precision Engineering, 2008, 32(1): 55-62

[8]张之孔. 加权二次曲面高程拟合方法及精度分析[J].测绘科学与工程, 2011, 31(2): 26-28.

[9]Vapnyarskii I B. Lagrange multipliers [M]. Hazewinkel,Michiel. Encyclopedia of Mathematics. Berlin:Springer. ISBN 978-1-55608-010-4.