同步性对“双缸多阀”电液振动台性能的影响
2013-03-20陈文颍宋琼舒杨
陈文颍,宋琼,舒杨
(中国工程物理研究院总体工程研究所,四川绵阳621900)
电液振动台以其出力大、体积小等优点,成为了离心机机载振动台的最优选择,用于开展缩比模型的地震模拟试验[1-2]。在离心场环境下,存在能量缩比以及时间缩比效应,地震波加速度信号的频率范围以及信号幅值将成倍提高,其缩比比例即为离心加速度g (g=9.8 m/s2)值。例如在50g 离心场环境下,频率上限为5 Hz的地震原型波经时间压缩后,频率上限将达到250 Hz。
电液振动台的频率特性受到伺服阀流量-频响特性的影响,伺服阀在小流量条件下频率响应高。为同时满足系统流量和频率范围的需求,需要使用多个伺服阀协同工作,以保证伺服阀工作在小流量条件下。为了避免额外的负载扭矩,离心场下的电液振动台采用对称设计,“双缸多阀”成为了离心机机载振动台的最优技术路线。
“双缸多阀”方案有液压缸轴对称分布与镜对称分布两种构型,且各有优缺点:镜对称构型的振动出力与台面振动中线重合,不会因双缸出力不均造成结构变形,对系统同步性的要求较低,但结构紧凑度不高,离心机吊篮空间利用率低;轴对称构型的振动出力与台面振动中线不重合,会因双缸出力的不平衡产生对滑动导轨的侧向压力,要求更高的系统同步性,但其紧凑性好,离心机吊篮空间利用率高。因此,在解决双缸出力不同步问题的前提下,轴对称构型在工程实现上更具优势。
采用“双缸多阀”方案的电液振动台,受到液压缸或伺服阀加工精度的限制,系统中两个伺服阀-液压缸部分的机电特性是不可能完全一致的,这使得双缸在出力时必然存在一定的差别。另外,两个伺服阀-液压缸部分若在获取驱动信号上存在时延,将直接导致双缸出力的时序不同步,进而对整个系统的同步性产生不利影响。以下针对轴对称构型“双缸多阀”的电液振动台,从双缸制造公差、驱动信号时延等多个方面来研究双缸同步性对系统性能的影响程度。
1 系统数学模型
伺服阀-液压缸部分是整个电液振动台系统的核心。伺服阀-液压缸部分的工作过程可以由液压系统连续性三方程,即伺服阀节流口流量方程(1)、液压缸工作腔连续性方程(2)以及液压缸力平衡方程(3)来进行描述[3]。
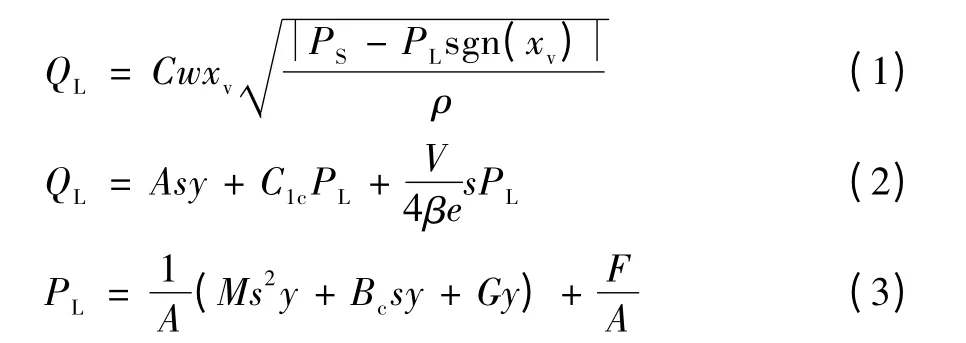
式(1)、(2)、(3)中:QL为负载流量;C为流量系数;w为伺服阀面积梯度;PS为供油压力;PL为负载压力;ρ为油液密度;xv为伺服阀阀芯开口;A为活塞面积;C1c为泄漏系数;βe为油液弹性模量;V为液压缸有效体积;y为试件位移;M为负载质量;Bc为负载阻尼系数;G为负载刚度;F为外力。
根据上述三方程,忽略伺服阀死区影响、液压缸活塞杆摩擦力,认为两个伺服阀-液压缸部分由同一信号驱动,且进行出力并联,这两个伺服阀-液压缸系统都将对方的出力视为液压缸力平衡方程中的外力F。由此构建出“双缸多阀”电液振动台的Matlab/Simulink 数学仿真模型如图1所示。
通过“振动波形相位差”与“振动波形幅值差”来衡量系统同步性对两缸振动出力同步性的影响程度。

式(4)中,“振动波形相位差”S 定义为两个振动波形的傅里叶频谱上所有对应频点相位差的绝对值均值(单位rad),θN为振动波形傅里叶频谱上第N个频点的能量相位。

式(5)中,“振动波形幅值差”D 定义为两个振动波形的傅里叶频谱上所有对应频点幅值差的绝对值之和与标准信号(可设定两个振动波形中的任意一个为标准信号)傅里叶频谱上所有频点幅值总和的比值,AN为振动波形傅里叶频谱上第N个频点的幅值。
还应得到双缸振动出力不均时所产生的对滑动导轨侧向压力的大小,以确定其是否会破坏系统结构。设定台面是一个正方形时,该侧向压力与双缸振动出力之差相等。
使用如图1所示的电液振动台的数学模型进行仿真,并针对出力达800 kN,工作于最高100g 离心场环境下,再现输出波形的有效频带范围为15~350 Hz的“双缸多阀”大型离心机机载电液振动台,设定其仿真参数如表1所示。

表1 电液振动台参数设定
2 加工精度及驱动信号时延对系统同步性的影响
液压缸的加工精度一般在0.01~0.1 mm之间,而伺服阀的加工精度要高得多,一般优于1 μm[4]。因此,在仿真分析过程中,可以忽略伺服阀的加工偏差。将液压缸的加工精度设定为0 (无偏差),0.01 mm,0.02 mm,0.05 mm,0.1 mm 这几个级别来进行仿真。使用经过100倍时间缩比的唐山大地震加速度振动波形作为驱动信号,得到液压缸的制造公差对两缸振动出力同步性的影响如表2所示。
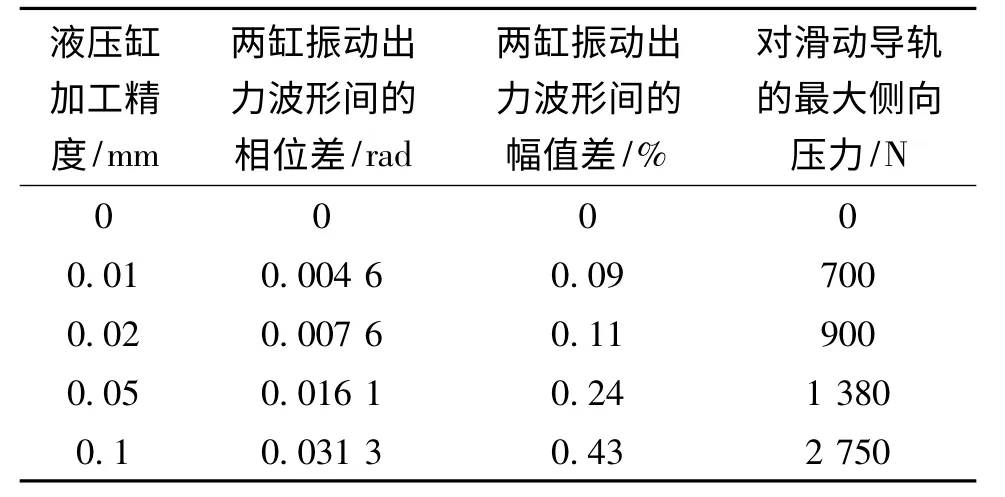
表2 液压缸制造公差对两缸振动出力同步性的影响
可以发现,在液压缸的加工精度范围内(0.01~0.1 mm),液压缸的加工偏差对两缸振动出力同步性的影响不大,所产生的对滑动导轨最大侧向压力也远小于滑动导轨的安全承力上限。
电液振动台控制模块的驱动信号刷新频率一般为1~10 kHz,若认为驱动信号时延比刷新时间间隔低一个数量级,可设定驱动信号时延为0 (无时延),0.01 ms,0.02 ms,0.05 ms,0.1 ms,0.2 ms,0.5 ms,1 ms 等级别来进行仿真。同样使用经过100倍时间缩比的唐山大地震加速度振动波形作为驱动信号,得到驱动信号时延对两缸振动出力同步性的影响如表3所示。
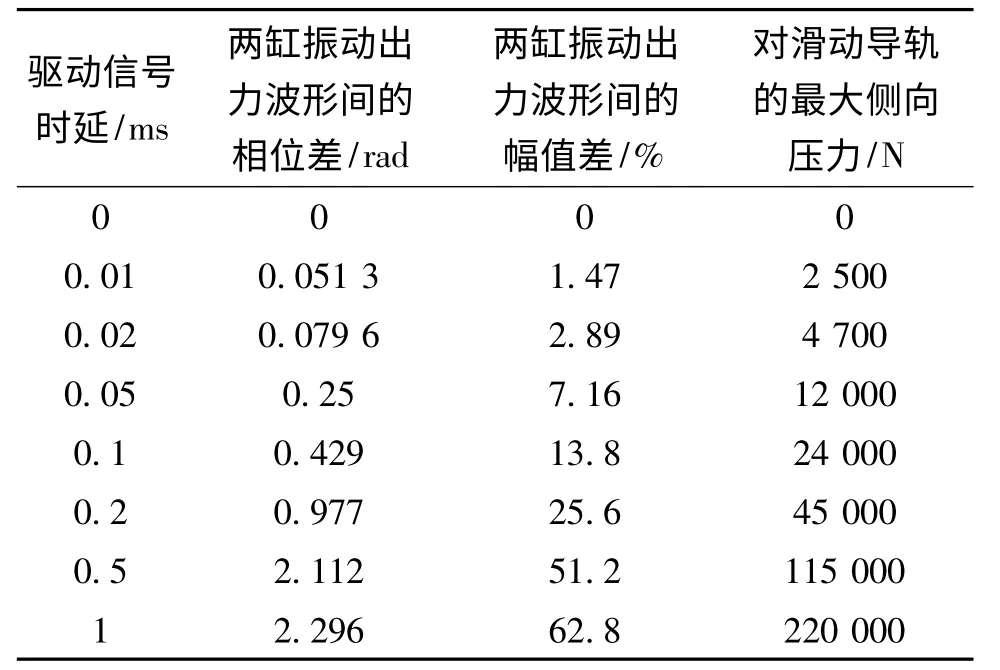
表3 驱动信号时延对两缸振动出力同步性的影响
对比表2可以发现,驱动信号时延对两缸振动出力同步性的影响要高于液压缸加工偏差。具体表现在以下3个方面:
(1)驱动信号时延引起的波形相位变化极其明显,这使得系统的非线性特征增加。因此,过大的驱动信号时延将使线性修正控制手段(如对驱动信号进行开环频域迭代修正)失效。
(2)驱动信号时延将造成两个伺服阀-液压缸部分极不平衡的振动力输出,这将使两缸之间产生严重的相互干扰。
(3)驱动信号时延还将引起一个很大的对滑动导轨侧向压力。在驱动信号时延较高时 (高于0.1 ms 这一量级),产生的压力将达到2~2×105N 甚至更高,这一量级压力虽然不会立刻破坏滑动导轨的承力结构,但会对整个系统的耐用性产生不良影响。
3 系统同步性对“双缸多阀”电液振动台地震波再现精度的影响
采用开环离线加速度频谱迭代修正方式对再现振动波形进行控制。并采用地震波失真度包括反应谱面积失真度、反应谱相位失真度,二者作为衡量波形再现效果的标准。
反应谱面积失真度定义为,再现波形与原始波形频谱面积之差同原始波形频谱总面积的比值。其反应了再现波形与原始波形之间的总能量失真情况,一般要求不高于5%。
反应谱相位失真度定义为,再现波形与原始波形的傅里叶频谱在各个频点上频谱幅值之差的绝对值之和同原始波形所有频点频谱幅值总和的比值。其反应了再现波形与原始波形之间频谱能量分布的失真情况。
使用经过100倍时间缩比的唐山大地震加速度振动波形作为驱动信号,设定液压缸加工精度分别为0(无偏差),0.01 mm,0.02 mm,0.05 mm,0.1 mm这几个级别来进行仿真。可得对应再现振动波形的失真度,如表4。
表4 液压缸加工精度对双缸系统的地震波失真度的影响
设定驱动信号时延分别为0 (无时延),0.01 ms,0.02 ms,0.05 ms,0.1 ms,0.2 ms,0.5 ms,1 ms 等级别完成仿真,可得对应再现振动波形的失真度,如表5。
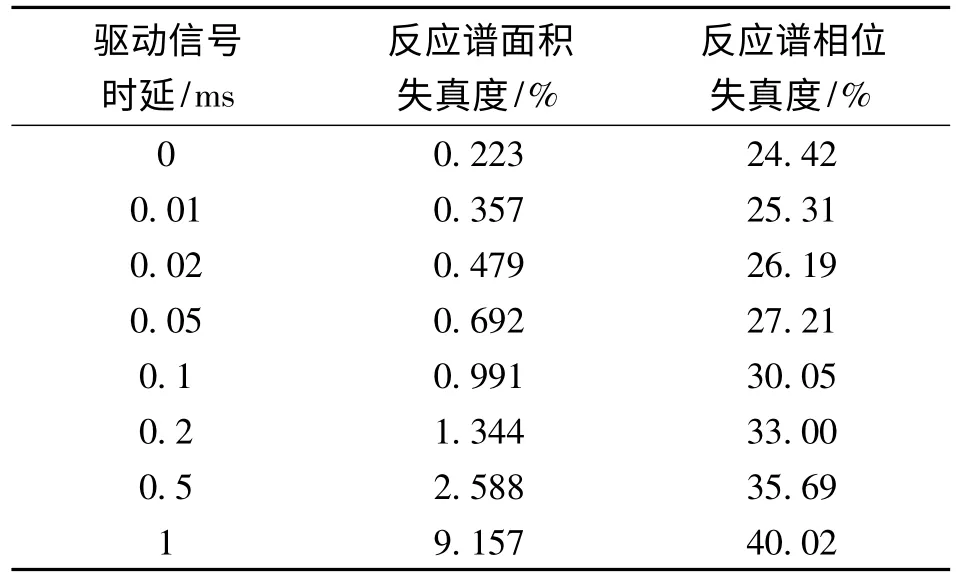
表5 驱动信号时延对双缸系统的地震波失真度的影响
4 结论
根据仿真结果可以得出以下结论:
(1)高于0.1 mm的液压缸加工精度与低于0.1 ms的驱动信号时延对再现振动波形的失真度影响有限。此时采用开环离线加速度频谱迭代修正方式可以获得较低的反应谱面积失真度(<1%)。
(2)当驱动信号时延高于0.1 ms时,采用开环离线加速度频谱控制方式能够获得的反应谱面积失真度与反应谱相位失真度都出现了显著的提升。随着时延的增加,控制手段逐渐失去了作用。
综上,能够认为液压缸加工精度对再现振动波形失真度的影响可以忽略。而驱动信号时延应尽可能低于0.1 ms以满足再现高频振动波形(如文中所设定的15~350 Hz 振动信号)的需求。
【1】VAN LAAK P A,ADALIER K,DOBRY R,et al.Design of RPI’s Large Servo Hydraulic Centrifuge shaker[C]//Proc.of Centrifuge,1998:105-110.
【2】冉光斌.土工离心机及振动台发展综述[J].环境技术,2007,6(3):25-29.
【3】黄浩华.地震模拟振动台的设计与应用技术[M].北京:地震出版社,2008.
【4】黎启柏.液压元件手册[M].北京:冶金工业出版社,1999.
【5】黄忠霖,周向明.控制系统MATLAB 计算及仿真实训[M].北京:国防工业出版社,2006.
猜你喜欢
杂志排行
机床与液压的其它文章
- Current Cloud Computing Security Concerns from Consumer Perspective
- Simulation of Hydraulic Servo System for High-Speed Injection Molding Machine by AMESim
- Research on Pneumatically Actuated 6-DOF Parallel Robot Based on SimMechanics
- Mechanical Amplifier for Giant Magnetostrictive Materials and Piezoelectric Materials
- 基于FANUC-0iTD的刀尖圆弧半径补偿应用研究
- 基于无线的数控机床联网
