三角域上双变量Chebyshev多项式及其与Bernstein基的转换

江 平， 洪为琴

（合肥工业大学数学学院，安徽 合肥 230009）

三角域上双变量Chebyshev多项式及其与Bernstein基的转换

江 平， 洪为琴

（合肥工业大学数学学院，安徽 合肥 230009）

为了更好的解决三角域上的Bézier曲面在CAGD中的最佳一致逼近问题，构造出了三角域上的双变量Chebyshev正交多项式，研究了与单变量Chebyshev多项式相类似的性质，并且给出了三角域上双变量Chebyshev基和Bernstein基的相互转换矩阵。通过实例比较双变量Chebyshev多项式与双变量Bernstein多项式以及双变量Jacobi多项式的最小零偏差的大小，阐述了双变量Chebyshev多项式的最小零偏差性。

三角域；Bernstein基；Chebyshev多项式

在CAGD中，有限域上的正交多项式对最小平方逼近问题起了十分重要的作用。在单变量情况下，Rababah[1-2]研究了 Chebyshev多项式和Jacobi多项式与 Bernstein多项式之间的转换公式，并利用构造的多项式演示了CAGD中Bézier曲面的最小平方逼近问题的求解过程；Faruoki[3]研究了Legendre多项式与Bernstein多项式之间的转换公式；利用约束Jacobi基作为工具，蔡华辉等[4]推导了 Jacobi基与 Bernstein基的转换公式。在双变量情况下，Faruoki等[5]构造出了三角域上的 Legendre多项式；Sawer[6]给出了三角域上Jacobi多项式的Bernstein基表示；Lewanowicz等[7]给出了三角域上Jacobi基与Bernstein基之间的转换公式；后来蔡华辉等[8]更简捷地构造出了三角域上的Jacobi多项式并给出了它与Bernstein基之间的转换公式。

曲线或曲面的基本表示形式都可以由Bernstein-Bézier基的线性组合来表示[9]，它具有计算稳定性等特点，但Bernstein多项式的非正交性使得它在最小平方逼近问题的求解过程十分的烦琐。因此研究二者之间的相互转换公式也是十分必要的。由于Bernstein多项式在CAGD中的特殊应用和研究背景，因此文章考虑了构造三角域上的双变量Chebyshev多项式。

受文献[5]和文献[8]的启发，在文章第一部分，结合单变量Chebyshev多项式的表达式构造出了三角域上的双变量Chebyshev多项式的表达式；然后在第二部分研究了它的性质，使得构造的多项式具有理论意义；进一步，在文章第三部分利用文献[1]中单变量情况下 Chebyshev基与Bernstein的基的转换公式，给出了三角域上的双变量情况下的基的转换公式，其中转换公式的系数是由单变量系数给出的，这使得构造的多项式便于实际的应用。

1 三角域上双变量Chebyshev多项式的构造

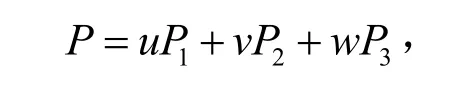
其中， u + v + w= 1。

三角域A上的Bernstein基函数[5]为：

三角域A上双变量Chebyshev多项式具有下面的分层排序：

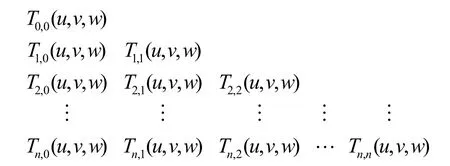
一共有(n+1)(n+2)/2个多项式，这些多项式就形成了中的三角域 A上的双变量 Chebyshev多项式在Chebyshev权下的一组正交基。

定义1 对于所有的n=0,1,2,…；r=0,1,2,…,n，三角域A上的双变量Chebyshev多项式为

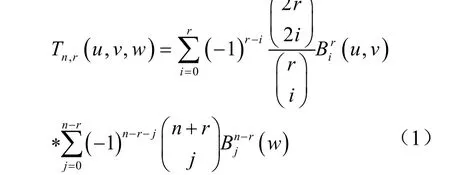
由于单变量Jacobi多项式[2]为

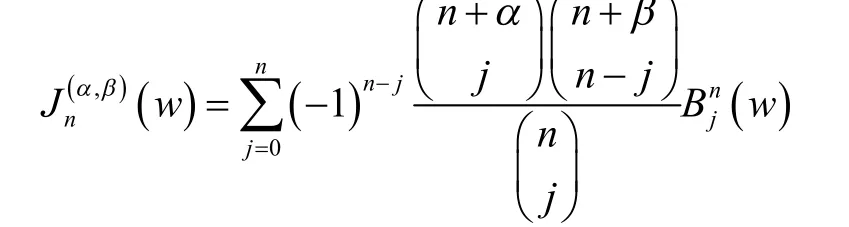
由文献[1]中单变量Chebyshev多项式知，双变量Chebyshev多项式可以改写为

其中，Tr(u)为单变量Chebyshev多项式。

在三角域上双变量Chebyshev多项式Tn,r(u, v, w)（其中,w=1-u- v）当n=0,1,2,3时的结果如下表：

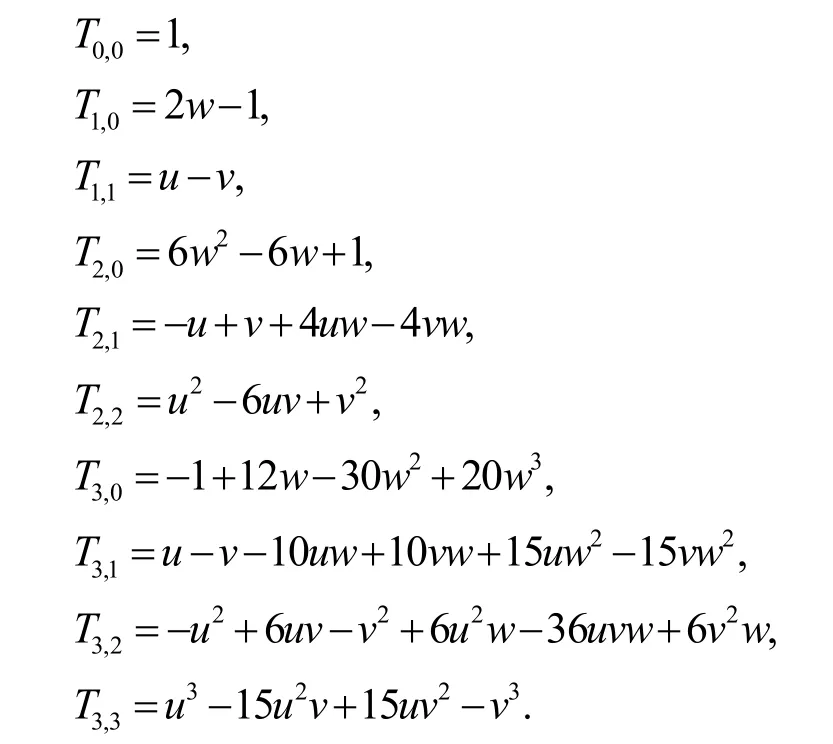
为了更直观的了解双变量Chebyshev多项式的特点和性质，下面画出当 n= 4时，的图像：

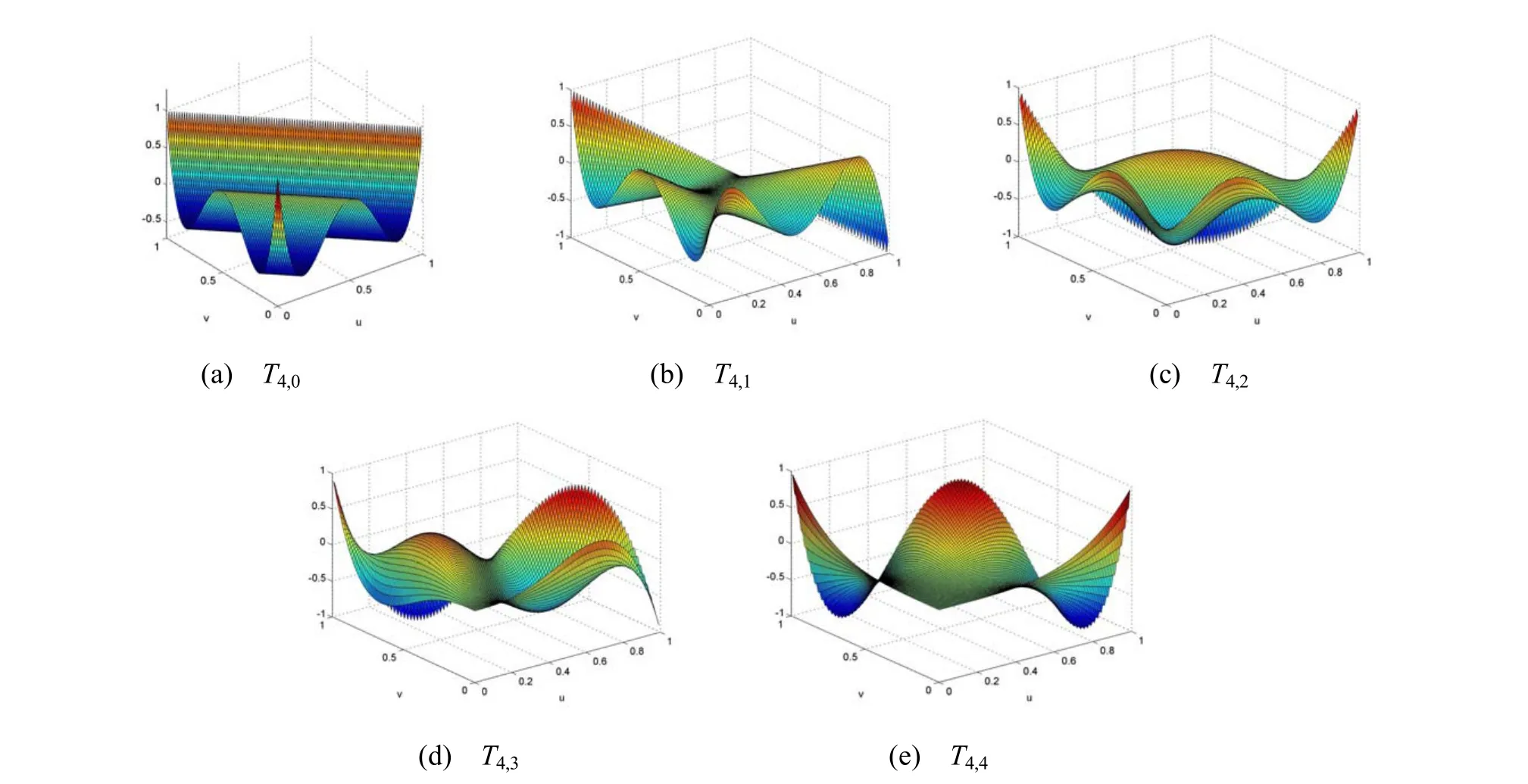
图1 当n=4(r=0, 1, 2, 3, 4)时，三角域A上的双变量Chebyshev多项式—Tn,r(u, v, w)

三角域上的双变量Jacobi多项式由下面的式子给出[8]：

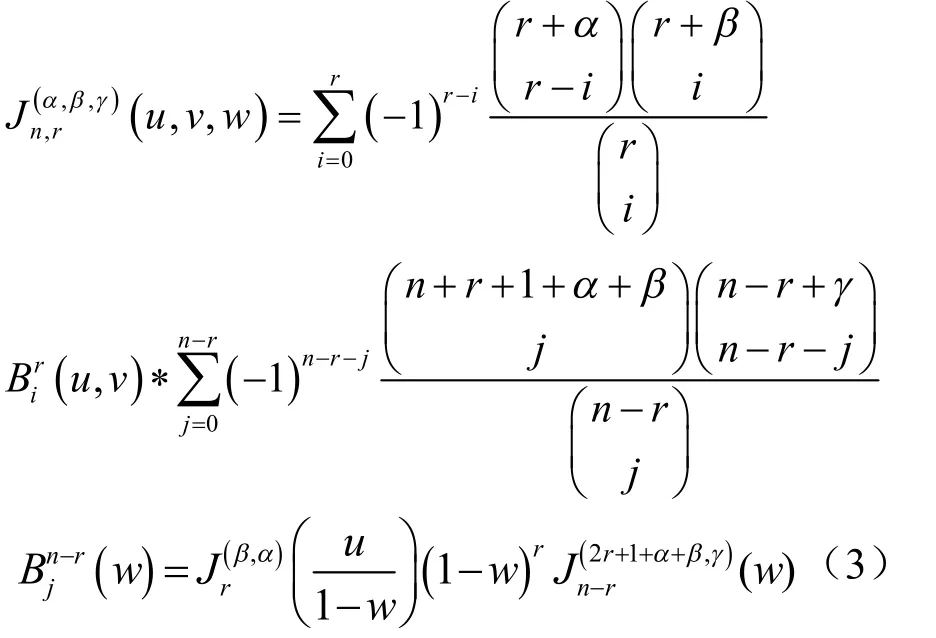
显然，Tn,r(u, v, w)在A的一条边界(w = 0)上恰好退化为权为时的单变量Chebyshev多项式 Tr( u)，且很容易可以看出定义中的 Tn,r(u, v, w)与文献[8]中当α = β =- 1 2,γ = 0时的双变量Jacobi多项式是一致的。

2 三式角性域质上双变量Chebyshev多项

下面研究三角域A上双变量Chebyshev多项式与单变量情况下相类似的性质：

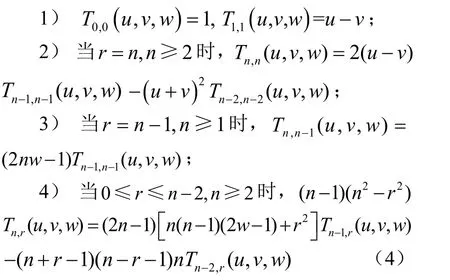
证明 当 r = n, n ≥ 2时，由式(2)和文献[1]有：

当 r = n - 1,n≥1时，

另外，当 r ≥ n -2,n ≥ 2时，由文献[10]知单变量Jacobi多项式当自变量x∈[-1,1]时的递推公式为

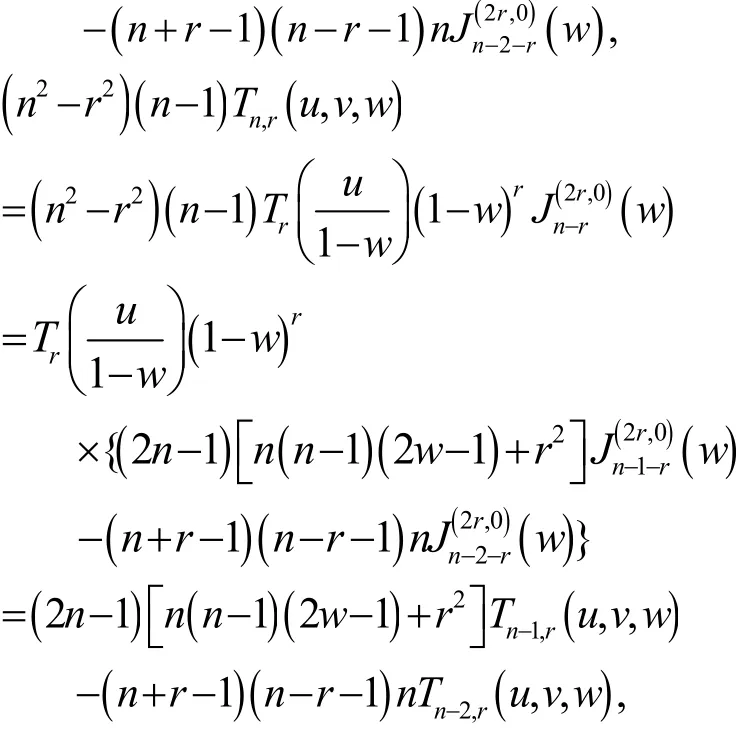
证毕

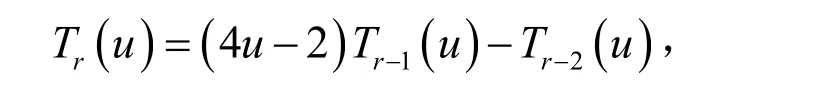
与单变量情况下的递推关系式是一致的。

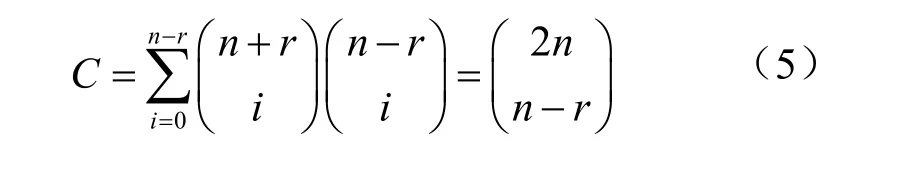
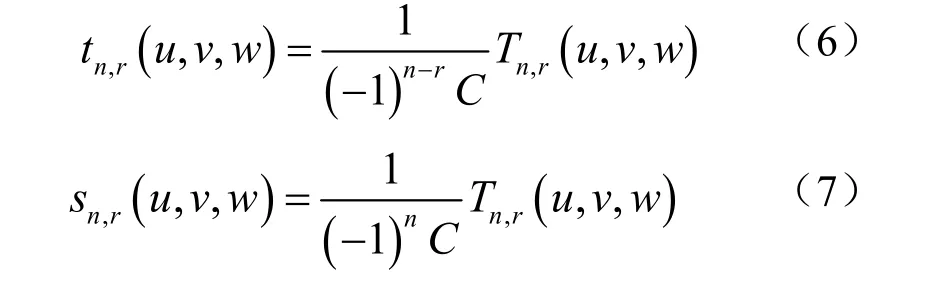
则在三角域A上有下面的结论成立：

双变量C he by sh ev多项式 T（u, v, w ）中n,r un（n≥ 1）和 vn（n≥ 1）的系数分别为（-1）n-rC和（-1 ）nC ；

证明：将 Tn,r（u, v, w）按u的次数从高到低排列，考虑u的最高次项，

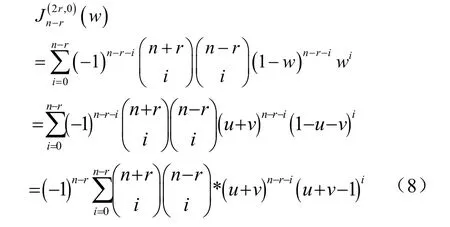
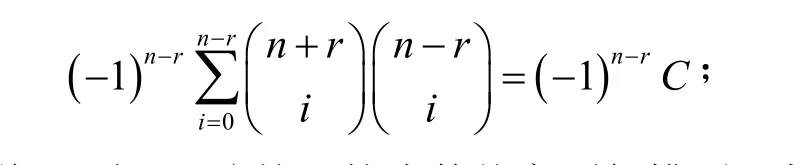
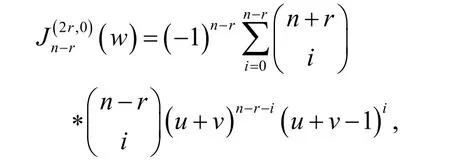
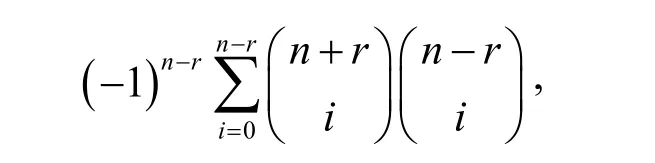
即Tn, r（u, v, w）关于v的最高次项系数为

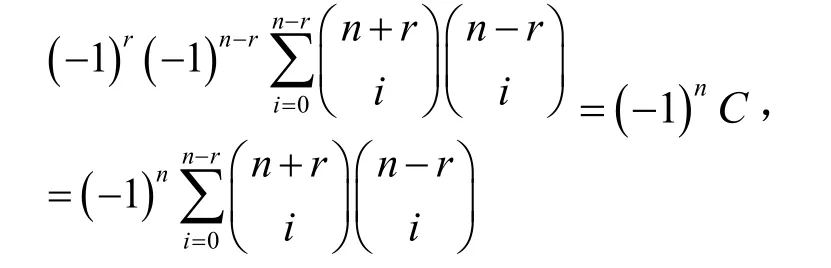
证毕

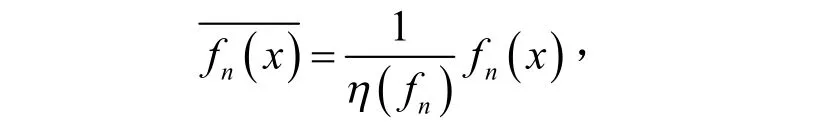
则首项系数为1的多项式的零偏差定义为

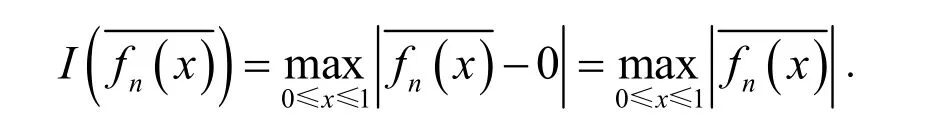
根据定理2以及零偏差的定义知

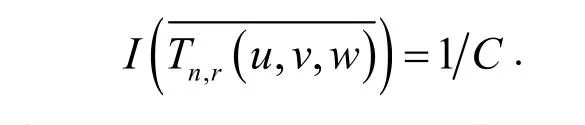
则由表 1可以给出当 n=4时，三角域上双变量Chebyshev多项式、Jacobi多项式和Bernstein多项式的零偏差的大小的比较。

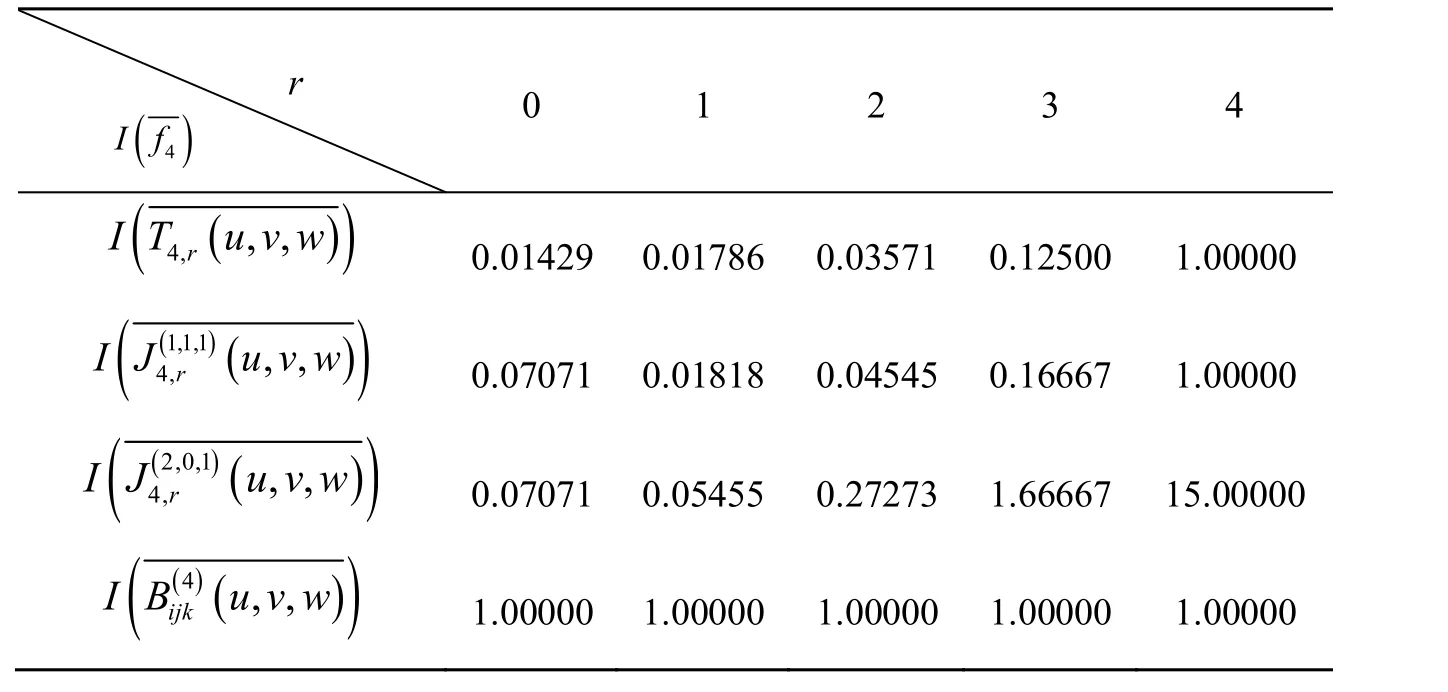
表1 当n=4时，三角域上双变量Chebyshev多项式、Jacobi多项式和Bernstein多项式的零偏差的大小的比较

通过上表不难看出，相较于首项系数为1的双变量Jacobi多项式和Bernstein多项式来说，双变量Chebyshev多项式在三角域上具有最小零偏差性，我们在今后的工作中可以进一步的研究最小零偏差性的证明过程。

定理3双变量多项式Chebyshev在三角域上带权正交，即

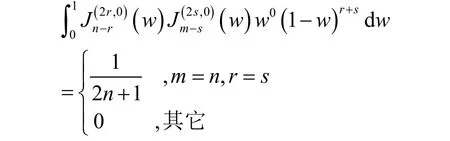
则有

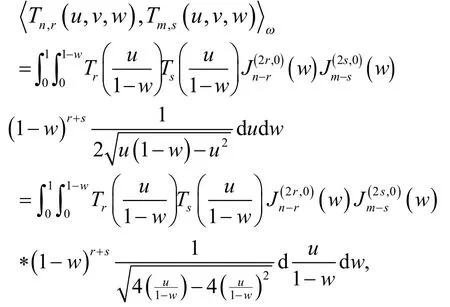
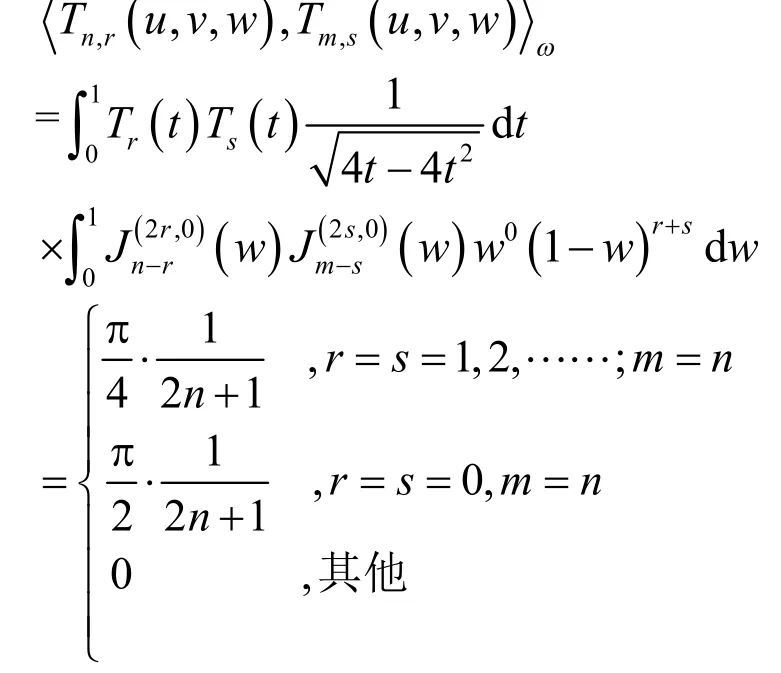
证毕

3 三角域上双变量Chebyshev基与Bernstein基的转换公式

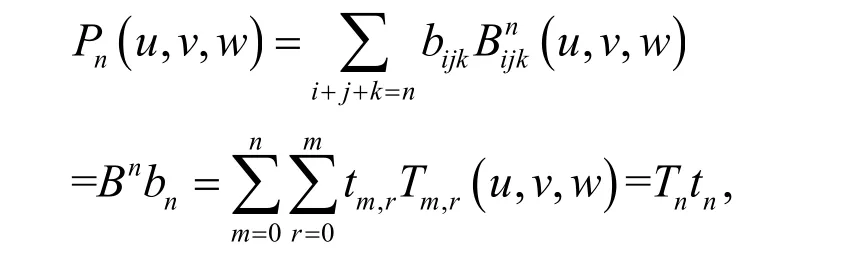
令

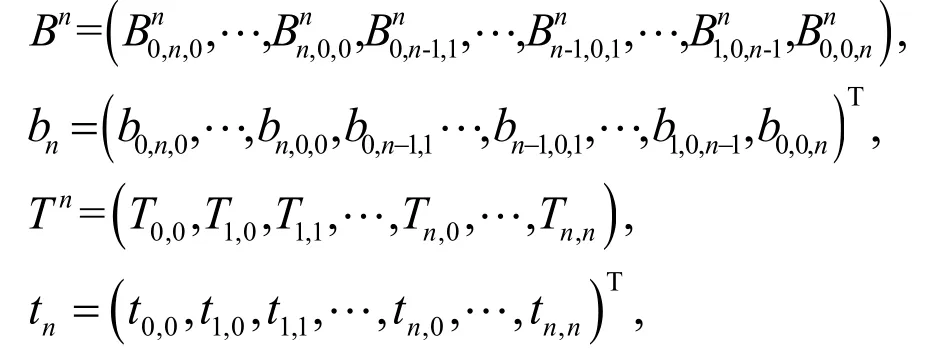
当12,n n都是大于0的整数时，其中

在文献[1]中有公式

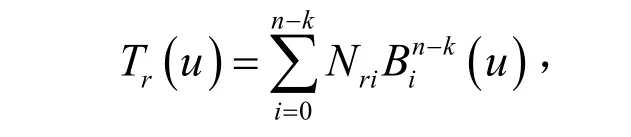
其中

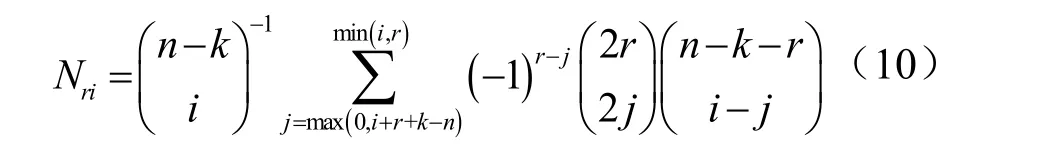
在文献[8]中有公式

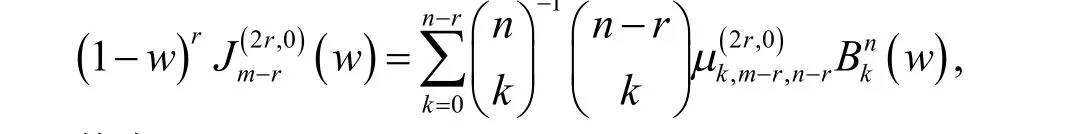
其中

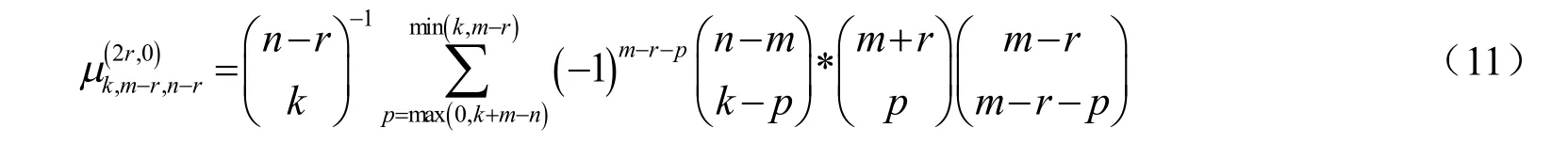
于是可以得到如下定理：

定理1

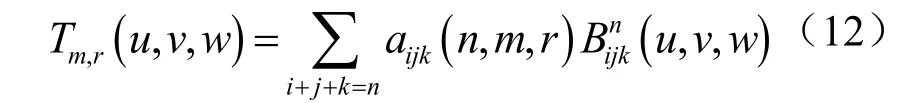
其中，

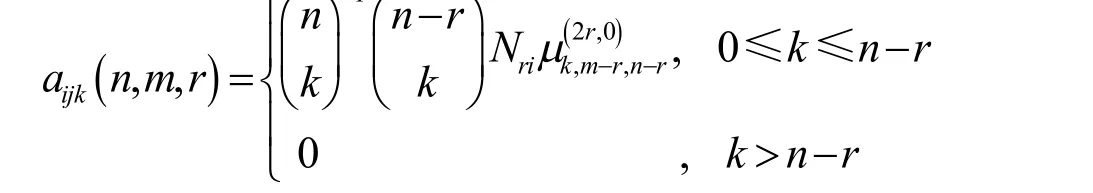
公式中的riN ,由式(10)和式(11)给出

证明：

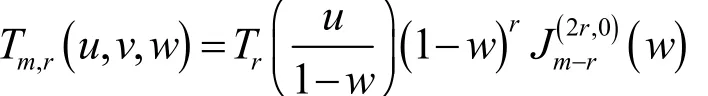
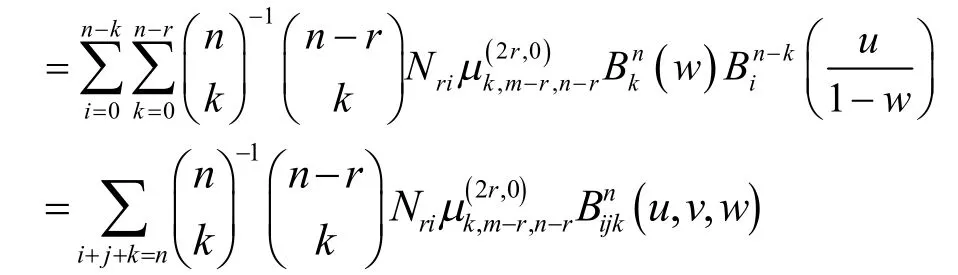
证毕

定理2

其中，

证毕

显然定理1 和定理2 的结论与文献[8]中当α = β = -1 2,γ = 0的结果一致。由文献[8]知道矩阵Μ中第行、第列元素就是，矩阵Μ 中第-1行，第列元素就是，即,其中

例1 当n=1时，设

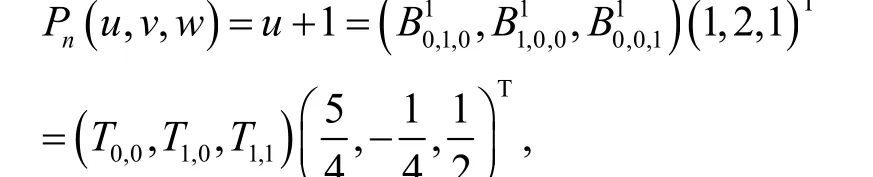
若

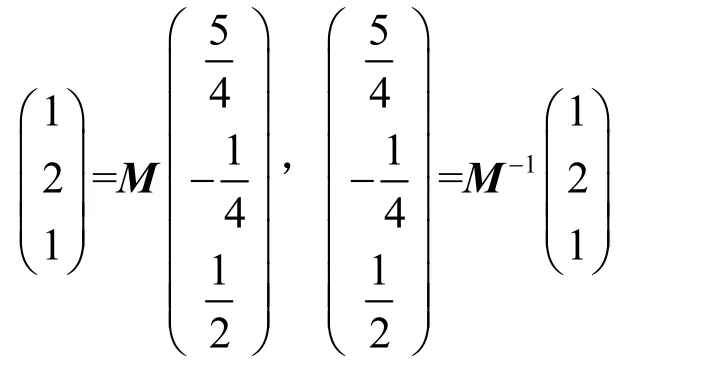
则由式(12)知

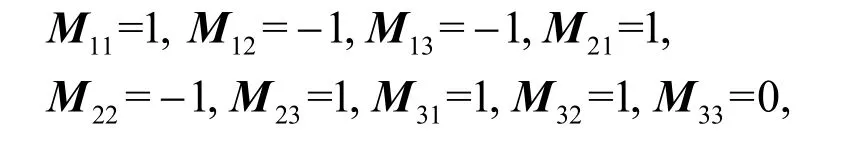
而由式(13)可以解出，

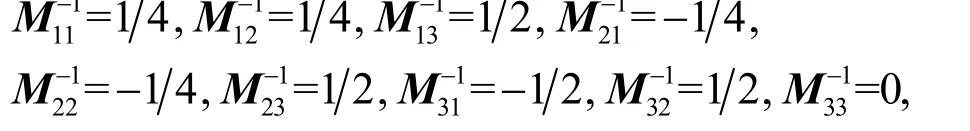
即有，

不难验算出下列等式成立，

4 结 语

文章给出了用重心坐标构造出的三角域上的双变量Chebyshev加权正交基，研究了它与单变量情况相类似的性质，并利用单变量的Chebyshev基与Bernstein基的转换公式推导出了双变量情况下二者的转换公式。并且通过给出具体的实例阐述了首项系数为 1的双变量Chebyshev多项式与首项系数为 1的双变量Jacobi多项式以及Bernstein多项式相比较具有最小零偏差性。在单变量 Chebyshev中，第一类Chebyshev多项式还有可以用三角函数来表示，文章并没有给出双变量Chebyshev多项式的三角函数表示，可以进一步研究双变量情况下的三角函数表示，那样在研究它的值域和递推关系式等等情况下会简便很多。另外，文章构造出的双变量Chebyshev多项式的最小零偏差性是通过数据实例来给出的，并没有给出具体的证明过程，而且文章提及的 Chebyshev多项式都是指第一类Chebyshev多项式。因此，今后可以进一步研究双变量Chebyshev多项式的最小零偏差性以及构造第二类双变量Chebyshev多项式的构造公式及其应用。

[1] Rababah A. Transformation of Chebyshev-Bernstein polynomials basis [J]. Computational Methods in Applied Mathematics, 2003, 3(2): 608-662.

[2] Rababah A. Jacobi-Bernstein basis transformation [J]. Computational Methods in Applied Mathematics, 2004, 4(2): 206-214.

[3] Farouki R T. Legendre-Bernstein basis transformations [J]. Journal of Computational and Applied Mathematics, 2000, 119(1): 145-160.

[4] 蔡华辉, 王国瑾. 基于约束 Jacobi 基的多项式反函数逼近及应用[J]. 计算机辅助设计与图形学学报, 2009, 21(2):137-142.

[5] Farouki R T, Goodman T N T, Sauer T. Construction of orthogonal bases for polynomials in Bernstein form on triangular and simplex domains [J]. Computer Aided Geometric Design, 2003, 20(2): 209-230.

[6] Sauer T. Jacobi polynomials in Bernstein form [J]. Journal of Computational and Applied Mathematics, 2007, 199(1): 149-158.

[7] Lewanowicz S. Woiny P. Connections between two-variable Bernstein and Jacobi polynomials on the triangle [J]. Journal of Computational and Applied Mathematics, 2006, 197(2): 520-523.

[8] 蔡华辉, 王国瑾. 三角域上双变量 Jacobi-Bernstein的基转换及其应用[J]. 计算机辅助设计与图形学学报, 2009, 21 (10):1394-1400.

[9] Farin G. Curves and surfaces for CAGD: a practical guide [M]. 5th ed. San Francisco: Morgan Kaufmann Publishers, 2002.

[10] 孙慧娟, 赵小香. 有关雅克比多项式一些性质的研究[J]. 四川理工学院学报(自然科学版), 2009, 22 (6):37-41.

Bivariate Chebyshev Polynomials and Transformation of Chebyshev-Bernstein Basis on Triangular Domains

Jiang Ping, Hong Weiqin
( School of Mathematics, Hefei University of Technology, Hefei Anhui 230009, China )

For solving least squares approximation problem of Bézier surface effectively and simply on triangular domains in CAGD, we present a polynomial representation, bivariate Chebyshev polynomials, adapted to a triangular domain, with properties similar to the univariate Chebyshev form．We convert and compare this representation to the Bernstein-Bézier and Jacobi representations．We also give some examples to illustrate that the deviation of the bivariate Chebyshev polynomials compared with zero is the least than of the bivariate Bernstein polynomials and bivariate Jacobi polynomials.

triangular domains; Bernstein basis; Chebyshev polynomial

TP 391

A

2095-302X (2013)06-0022-08

2013-02-25；定稿日期：2013-03-25

江 平（1972-），女，安徽枞阳人，副教授，博士，主要研究方向为计算机辅助几何设计。E-mail：jiangping_72@sina.com

洪为琴（1987-），女，安徽宿松人，硕士研究生，主要研究方向为计算机辅助几何设计。E-mail：494786700@qq.com