南京地层地铁隧道施工的Peck公式修正
2013-03-18郭延华吴龙海
郭延华,吴龙海
(河北工程大学土木工程学院,河北 邯郸,056038)
城市地铁隧道开挖容易造成开挖区域土体变形及沉降,导致周边建(构)筑物的变形和破坏,因此地表沉降的预测十分重要。1969年Peck提出估算隧道开外地表沉降的实用方法,总结得出地表沉降预测公式—Peck公式[1-2],并在之后的地铁隧道施工中广泛应用。由于不同地区地质条件的差异性,由Peck公式预测的沉降值与实测值不符,误差较大,需对其进行修正[3-4]。本文基于南京地铁2号线大量实测数据及地质条件,采用线性回归及线性拟合方法,对Peck公式进行修正,以获得良好的预测结果。
1 Peck经验公式的解析
1.1 Peck经验公式理论
在盾构掘进过程中产生地层损失,不考虑土体排水固结与蠕变的情况下,地层移动是一个随机过程,在盾构掘进过程中地表形成横向沉降槽为近似正态分布曲线,其预测地表沉降分布公
式为:
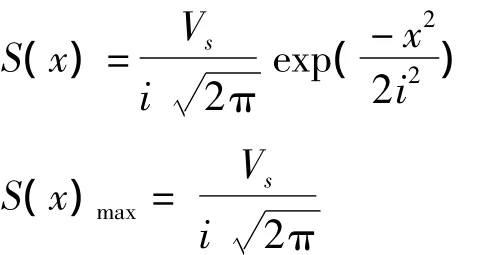
式中:S(x)-距离隧道中心轴线为x处地表沉降值;Vs-隧道单位长度地层损失;S(x)max-隧道中心线处地表最大沉降值;i-地表沉降槽宽度系数。
1.2 Peck经验公式参数计算
1.2.1 沉降槽宽度系数
New和O’Reilly提出单一土层中隧道掘进引起的地表沉降与施工方法、隧道直径无关,且沉降槽宽度i和隧道轴线埋深Z0之间存在简单线性关系

式中:K-沉降槽宽度系数;Z0-隧道轴线埋深。1.2.2 地层土体损失率
经验预测法预测地层土体损失率一般采用反分析法,通过地层沉降实测数据反分析得到i值,再反分析求出地层土体损失率η:

式中:R-盾构外径。
2 Peck经验公式线性回归
分析实测资料,可知实测地表沉降数据不是一条光滑曲线,但由于实测沉降值与测点距隧道轴线距离有一一对应关系,因此可通过一元线性回归分析,将实测数据拟合成一条曲线。
Peck教授提出的Peck公式是一个非线性函数,其函数表达式:
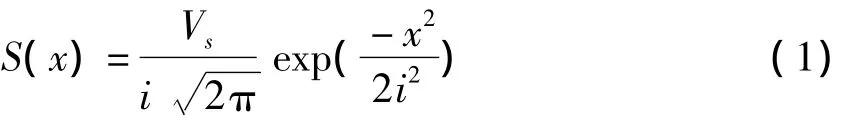
对Peck公式进行线性回归分析[5],需对其进行基本变换,由数学知识对式(1)两边同时取对数可得:
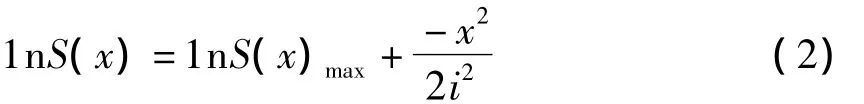
类比一元线性回归模型,lnS(x)与lnS(x)max之间存在线性相关关系:
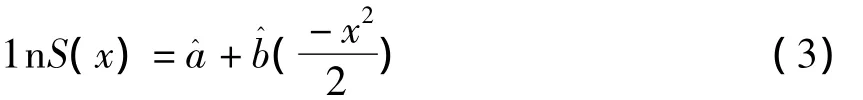
以(2)式中lnS(x)、-x2/2为回归变量进行线性回归运算,并利用最小二乘法确定回归转换后的线性函数,此时â、可作为一元线性模型中最小二乘估计值。
回归过程如下:

一元线性模型中最小二乘法估计值:

式中:xi-第i个样本点距隧道轴线距离的代表值;n-样本点个数。
由上述回归可得:

3 算例
现以玄武门~新模范马路区间A-A断面为例,运用上述方法对实测数据进行转换(表1)。
计算得到Sxx=8 404.928 57、Syy=3.279 9、Sxy=162.045 7,a=2.263 09、b=0.019 28,则回归后线性函数检验线性函数的相关性,得相关性高度显著。将回归函数与实测数据进行对比(图1)。
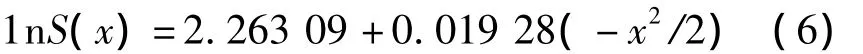

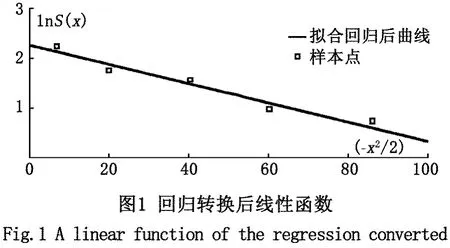
表1实测地表沉降数据回归分析Tab.1 Regression analysis of surface subsidence measured data
由图1可知,回归后的线性函数与实测数据拟合较好,能够很好的反映转换后实测数据之间关系。

由图2可以看出,拟合曲线与实测数据曲线吻合较好,说明运用一元线性回归方法能有效拟合地铁隧道开挖引起地表沉降的监测数据,同时从图中知原始Peck公式预测曲线与实测数据曲线有较大误差,故需对其进行修正以满足南京地区同地质条件下地铁隧道施工的预测需求[6-8]。
4 Peck经验公式的修正
4.1 Peck公式修正
综合考虑影响地铁施工隧道开挖引起地表沉降的各方面因素,对Peck公式中沉降槽宽度及地表最大沉降进行修正;修正后Peck公式如下:

式中:α-地表最大沉降修正系数;β-沉降槽宽度修正系数;S(x)max-原始Peck公式预测最大地表沉降;i-原始Peck公式预测沉降槽宽度;α、β-考虑各方面影响因素叠加后参数。
对式(6)线性转换

以A-A断面为例,其回归线性函数为
1nS(x)=2.263 09+0.019 28(-x2/2)

计算得a=0.506、β=0.918。
将计算得出的α、β修正参数代入Peck公式中,绘制出修正后预测曲线与实测拟合后曲线(图3)。

由图3可以看出,实测数据拟合后曲线与修正后预测曲线吻合较好,说明修正参数α、β只要取值合理,能够较好的修正原始Peck公式预测的结果。
根据上述修正方法,在南京地铁玄武门~新模范马路区间隧道的实际工程中,选取不同断面的实测数据,得到不同的修正值α、β,现对5个区域隧道的37组数据进行分析计算,得各区域修正系数分布(表2)。
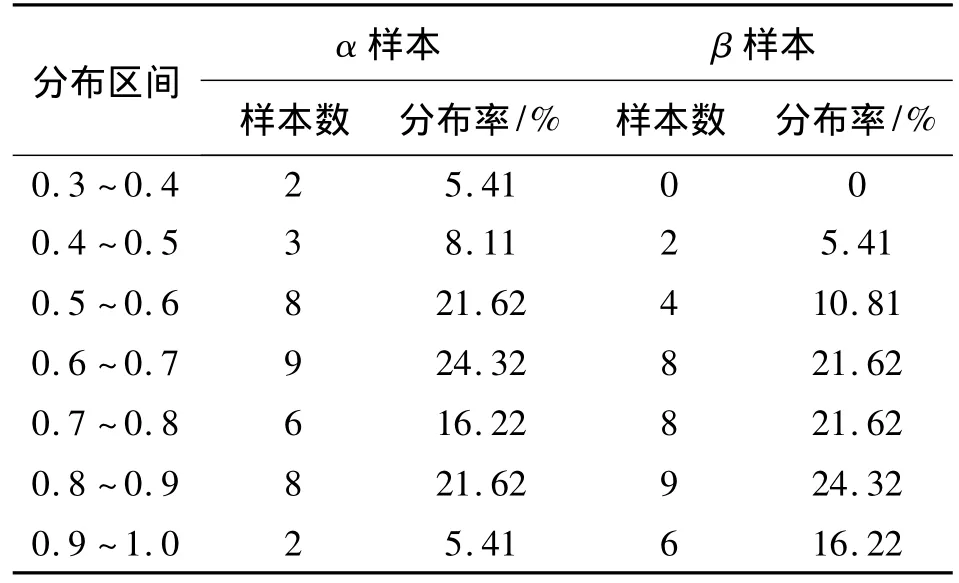
表2修正系数分析表Tab.2 Correction factor analysis table
从表2可知:地表最大沉降修正系数α介于0.5 ~0.9 时,分布率占到 81.07%,沉降槽宽度修正β介于0.6~1时,分布率占到83.78%;运用反分析法计算并统计出沉降槽宽度系数K介于0.35~0.75时,分布律占到98%,土体损失率η介于0.4%~0.85%时,分布率占到95%。综合可知:α介于0.5 ~0.9、β介于 0.6 ~1,K介于 0.35 ~0.75、η介于0.4%~0.85%时可较好的修正由Peck公式预测的地表沉降最大值与沉降槽宽度。
4.2 修正参数α、β的验证
选取α、β两个修正参数上下限的组合进行检验;上限:α为0.9、β为1;下限:α为0.5、β为0.6,则其它系数组合所得修正曲线均介于这两种情况之间,绘制出上下限Peck公式曲线与原始Peck公式曲线,同时从37组实测数据任选一组数据标定于图中进行对比(图4)。
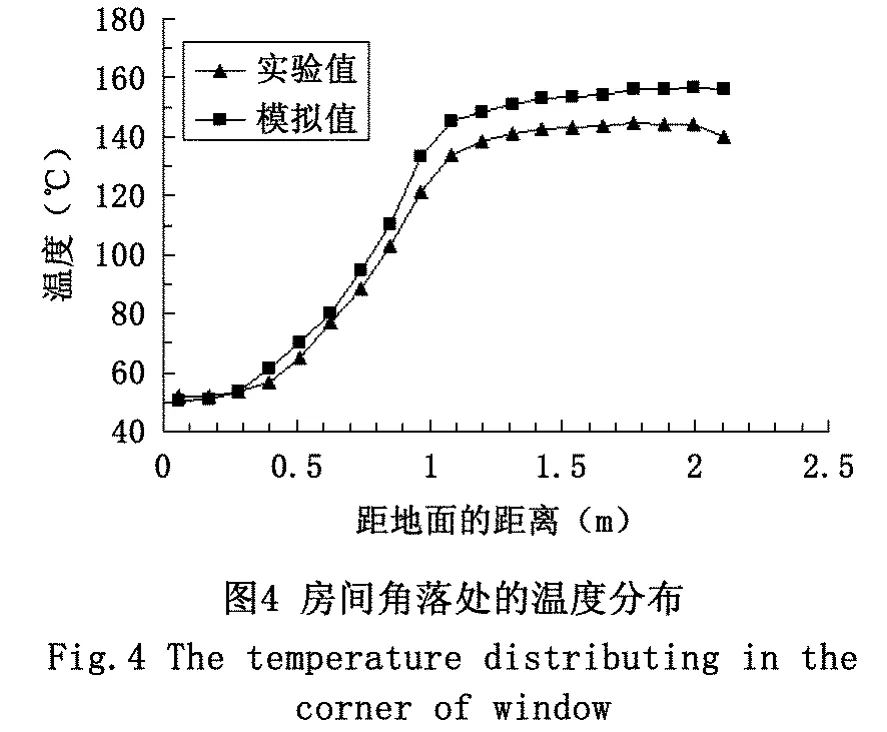
从图3中知,大部分观测数据落于上限与下限曲线之间,可推论:采用这种方法修正后的曲线能更好的预测实际地表沉降[9-11]。
5 结论
本文利用南京地铁隧道开挖监测监测得到的大量数据,对Peck公式进行参数修正。理论与实践结合表明:地表最大沉降修正值α介于0.5~0.9,沉降槽宽度β介于0.6~1,此时沉降槽宽度系数K介于0.35~0.75,土体损失率η介于 0.4%~0.85%,得到修正后Peck曲线与地表实测沉降数据更吻合。获得的修正参数仅针对南京地铁玄武门~新模范马路区间隧道,具有一定的局限性,对于其它地区地铁工程,可类比此法,以期达到预期效果。
[1]韩煊,李宁,STANDING J R.Peck公式在我国隧道施工地面变形预测中的适用性分析[J].岩土力学学报,2007,28(1):23 -28.
[2]王霆,刘维宁,张成满,等.地铁车站浅埋暗挖发施工引起地表沉降规律研究[J].岩石力学与工程学报,2007,26(9):855 -861.
[3]冯晓光,任建喜,王金华.西安黄土地层盾构施工的Peck公式修正[J].西安科技大学学报,2012,32(3):343-347.
[4]潘海泽,蒋冰玉,黄 涛.Peck公式在天津隧道盾构施工地面沉降预测中的适用性分析[J].测绘科学,2010,35(3):53 -55.
[5]应楚强,何春雄.数理统计[M].广州:华南理工大学出版社,2008.
[6]侯学渊,廖少明.盾构隧道沉降预估[J].地下工程与隧道,1993,(4):24 -32.
[7]张义同,高 健,乔金丽,等.隧道盾构掘进力学[M].天津:天津大学出版社,2010:75-142.
[8]罗章波.南京地铁一号线南京站车站隧道设计[C]//中国铁道学会.中国交通土建工程学术论文集.成都:西南交通大学出版社,2006.
[9]牟兆刚,王化耀,付学术.引水隧道井检孔水文地质特征及井筒涌水量预算[J].中国煤炭地质,2012,24(5):77-80.
[10]李建平.某铁路隧道隧址区水文地质条件分析与洞身涌水量预算[J].中国煤炭地质,2010,22(6):43-46.
[11]胡子建,周勇,朱建群,等.隧道开挖过程中软弱围岩的爆破技术研究[J].河北工程大学学报:自然科学版,2012,29(3):73 -76.
