差异维度传感器数据融合新方法
2013-03-18宋文彬
宋文彬
(中国西南电子技术研究所, 成都610036)
1 引 言
数据链技术的迅猛发展使得不同平台异类传感器协同探测、协同防御和协同攻击成为可能。用于目标跟踪的传感器有能获取完整目标三维位置信息的雷达、仅能探测目标二维方位信息的无源传感器(如红外传感器、ESM)、仅能测得目标一维距离信息的激光传感器等。在实际应用中,为了及时、准确、全面地获得战场信息,提高目标跟踪精度,需要将多种差异维度的传感器进行配合使用。当雷达与另一不足维量测传感器处在同一个平台时,一般可直接将角度或距离信息单列出来进行单维的加权融合处理;但当两者不处在同一平台时,量测误差在坐标变换的时候分量之间会发生耦合现象,造成无法直接进行距离或量测角度单维融合。针对后一种情形,如果第二种传感器是无源二维测向传感器,一种做法是通过目标或无源传感器搭载平台做机动实现三维跟踪滤波后,再将其与雷达量测进行融合[1-2]。朱志宇对异地配置下的雷达和红外传感器进行了数据融合,给出了融合后的目标方位,但并未确切给出坐标原点和距离参数,因而无法对目标进行定位[3]。王毅讨论了同样的问题,他是直接将雷达量测的距离信息与相对精确的红外量测的角度信息进行联立求解,而完全忽视了雷达量测的角度信息[4]。雷达与异地一维传感器量测的融合尚没有找到相关文献。本文的操作方法是首先将雷达探测数据转换到另一传感器的量测坐标系,得到相对应的距离和方位,然后将它们与另一传感器的量测直接进行融合。朱志宇等曾分析过将雷达探测数据转换至以红外传感器平台为坐标原点的东北天坐标系中[5],这种转换仅属于坐标平移与旋转的范畴,仍然不能与红外传感器量测直接进行融合,因此他们所作出的结果对目标定位精度的改善程度非常小。本文不同的地方是构造了一种近似等效的方法将直角坐标系下的量测协方差成功地转到了异地球坐标系下,然后以此为基础进行凸组合融合处理。
2 差异维度传感器数据融合方法
数据链实时通信使得异域传感器共同量测目标成为可能。举个例子,存在这样一种情形,前方的侦察机因隐身需要已关闭雷达,利用搭载的红外设备发现敌机,后方预警机利用雷达也发现了同一敌机,那么怎么才能将侦察机精确的目标方位信息和预警机精度较差的目标位置信息进行有效融合呢?再举一例,主机利用SAR 雷达发现了一座桥梁,友机在桥梁的另一侧对其进行了激光测距,SAR 雷达低精度的静止目标位置信息如何与激光高精度的测距信息实现融合呢? 本文的方法主要解决不同平台传感器对共同目标的三维量测与缺维量测如何进行融合的问题。
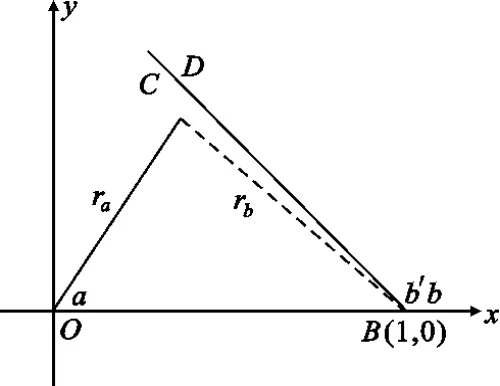
图1 雷达与无源传感器量测示意图Fig.1 Illustration of measurements obtained from radar and passive sensors
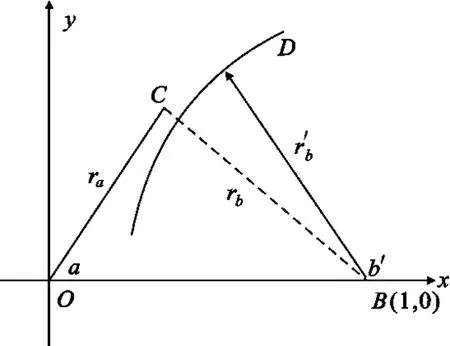
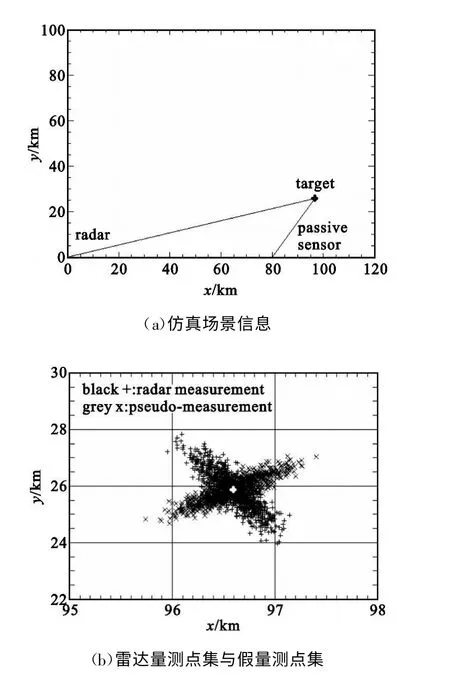
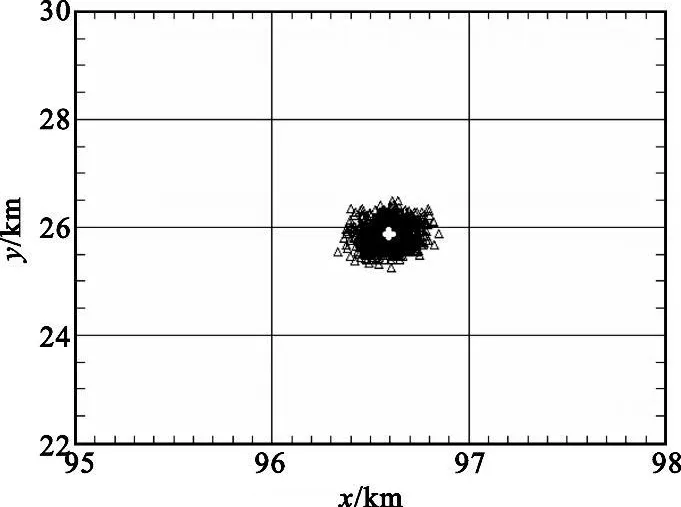
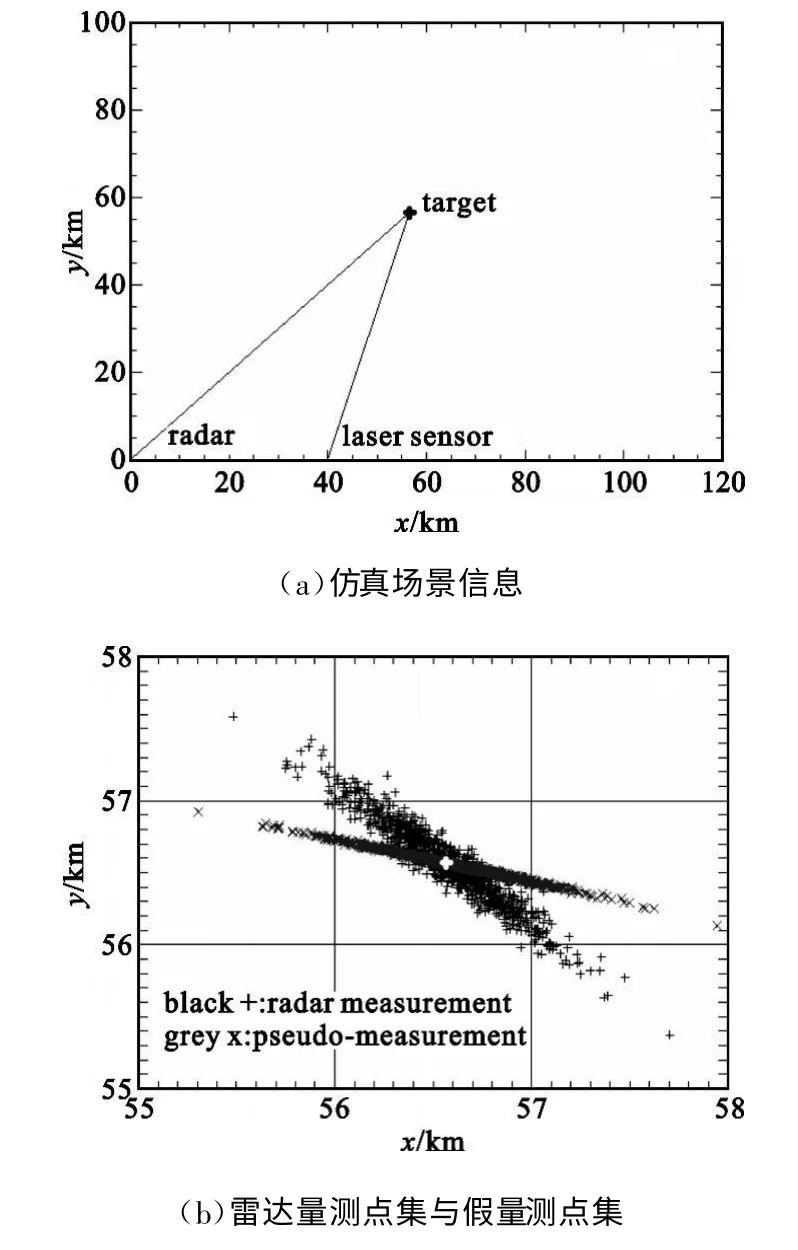
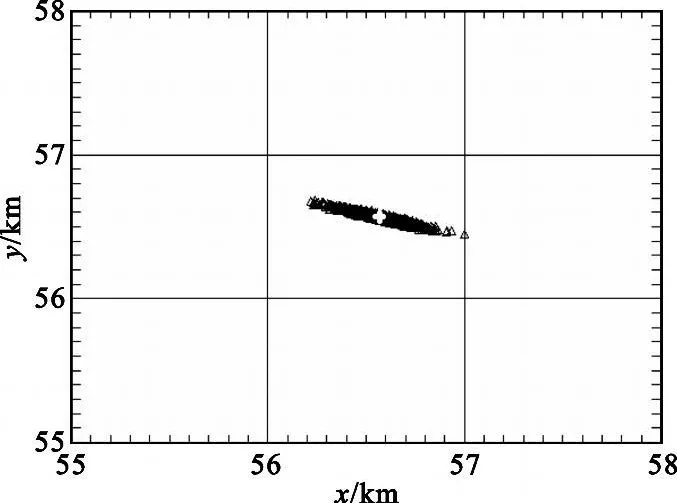
为说明方法及公式推导的简便,本文讨论场景如下:(1)二维场景;(2)拥有两个观测站,一个是可以测量目标距离和方位信息的有源雷达传感器,一个是仅能测量目标方位信息的无源传感器或者只能测量目标距离信息的激光传感器;(3)观测站不存在位置误差;(4)所有量测参数的误差均为高斯白噪声。首先介绍雷达与无源传感器的数据融合方法,它对应了三维量测与二维测向量测的融合。如图1 所示,假设雷达位于坐标系原点O,测得目标C 的距离为ra 和方位角为a(ra>0,0 设无源传感器位于点B(l,0),将雷达单次量测点C转换到传感器B 的局地极坐标系,可得到相应的距离rb和方位角b′: 由于传感器B 只能测得目标的方位信息,无法直接跟位于异地的雷达量测结果进行融合处理,故需要人为地构造一个假的二维量测点。令参数 则计算得雷达量测转换到位置B 的方位角方差为 设无源传感器B 测得目标C 的方位角为b(0 如果两个观测站重合,即传感器位于同一平台上,则有b′=a 和rb=ra,由公式(7)计算得σ′2b=σ2a,故我们的新方法对同一平台差异维度传感器数据融合是完全兼容的。 定义假量测点H(xH,yH): 令参数 则参照公式(2),H 点的协方差R 可写为 忽略协方差矩阵P 和R 之间的相关性,采用简单凸组合方法对雷达量测与假量测结果进行融合[6],得出最终的目标位置估计X: X=R[P+R]-1XC+P[ P+R]-1XH(13) 图2 雷达与激光传感器量测示意图Fig.2 Illustration of measurements obtained from radar and laser sensors 上面详细介绍了雷达传感器与异域无源传感器的数据融合方法,下面介绍雷达传感器如何与异域激光传感器进行数据融合,它对应了三维量测与一维距离量测的融合情形。如图2 所示,即将图1 中位于B 点的无源传感器换成激光传感器。设激光传感器测得目标C 的距离为r′b,标准偏差为σ′rb,此时可仅对距离rb与r′b进行协方差加权融合,具体形式如下: 类似地定义假量测点H(xH,yH): 令参数 参照公式(2),H 点的协方差R 可写为 其中,σ′2b由公式(7)给出,再依据公式(13)计算最终结果。 为了比较融合前后目标位置精度, 我们引入GDOP(Geometric Dilution of Positioning Accuracy)参量,具体定义式为 针对有源和无源传感器数据融合方法,本文设计场景一的参数分别为:l=80 km;σr=100 m;σa=7 mrad(约0.40°);σb =4 mrad(约0.23°,如红外传感器);目标位于ra=100 km;a =15°,具体情形如图3(a)所示。由雷达和无源传感器同时且相互独立地对目标按前面所设的参数各量测1 000次,然后统计雷达量测点集、无源传感器假量测点集以及最终融合后点集的分布特征,检查精度改善情况。 图3 雷达与无源传感器组合量测仿真用例Fig.3 The simulative example of the coordinated measurements with radar and passive sensors 图3(b)中的黑加号标出了雷达仿真量测1 000次的点集,其勾画出的椭圆形状由目标雷达相对位置、雷达量测精度所决定,可通过协方差矩阵P 计算得出。灰色乘号则表示传感器B 依据公式(9)得到的假量测点集,其分布是协方差矩阵P、目标相对传感器B 的位置以及传感器B 量测角度的精度共同作用的结果。图4 给出的是组合量测每次融合后的目标位置估计,可见分散程度改善了很多。依据公式(18)计算GDOP 的结果,对于单雷达量测其GDOP 值为707.1 m, 对于组合量测GDOP 为221.5 m,可见精度提高了3 倍多。 图4 雷达与无源传感器仿真1000 次量测的最终融合点集Fig.4 The 1000 estimated target positions based on radar and passive sensors′measurements 图5 雷达与激光传感器组合量测仿真用例Fig.5 The simulative example of the coordinated measurements with radar and laser sensors 针对雷达和激光传感器数据融合方法,我们选择场景二的参数分别为:l =40 km;σr=60 m;σa=5 mrad(约0.29°);σ′rb =10 m;目标位于ra =80 km;a=45°,具体情形如图5(a)所示。同样由雷达和激光传感器同时且相互独立地各量测1 000次,然后统计雷达量测点集、激光传感器假量测点集以及最终融合后点集的分布特征,比较它们的定位精度。图5(b)中的黑加号标出了雷达仿真量测1 000次的点集,灰色乘号表示得到的假量测点集,因距离量测精度高,故显得十分细长。图6 给出的是将雷达量测与假量测结果融合后的最终目标位置估计,可见密集了许多。同样依据公式(18)计算GDOP 的结果,对于单雷达量测GDOP 值为395.1 m,对于组合量测GDOP 值变为119.5 m,精度也提高到原来的3 倍多。 图6 雷达与激光传感器仿真1 000 次量测最终融合点集Fig.6 The 1 000 estimated target position based on radar and laser sensors′measurements 本文研究了差异维度传感器数据融合的问题,首先通过一定的转换规则将雷达量测的三维协方差矩阵转到缺维传感器所在平台的极坐标系下,先进行一维或二维的加权融合,得出假量测点及其协方差矩阵,再通过凸组合融合方法得出目标最终的位置估计。本文的新算法主要有以下4 个优点:一是既适用于同平台传感器,又适用于异平台传感器;二是对于异平台情形,相对于传统方法,不需要联立方程求解,从而简化了求解过程,尤其是联立方程后协方差的计算是相当复杂棘手的(如计算雅可比矩阵);三是具有通用性,无论第二个传感器是不是只有方位角量测或俯仰角量测或距离量测,或同时拥有两个角度的量测,或距离加任意一个角度的量测等,本方法均采用相同流程处理;四是合理利用了所有有用的量测信息,不存在特定情形下需要人为选择信息的问题,同时精度改善程度高于传统方法。当然,在这一点上精度具体的改善程度跟场景和传感器量测精度有很大关系,主要取决于雷达量测误差椭球与假量测点的误差椭球的形状和空间方位。这里设计了两个二维仿真场景,一个是雷达与无源测向传感器进行数据融合,另一个是雷达与激光测距传感器进行数据融合,仿真结果表明组合量测精度是单雷达量测精度的3 倍以上。相信该新方法在多传感器协同探测领域将具有相当的应用价值。 [ 1] Saha R K.Track-to-track fusion with dissimilar sensors[ J] .IEEE Transactions on Aerospace and Electronic Systems,1996,32(3):1021-1029. [ 2] Saha R K, Chang K C, Kokar M M.Fusion of synchronous[ J] .SPIE,1997,3068:206-217. [ 3] 朱志宇.基于红外和雷达数据融合的机动目标跟踪方法[ J] .激光与红外, 2007(2):170-174. ZHU Zhi-yu.Maneuver target tracking based on infrared sensor and radar data fusion[J] .Laser &Infrared,2007(2):170-174.(in Chinese) [ 4] 王毅.一种新的雷达与红外传感器异平台数据融合方法[ J] .激光与红外, 2010(3):325-329. WANG Yi.New data-fusion algorithm for radar and IR sensors at different sites[ J] .Laser &Infrared,2010(3):325-329.(in Chinese) [5] 车志宇, 熊伟,何友, 等.雷达-红外异地配置下的数据融合算法[J] .弹箭与制导学报,2005(1):385-387. CHE Zhi-Yu, XIONG Wei, HE You, et al.Data-fusion algorithm for radar and IR sensors at different sites[ J] .Journal of Projectiles Rockets Missiles and Guidance,2005(1):385-387.(in Chinese) [6] 韩崇昭, 朱洪艳, 段战胜.多源信息融合[M] .2 版.北京:清华大学出版社,2010. HAN Chong-zhao,ZHU Hong-yan,DUAN Zhan-sheng.Multisource information fusion[M] .2nd ed.Beijing:Tsinghua University Press,2010.(in Chinese)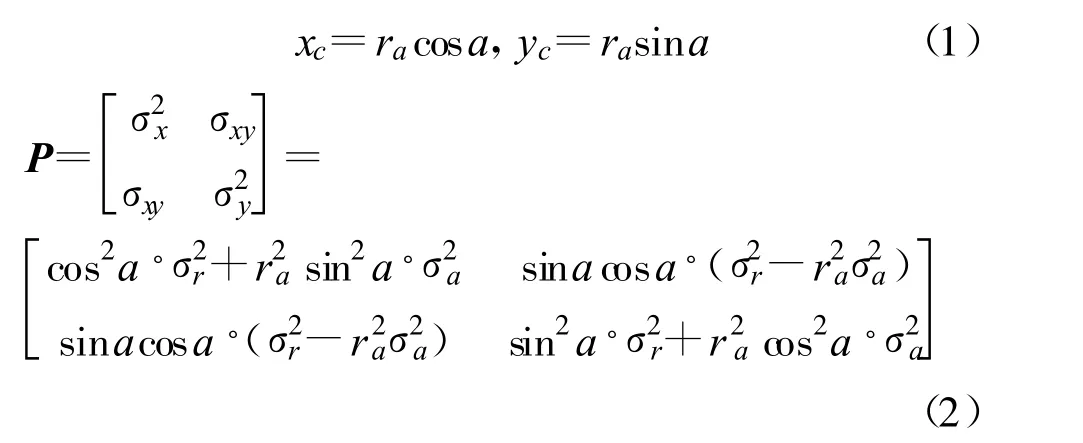
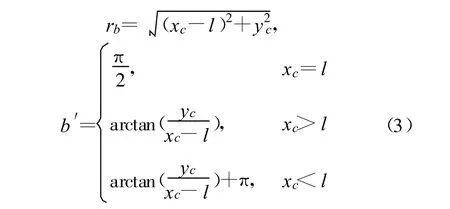
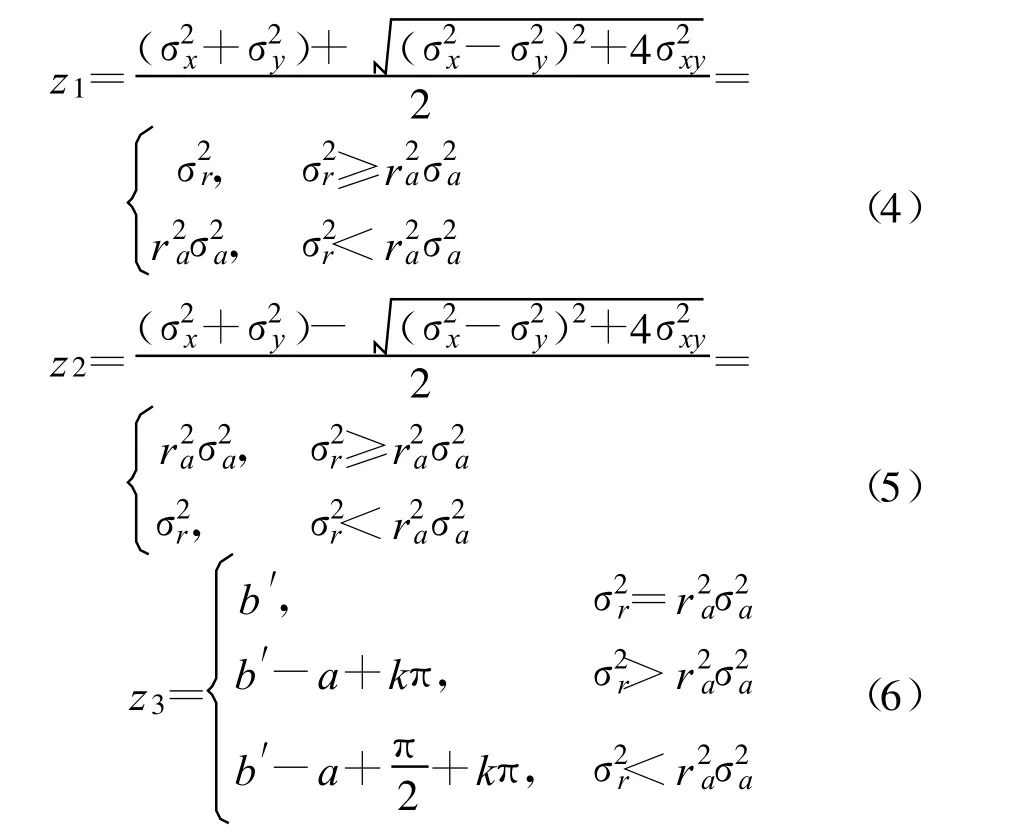
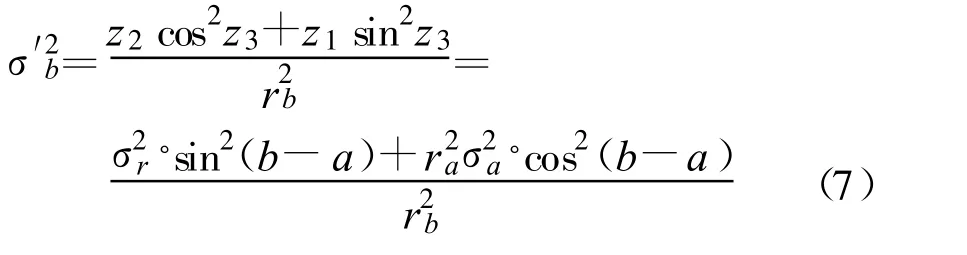
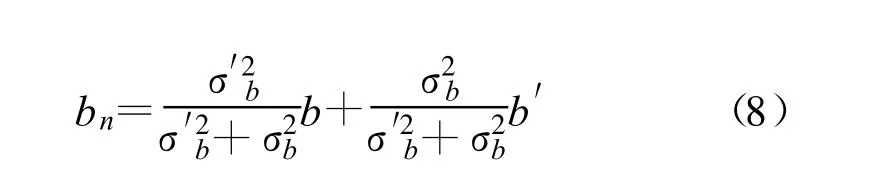
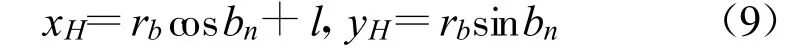
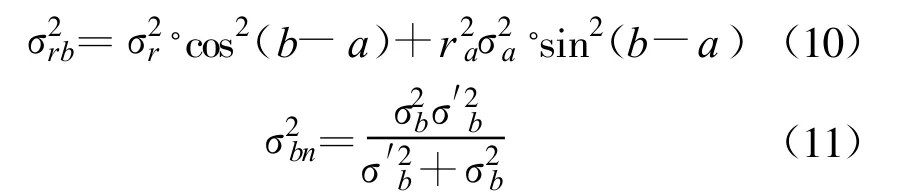
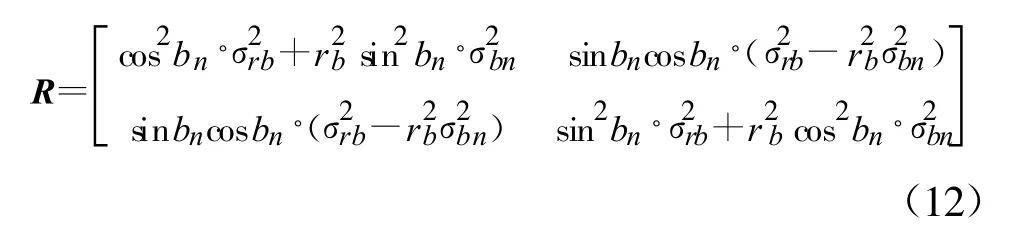
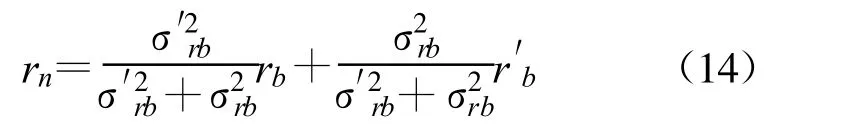
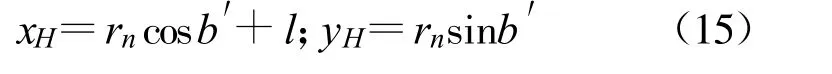
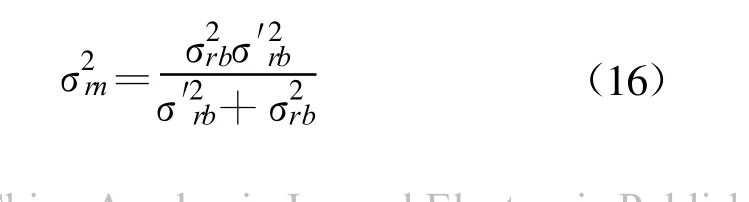
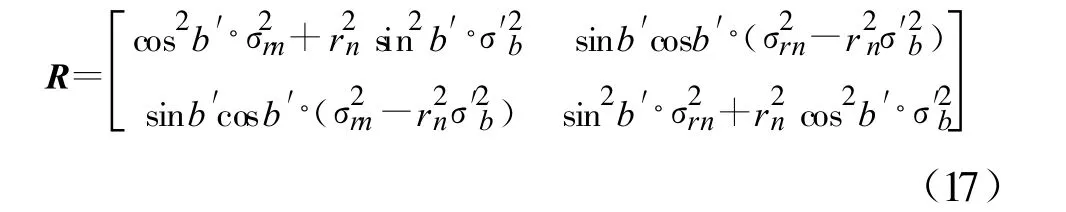
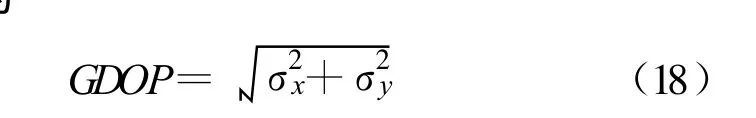
3 仿真分析
4 结 论
