不确定非线性时变时滞广义系统的保性能控制
2013-03-17阮万清张鸿艳冯玉铁
阮万清,张鸿艳,冯玉铁
(黑龙江科技学院理学院,哈尔滨150027)
0 引言
时滞是指系统现在的状态变化率依赖于过去的状态。人们把具有这种特点的系统称为时滞系统。从系统稳定性理论的角度看,大部分系统的过去状态都会对系统的当前状态产生某种程度的影响。所以,系统的时滞现象通常是使系统稳定性变坏和系统性能恶化的重要原因之一。目前,时滞系统的研究已成为控制工程领域研究的热门问题。而时滞广义系统是比正常时滞系统更能准确地描述实际动态的系统,因此人们越来越重视对时滞广义系统的研究[1-5]。文中在给定的性能指标J下,设计一个新的保性能控制器u(t)=Kx(t),从而使得原时变时滞广义系统所对应的闭环系统不仅是鲁棒渐近稳定的,且对应的性能指标满足J≤J*(即性能有上界)。
1 系统描述与基础知识
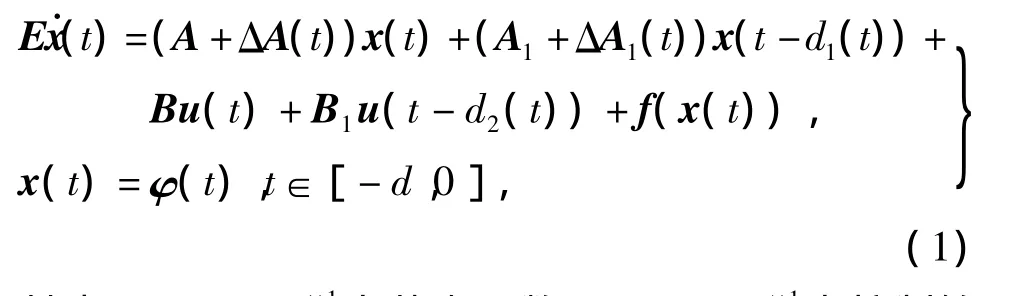
已知给定的不确定非线性时变时滞广义系统为其中,x(t)∈n×1为状态函数;u(t)∈m×1为控制输入函数;E,A,A1,B,B1分别是具有适当维数的已知常矩阵,假定E∈n×n为奇异矩阵;d1(t),d2(t)是系统的时变时滞后时间且满足0≤d1(t)≤d1,0≤d2(t)≤d2(t)≤α<1(t)≤β<1,d1(0)=a,d2(0)=b,d=max(d1(t),d2(t));φ(t)是给定的连续初始向量函数;ΔA(t)和ΔA1(t)为实有界矩阵函数且有如下的形式:
ΔA(t)=D0F0(t)E0和ΔA1(t)=D1F1(t)E1,其中,F0(t),F1(t)是时变的不确定矩阵,满足(t)F0(t)≤I,(t)F1(t)≤I,∀t∈;D0,D1,E0,E1分别是已知的常矩阵;f(x(t))满足‖f(x(t))‖≤‖Gx(t)‖,G为给定的常矩阵。
对于系统(1),给定如下性能指标:
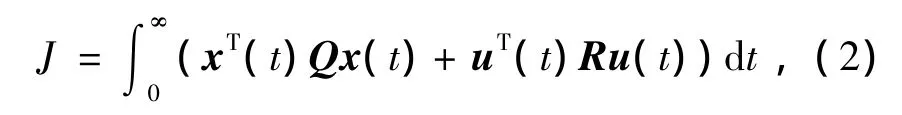
其中Q和R都是已知的正定常矩阵。
文中的任务是要设计一个新的保性能控制器:

使得系统(1)和控制器(3)所构成的闭环系统

是鲁棒渐近稳定的,并且对应的性能指标J满足J≤J*。
定义1[1]已知给定的时变时滞广义系统和给定的性能指标J,若存在一个控制器u(t)=Kx(t)和正数J*>0,使得对应的闭环系统是鲁棒渐近稳定的,且给定的性能指标满足J≤J*,则称该控制器为系统的保性能控制器,且系统的一个性能上界为J*。
引理1[2]已知Y为对称矩阵,D和E是已知的常矩阵,且FTF≤I,则Y+DFE+ETFTDT<0成立的充分必要条件为其中ε>0。
引理2[3]x和y分别为n维的实列向量,λ是不为零的实数,则有2xTy≤λ-1xTx+λyTy。
引理3[4]已知矩阵A,D,E和F是具有适当维数的实矩阵,并且满足FTF≤I,若对于任意的正定矩阵P>0和任意的非零实数μ>0,并且当P-μDDT>0时,则有(A+DFE)TP-1(A+DFE)≤AT(P-μDDT)-1A+μ-1ETE成立。
引理4[5]已知矩阵阶对
称矩阵,其中S11是r阶方阵,则S<0分别和下面的两个式子等价:
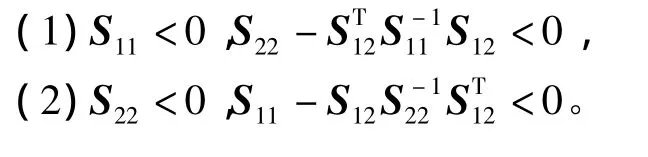
2 主要结果
定理1对于已知的时变时滞广义系统(1)和给定的性能指标(2),若能找到正定矩阵R1>0,R2>0、可逆矩阵P和具有适当维数的矩阵K,并且使得对所有允许的非线性函数f,有下面的式子成立:

其中Ω=(A+ΔA(t)+BK)TP+PT(A+ΔA(t)+BK)+KTR2K+R1+GTG+PTP,则称控制器u(t)=Kx(t)是系统(1)的一个保性能控制器,且对应的性能指标满足J≤J*=φT(0)ETPφ(0)+
证明为了证明的方便,在文中的证明过程中记x=x(t),x1=x(t-d1(t)),x2=x(t-d2(t)),u=u(t),f=f(x(t)),ΔA=ΔA(t),ΔA1=ΔA1(t),
构造如下的Lyapunov函数:
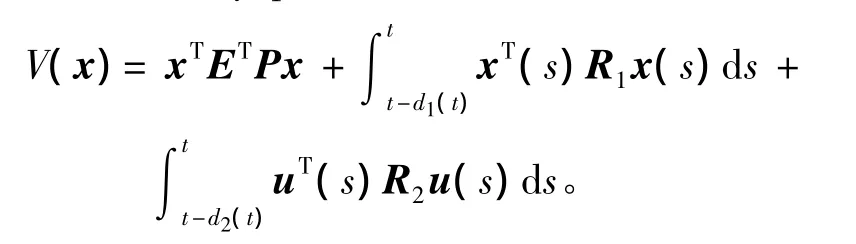
将Lyapunov函数沿着闭环系统(4)两端对t求导:
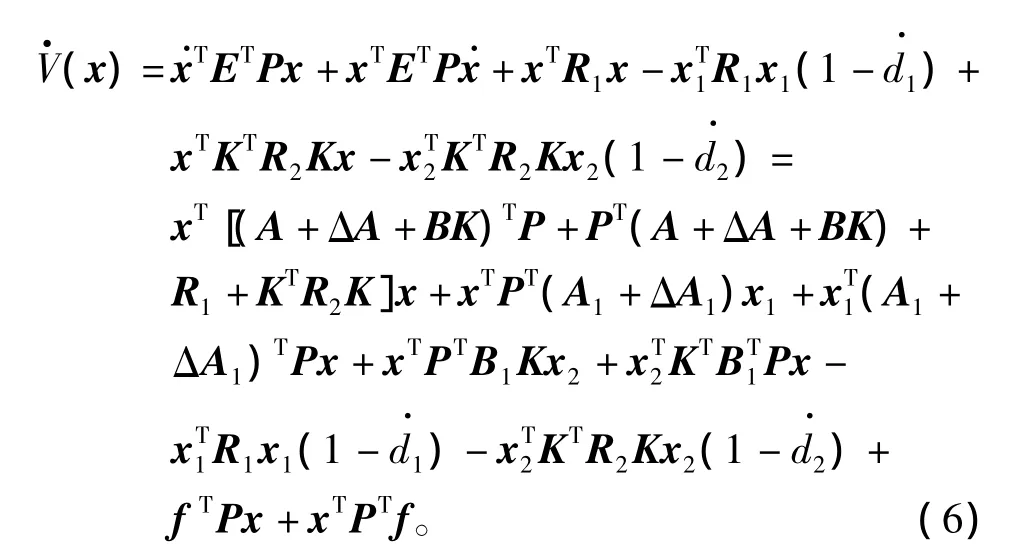
由引理2可知,
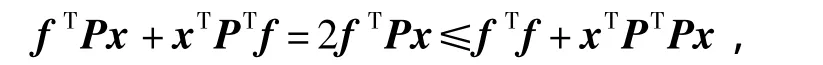
又因为

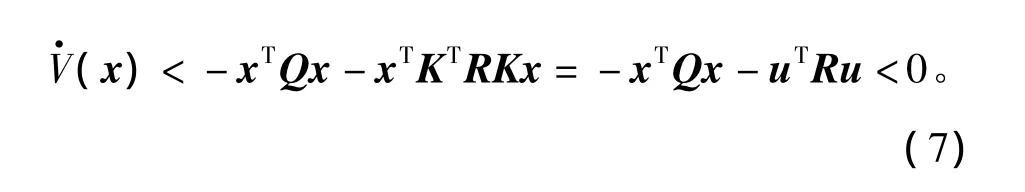
则由Lyapunov稳定性理论可知,系统(1)所对应的闭环系统(4)满足鲁棒渐近稳定。将式(7)对时间t∈[0,+∞)积分,得出V(0)=J*成立。再将初始值x(0)=φ(0)代入到J*中,得出

因此,定理1的结论成立。
定理1通过构造恰当的Lyapunov函数,给出了保性能控制器的设计方法。但是,该不等式的求解有一定的困难,因为含有不确定项。下面的定理2就给出了和定理1等价的结论,并且是一个可以利用LMI工具箱求解的线性矩阵不等式的形式。
定理2对于带有非线性函数f的时变时滞广义系统(1)和对应的性能指标(2),如果存在实数ε>0和可逆矩阵X以及适当维数的矩阵W,有下面的式子成立:
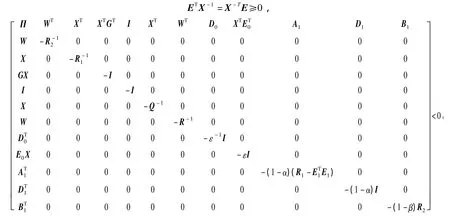
其中Π=(AX+BW)T+AX+BW,则称控制器u(t)=WX-1x(t)是已知系统(1)的一个保性能控制器,且对应的性能指标满足

证明将式(5)采用引理4等价变形为

将不确定项代入式(8),则式(8)等价变形为

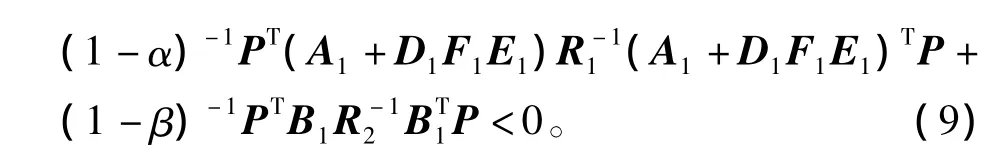
由引理1,可知

由引理3,可知
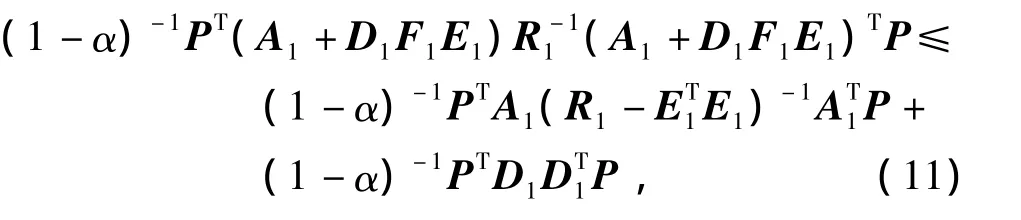
将式(10)、(11)代入式(9)中,再由引理4等价得出

其中Σ=ATP+PTA+KTBTP+PTBK,然后用矩阵diag(P-T,I,I,I,I,I,I,I,I,I,I,I)和矩阵diag(P-1,I,I,I,I,I,I,I,I,I,I,I)分别左乘和右乘式(12),再令X=P-1,W=KX,就可以得出定理2成立,且相应的性能指标满足
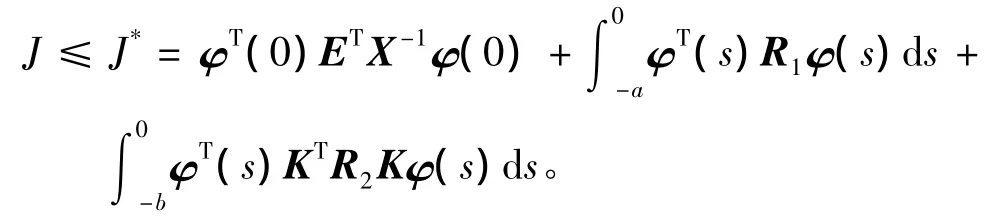
3 仿真实例
考虑时变时滞广义系统(1),其中:

利用Matlab中LMI工具箱求解得出:

数据仿真结果如图1、2所示。仿真结果表明,所设计的控制器具有鲁棒性能。
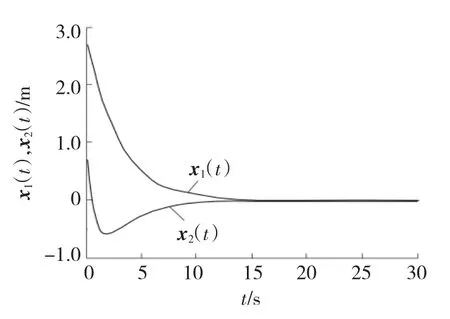
图1 系统的状态曲线x1(t),x2(t)Fig.1 State curves x1(t),x2(t)of system
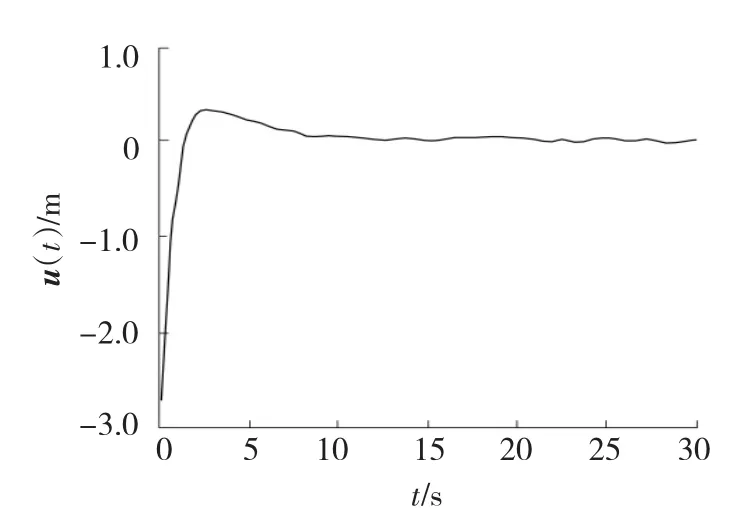
图2 系统的控制输入u(t)Fig.2 Control input u(t)of system
4 结束语
文中研究了一类参数不确定且带有非线性函数的时变时滞广义系统的保性能控制问题。创新之处在于将文献[1]的方法推广到时变时滞广义系统中,并分别将文献[2]和[3]中加入了不确定项和输入时滞后得出新的保性能控制器的设计方法。然后,将该设计方法以线性矩阵不等式的形式给出,大大简化了计算量。最后,给出仿真实例并验证了方法的可行性。
[1] 李文林,肖楠.不确定变时滞系统的非脆弱保性能H∞控制[J].清华大学学报:自然科学版,2008,48(S2):1702-1706.
[2] 焦建民,孙小军,吴保卫.不确定非线性广义时滞系统的保性能控制[J].昆明理工大学学报:理工版,2009,34(2):108-111.
[3] 尚阿曼,吴保卫,刘丽丽.带有非线性扰动的非脆弱奇异时变时滞系统的保性能控制[J].陕西科技大学学报,2012,30(2):94-99.
[4] 张金花,邢伟.不确定多时滞广义系统的非脆弱H∞保性能控制[J].吉林大学学报:理学版,2011,49(3):452-458.
[5] 俞立.鲁棒控制——线性矩阵不等式处理方法[M].北京:清华大学出版社,2002:8.
[6] 杨波,马跃超,赵静敏,等.一类带有扰动输出时滞广义系统的鲁棒H∞控制[J].河北工程大学学报:自然科学版,2008,25(1):100-103.
