求解广义凸规划的神经网络方法

杨静俐

（福州海峡职业技术学院基础教学部，福建福州350002）

求解广义凸规划的神经网络方法

杨静俐

（福州海峡职业技术学院基础教学部，福建福州350002）

提出了一种求解具有线性约束的广义凸规划的神经网络方法，其基本思想是从数值逼近的方法出发，基于Fibonacci法的基本思想，结合神经网络的结构特性，构造出一种求解广义凸规划的神经网络学习算法。此算法收敛速度快，求解精度高，对目标函数要求较低，仿真实验验证了其有效性。

广义凸规划；Fibonacci法；神经网络；学习算法

最优化问题是运筹学的一个重要组成部分，在自然科学、社会科学、生产实践中有着重要的实用价值[1]，因此，在最近40多年中得到了迅速的发展和广泛的应用，而作为运筹学中一个重要分支的数学规划，影响则更为深远。近30年来，凸性理论已广泛应用到数学规划的各个领域中[2]，但是在多种情况下，凸性对于数学规划的结果只是充分条件而不是必要条件。同时，凸分析中很多重要性质并不要求所讨论的函数是凸函数，而只需要它的水平集是凸集，即函数具有广义凸性[3]。因此，广义凸性已成为数学规划研究的一个新的发展趋势。1970年，学者B.De Finetti首先研究了水平集是凸集的函数[4]，他发现这一类函数包括所有的凸函数，同时还包含一些非凸函数。W.Fenchel[5]把这类函数定义为拟凸函数，同时比较系统地研究了它的性质。M.Slater较早的将Kuhn-Tucker鞍点等价定理推广应用于广义凸规划中，此后，从事广义凸性研究的学者逐渐多起来，并且取得了一系列重要的成果，其中比较突出的是J.A.Ferland,J.P. Crouzeix[6]和杨新民[7]等人的工作。

人工神经网络是由许多并行工作的处理单元组成的系统，它的学习功能非常强大，还具有大规模并行计算的能力[8]。因此，神经网络为优化问题的计算提供了一条非常有效的途径，并成为求解最优化问题的重要方法之一。1985年，Hopfield J.J和Tank D.W利用神经网络成功地解决了TSP问题[9]。此后，人们提出了许多神经网络模型，并将它们应用于线性和非线性规划中。然而，目前大多数学者都是研究求解凸二次规划的神经网络模型[10]，对广义凸规划的求解，尚未建立较好的神经网络模型。基于此，本文从数值逼近的方法出发，基于Fibonacci法的基本思想，并结合神经网络的结构特性，提出了求解广义凸规划的神经网络学习新算法。同时构造数值实例，对提出的神经网络算法进行了仿真实验，验证了结果的有效性。

1 预备知识

1.1 凸分析基础理论

引理1[11]设Ω∩Rn为非空凸集，f∶Ω→R，则f（x）为Ω上的拟凸函数的充要条件是：Ar∈R，水平集Hr（f）=｛x|x∈Ω，f（x）≤r｝是凸集。

注1：由于凸函数的水平集是凸集，则由引理1可知，凸函数一定是拟凸函数，而拟凸函数不一定是凸函数。如图1，f（x）是拟凸函数，但不是凸函数。

图1 拟凸函数

考虑如下优化问题：

若问题（GCP）的可行集F是凸集，f（x）是F上的（严格）拟凸函数或（严格）伪凸函数，则称问题（GCP）为广义凸规划问题。

定理1设问题（GCP）的可行集F是凸集，f（x）是F上的严格拟凸函数，则广义凸规划(GCP)的任一局部最优解x＊也是它的全局最优解。证明用反证法证明。

1.2 Fibonacci法基本思想

Fibonacci数定义如下：

从产量降低到几无经济收益时开始，到大部分植株不能正常结果以及死亡时为止。由于骨干枝，特别是主干过于衰老，更新复壮的可能性除部分果树（如某些柑桔类）外都很小，也无经济价值。应砍伐清园，另建新园。

可以用以下公式来描述：

利用Fibonacci法求解优化问题的基本思想是：确定初始搜索迭代区间[a1，b1]和迭代精度ε，在n次迭代之后，可以获得最后搜索区间[a2，b2]，且满足bn-an≤ε，则搜索区间长度的缩短率满足

根据最终区间长度的上界ε，由（2）式可以求出Fibonocci数Fn，再根据（3）式，可以确定出n，从而搜索一直进行到第n个搜索点为止。

基于Fibonacci法求解优化问题的步骤如下：

步骤1：根据决策变量的约束条件a1≤x≤b1，确定初始搜索区间为[a1，b1]，设ε＞0为允许的最后搜索区间长度，根据（2）式和（3）式可以确定n，从而得到Fn，Fn-1，Fn-2，令

令k=1；

步骤2：若|bk-ak|＜ε，计算结束，最优解x＊∈[ak-bk]，可取x＊=（bk-ak）/2，否则，令

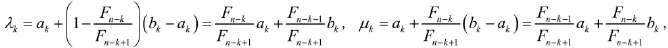
计算f（λk），f（μk），若f（λk）＞f（μk），则转步骤3，若f（λk）≤f（μk），则转步骤4；

计算f（μk）；

步骤4：令ak+1＝ak，bk+1＝μk，再令

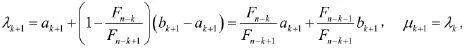
计算f（λk+1）；

步骤5：令k=k+1，返回步骤2。

2 神经网络拓扑结构

基于Fibonacci法的基本思想，本文构造如下前向神经网络，网络结构图为：

图2 基于Fibonacci法神经网络的拓扑结构图

文中符号表示为：

Ni,j：第i层的第j个神经元，i＝0为输入层；neti,j：神经元Ni,j的输入值；Oi,j：神经元Ni,j的输出值；

ω（i,j）（k,l）：神经元Ni,j与神经元Nk,l的连接权值；阈值向量：θ＝0。

本文构造了一个包含1个输入层、3个隐含层、1个输出层和1个反馈层的6层神经网络。图2构造的神经网络计算步骤为：

(Ⅰ)输入层：将迭代区间[ak,bk]的两端点作为神经网络的输入，N0,1与N0,2对应的输入分别为：

（Ⅴ）迭代：将输出神经元同时作为反馈部分的输入，若f（λk）＞f（μk），则ak+1＝λk，ak+1=bk，否则，若f（λk）≥f（μk），则令ak+1＝λk，bk+1＝μk。令k=1，k=k+1，循环，直到满足要求的精度为止。

3 神经网络学习算法

对于具有线性约束的广义凸规划问题，利用上文构造的神经网络模型，提出的学习算法如下：

步骤1：根据约束条件，可以求出x的上界和下界，记为a1，b1，令网络的初始输入net0,1=a1，net0,2=b1，并给出迭代精度ε＞0，若｜b1-a1｜＜ε，则令最优解x＊＝（a1+b1)/2，否则，取初始点x（0）=（a1+b1)，进行下面步骤；

图3 f（x1，x2)=-x1，x2的图形

根据引理3可以判断，目标函数f（x1，x2)不是凸函数，而是拟凸函数。利用Matlab工具箱中quadprog命令求解，得理论最优解为x*[2.0，3.0]T，理论最优值为f*=-6。

利用文中构造的神经网络模型求解，用Matlab软件编程，令神经网络的初始输入为x（0）=[1，2.5]T，取ε＝10－4，经过20次迭代，得近似最优解x*＝[1.999，3.000]T，近似最优值为f*=-5.9997。决策变量的迭代收敛路径如图4：

图4 x 1,x2的迭代收敛变化路径

5 结论

本文结合Fibonacci的基本思想，利用神经网络的结构特性，提出了一种求解具有线性约束广义凸规划的神经网络模型，此模型对具有双边约束的线性规划问题同样适用。而且随着优化问题维数的不断升高，神经网络学习算法的优越性越发明显。

[1]HorstR,Pardalos PM,ThoaiNV.Introduction toglobaloptimization[M].Kluwer Academic Publisher,Chap 1-6,2000.

[2]杜廷松,费浦生,蹇继贵.非凸二次规划全局极小问题的新型分枝定界算法[J].计算机工程与应用,2008,44(17):49-52.

[3]Stephem Boyd,Lieven Vandenberghe.Convex optimization[M].Cambridgeuniversity press.2004.

[4]Greenberg H J,PierskallaW P.A review ofquasi-convex function[J].OR,1971,19:1553-1570.

[5]FenchelW.Convex cones,setand functions[J].Princeton University,Princeton New Jersey,1951.

[6]Crouzeix JP,Ferland JA.Criteria for quasi-convexity and pseudoconvexity:ralationship and comparison[J]s.Math prog.1982,23: 193-205.

[7]Yang XM.A noteon criteriaofquasiconvex functiom[J].运筹学学报.2001,5(2):55-56.

[8]Xia Y S,Feng G,Wang J.A recurrentneuralnetwork with exponential convergence for solving convex quadratic program and related linear piecewiseequation[J].NeuralNetworks,2004,17:1003-1015.

[9]Hopfield JJ,Tank DW.Neuralcomputation ofdecisions in optimi-zation problems[J].Biol.Cybern,1985,52:141-152.

[10]杨静俐,杜廷松.求解线性约束的二次规划神经网络学习新算法[J].计算机工程与应用,2010(24):37-39,192.

O224

A

1673-8535(2013)06-0047-06

杨静俐（1983-）,女，湖北荆门人，福州海峡职业技术学院教师，研究方向：优化理论与算法、神经网络及其应用。

（责任编辑：高坚）

2013-09-30