基于Ring-Barrier相位的交叉口车道功能判分与信号配时协同优化模型

张 鹏 李文权 常玉林

(1 江苏大学汽车与交通工程学院，镇江212013)

(2 东南大学交通学院，南京210096)

信号交叉口进口车道功能的划分、相位的选择 和配时三者之间是相互影响的，采用个人经验或者不断尝试的方法难以保证得到最优的交叉口控制效果.因此，学者们尝试对信号交叉口的时空资源协同优化进行研究.Lam 等［1］以流量比之和最小为目标，建立了车道功能划分和信号配时的组合优化模型，结果表明，交叉口的性能会有一定程度的提高，但是流量比之和最小化未必能使交叉口总延误最小.钟章建等［2］以车均延误最小为优化目标，建立了车道划分和信号配时优化模型，但仅针对交叉口的一个进口为研究对象.王京元［3］提出了一种经验方法来优化车道设置和配时，虽然方法简单，但实用效果严重依赖个人经验.曾滢等［4］建立了动态车道功能与信号相位组合模型，并用Visual Basic 语言编制程序对该模型进行求解，但是车道组合方案、相位方案和信号配时是分开进行优化的，难以保证结果最优.马万经等［5］基于Ring-Barrier 相位，以交叉口公交车延误和交叉口社会车流延误为目标，提出了一种基于车道的单点交叉口公交被动优先控制多目标优化模型，但是在车道设置的优化上没有考虑共用车道(如直左车道)的情况.Wong 等［6-9］提出了一种基于车道的信号配时优化方法，分别建立了备用通行能力最大、周期最短、延误最小以及多时段的车道设置和配时优化模型，可以产生较好的优化效果，但是模型中动辄上千的变量和约束条件使建模、求解以及实际应用都存在很大的困难.

本文基于Ring-Barrier 相位模式，建立了一种交叉口进口车道功能划分和信号配时协同优化模型.该模型是一个常规的整数非线性规划模型，目标函数取车均延误最小，整数变量是交叉口各个进口不同转向运动的车道数量(允许共用车道)，连续变量包括周期时长、绿灯分配等.应用分支定界法求解，并实地调查了南京市的一个交叉口进行计算分析.

1 模型建立

考虑一个十字型交叉口(见图1)，采用Ring-Barrier 相位结构［10］(见图2).图1中，数字1～4表示交叉口的4 个进口.图2中，L，R，T 分别表示左转、右转、直行车流.例如，3L 表示交叉口进口3(i=3)的左转车流，4R 表示交叉口进口4(i =4)的右转车流.与传统的双向左转四相位不同，Ring-Barrier 相位可以灵活搭接，同环且同段的一对相位可以互换位置(如相位3L 和1T 可以互换位置).根据实践经验，本文取各个相位之间的绿灯间隔时间相同，可以得出如下等式:

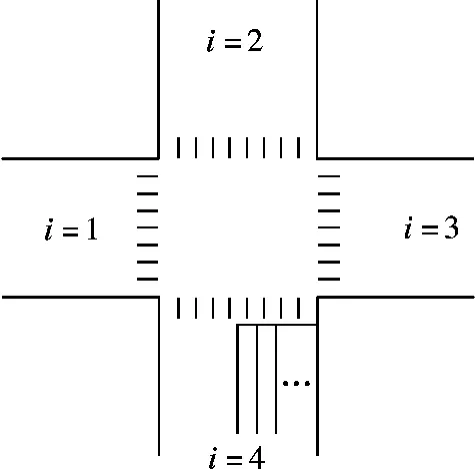
图1 交叉口进出口编号示意图

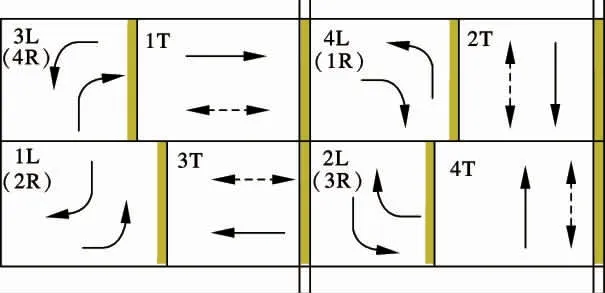
图2 Ring-Barrier 的相位模式

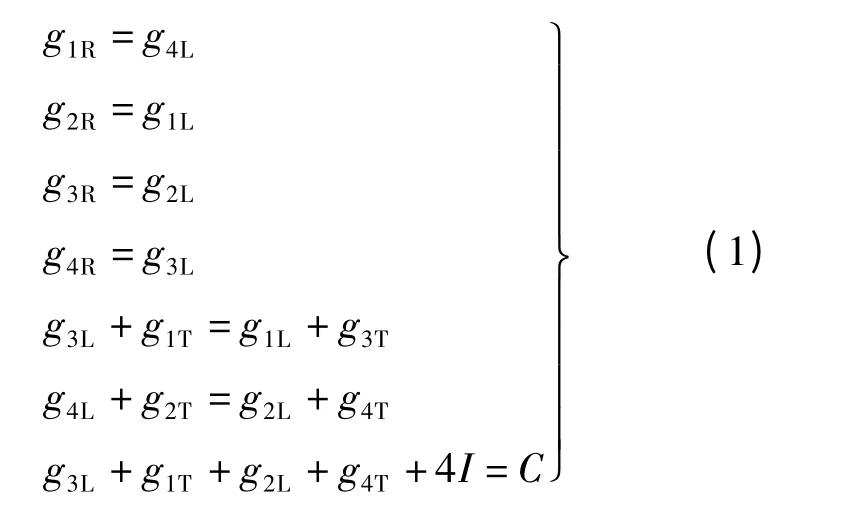
式中，giR，giL，giT分别为进口i 右转、左转、直行车流的显示绿灯时间，且i =1，2，3，4;I 为相位间隔时间;C 为周期时长.

在交叉口进口i 处，车道类型可以是左转专用、直行专用、右转专用和直左共用.考虑行人安全，本模型不采用直行右转共用车道，则

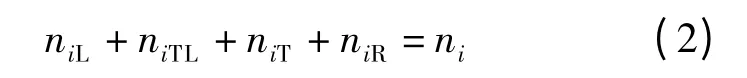
式中，niL，niT，niR，niTL分别为进口i 的左转专用、直行专用、右转专用和直左共用车道数;ni为进口i的总进口车道数.

一旦进口i 设置为直左共用车道(即niTL＞0)，则该进口的直行车流和左转车流应当同时放行，即

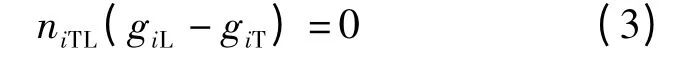
为避免左转车流和直行车流的冲突，各进口直左共用车道数目不应超过1 条，即

交叉口出口i 的出口车道数应不小于各转向到达车流所在进口道分配的车道数，即

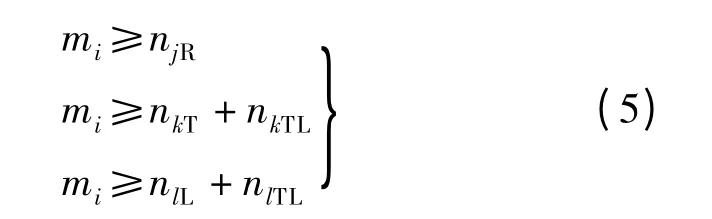
式中，mi为出口i 的出口车道数.如图1所示，当i=1 时，进口2 的右转车道数(n2R)不能超过mi，即j =2;进口3 的直行车道数与直左车道数之和(n3T+n3TL)不能超过mi，即k=3;进口4 的左转车道数与直左车道数之和(n4L+n4TL)不能超过mi，即l =4.同理可得:当i =2 时，j =3，k =4，l =1;当i =3时，j =4，k=1，l=2;当i=4 时，j =1，k=2，l=3.

进口i 左转车道组的通行能力不仅包括左转专用车道的通行能力，还包括部分直左共用车道的通行能力(由左转车辆所占比例确定).如果进口i设置有直左共用车道，则根据排队理论，直行专用车道、左转专用车道和直左共用车道的饱和度应该相同.由于这时左转和直行车流的绿灯时间是相同的，故只需满足直行车道、左转车道和直左车道的流量比相同，即

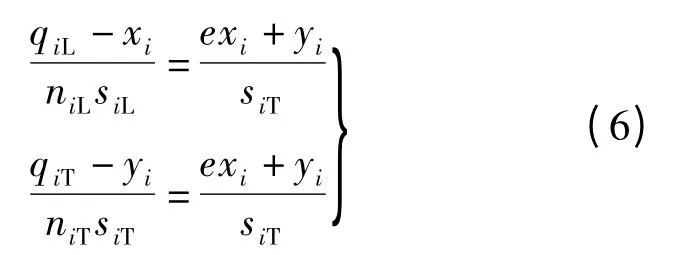
式中，qiL，qiT分别为交叉口进口i 左转车、直行车的小时流量;siL，siT分别为交叉口进口i 左转车、直行车的饱和流率;xi，yi分别为交叉口进口i 的直左共用车道中左转车、直行车的小时流量;e =siT/siL为左转小车对直行小车的折算系数.

根据式(6)，可以得到

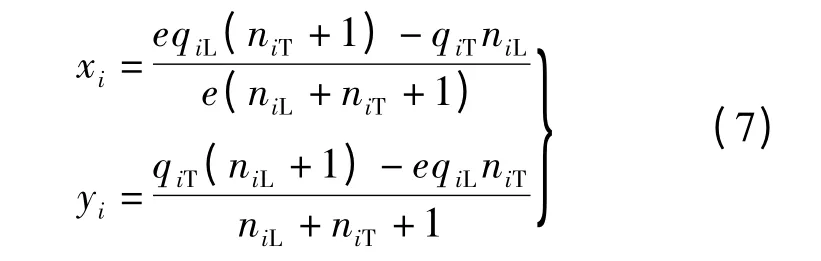
由此可知，进口i 左转车道组、直行车道组的通行能力分别为

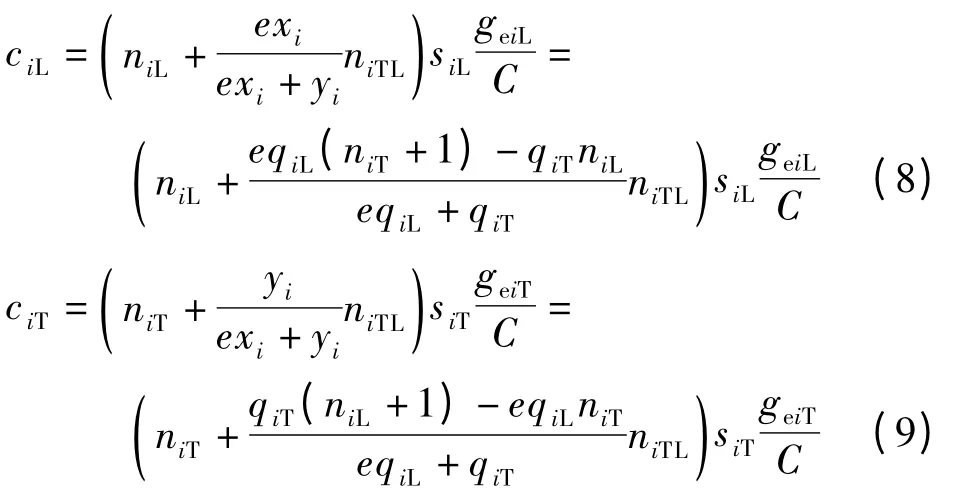
式中，geiL，geiT分别为进口i 左转车流和直行车流的有效绿灯时间.

如果设置了直左车道，则xi，yi都应大于0，即

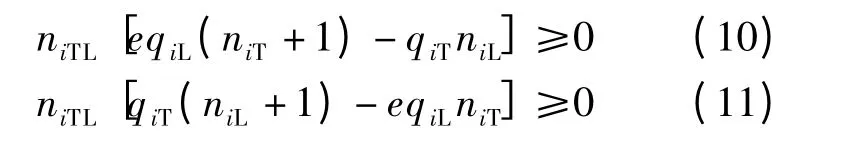
右转车道组的通行能力为

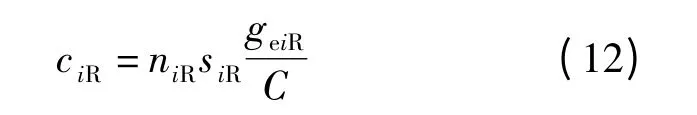
式中，geiR为进口i 右转车流的有效绿灯时间.

行人随同向直行车流一起通行.因此，直行车流绿灯必须满足行人通行最短绿灯时间，即

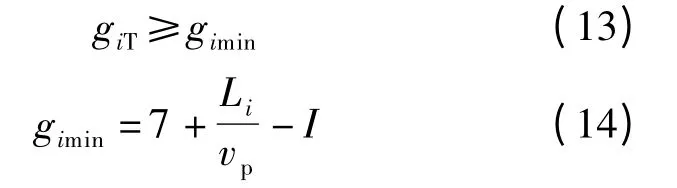
式中，gimin为进口i 直行车流右侧人行横道的行人最短绿灯时间;Li为进口i 直行车流右侧人行横道的长度;vp为行人平均过街速度.

各种转向车道的饱和度不超过0.95，即

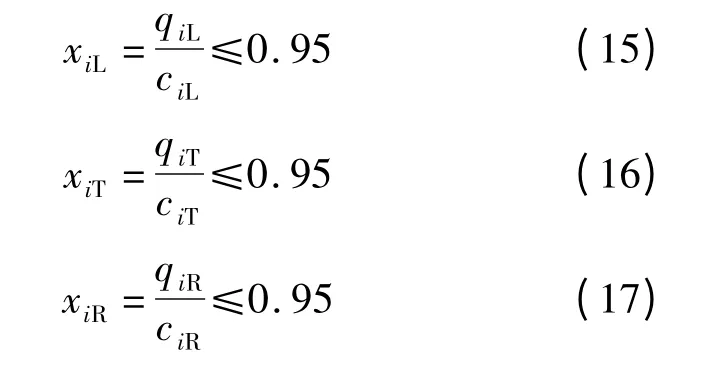
式中，xiL，xiT，xiR分别为进口i 左转、直行、右转车道的饱和度.

有效绿灯时间和显示绿灯时间之间的关系为

式中，g 为显示绿灯时间;ge为有效绿灯时间;A 为黄灯时间;l 为启动损失时间.

延误采用美国道路通行能力手册［11］推荐的公式，以左转车道组的平均延误diL为例(饱和度小于1)，有

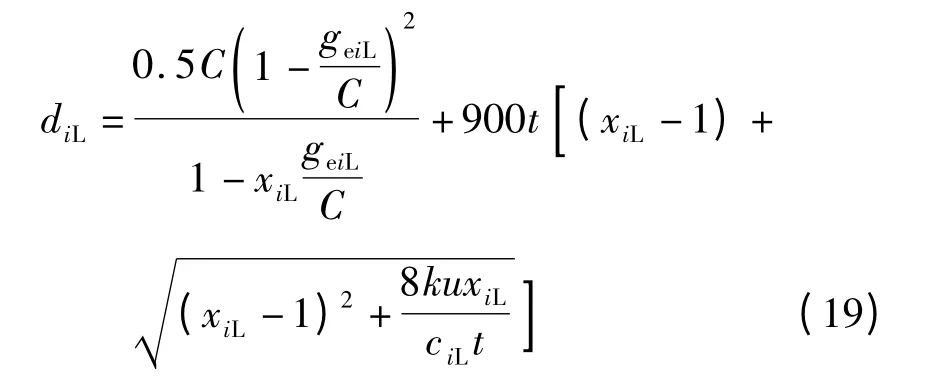
式中，t 为分析期，一般取0.25;k 为修正系数，定时控制交叉口取0.5;u 为修正系数，独立信号交叉口取1.

目标函数取交叉口的平均延误最小，即

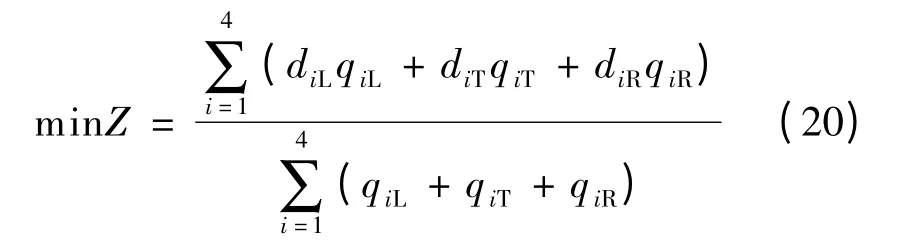
式中，diT，diR分别为进口i 右转车道、直行车道的平均延误.

2 求解算法

本文建立的模型是一个常规的整数非线性规划问题，而且模型中整数变量只有16 个.因此，本文采用分支定界的方法求解，算法描述如下.

①将本文建立的整数规划问题称作问题A，不作整数要求对应的非线性问题称作问题B.求解问题B(非线性规划解法较为成熟)，可能得到以下情况之一:

a)B 没有可行解，此时A 也没有可行解;

b)B 有最优解，并符合问题A 的整数条件，则B 的最优解即为A 的最优解;

c)B 有最优解，但不符合整数条件，记它的目标函数值为问题的下界Zbottom.

②采用常规的等流量比原则分配车道数，计算本文建立的非线性规划模型.将得到的目标函数值记为问题的上界Ztop，如果Zbottom=Ztop，结束算法;否则，进入步骤③.

③在B 下界对应的分支中选择一个不符合整数的变量进行构造约束条件，得到2 个后续规划问题，不考虑整数约束，分别求解这2 个后续问题.

④从已经符合整数条件的各分支中，选择最大的目标函数值作为新的上界Ztop;从所有的分支中，选择最小的目标函数值作为新的下界Zbottom.如果Zbottom=Ztop，结束算法;否则，进入步骤⑤.

⑤在各分支的最优目标函数值中，如有大于Ztop者，则剪掉这一支，以后不再考虑.重复步骤③，直到Zbottom=Ztop，即得到问题的最优解Ztop.

3 算例分析

为验证本文模型的效果，选取南京市一个较为繁忙的信号交叉口作为研究对象.经调查，晚高峰1 h 内的平均交通需求见表1，现状的车道设置情况(记为车道方案Ⅰ)见图3.交叉口一个直行车道的饱和流率分别为1 800，1 650，1 600 pcu/h.交叉口现状采用的是传统的双向左转四相位，周期为172 s，总的信号损失时间为12 s，详细参数见表2中配时方案1.如图4所示，水平、竖直方向过街行人的最短过街绿灯时间分别为25 和23 s.

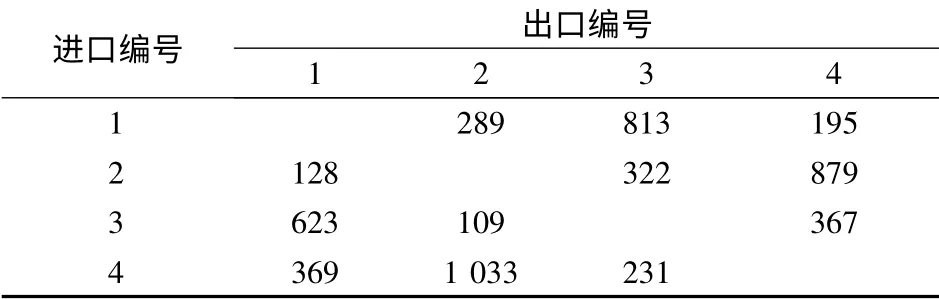
表1 路口的交通量 pcu/h

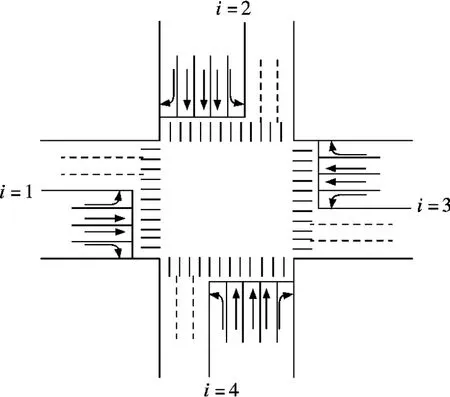
图3 现状的交叉口进口车道设置图示

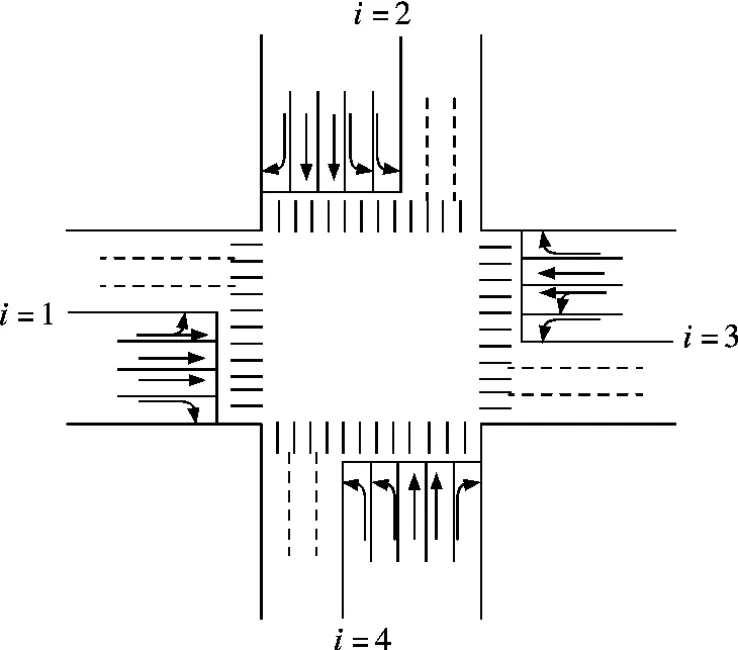
图4 优化的交叉口进口车道设置图示

首先，不改变现有的车道设置和信号相位，只对周期和绿信比进行优化，得到的信号配时结果见表2中配时方案2.

表2 信号配时方案及交叉口延误 s

然后，采用本文模型进行优化计算，经过19 次分支、共39 次非线性规划的求解运算，得到了新的车道设置方案(见图4，记为车道方案Ⅱ)和信号配时方案(见表2中的配时方案3).

最后，利用VISSIM 软件进行仿真分析，仿真截图见图5.每种方案进行6 次仿真，取平均值，得到车辆的平均延误，以比较各个方案的配时效果(见表3).

图5 仿真运行时的截图

由表2可知，与方案1 相比，方案2 的周期时长缩短了40.68 s(23.65%)，平均延误减少了13.82 s(20.10%);与方案2 相比，方案3 的周期时长进一步缩短了23.83 s(18.15%)，平均延误进一步减少了10.99 s(20.01%).由此可见，本文模型的优化效果明显.

传统的观点认为，交叉口车道的分配要符合等流量比原则，才会使车流延误较小.然而，由表3可知，无论是流量比的加权平均值还是方差，方案Ⅰ都小于方案Ⅱ，即渠划方案Ⅰ更符合车道分配的等流量比原则.但是，方案Ⅱ可以使车流延误更小.

表3 交叉口车道划分方案

4 结论

1)与传统的双向左转四相位相比，Ring-Barrier 相位模式的相位搭接更为灵活.基于Ring-Barrier 相位模式的交叉口信号配时效果优于传统的相位模型.

2)采用等流量比原则进行交叉口进口车道功能划分并不一定会使交叉口车均延误最小.

3)进口车道功能划分、相位选择和信号配时三者之间是相互影响的.因此，针对其中任何一方进行优化都难以保证得到最优的交叉口设计结果.本文模型可以显著降低信号交叉口的平均延误，缩短周期时长.

4)本文模型是一种常规的非线性整数规划模型，整数变量较少，可以用常规的分支定界法求解，计算量小，方便实际应用.

References)

［1］Lam W H K，Poon A C K，Mung G K S.Integrated model for lane-use and signal-phase designs［J］.Journal of Transportation Engineering，1997，123(2):114-122.

［2］钟章建，马万经，龙科军.信号交叉口车道功能动态划分优化模型［J］.交通与计算机，2008，26(1):15-18.

Zhong Zhangjian，Ma Wanjing，Long Kejun.An optimization model of dynamic lane assignment at signalized intersection［J］.China Computer and Communications，2008，26(1):15-18.(in Chinese)

［3］王京元.信号交叉口时空资源综合优化实用方法研究［D］.南京:东南大学交通学院，2006.

［4］曾滢，杨晓光，马莹莹.交叉口动态车道功能与信号控制协同问题研究［J］.同济大学学报:自然科学版，2009，37(7):903-908.

Zeng Ying，Yang Xiaoguang，Ma Yingying.Study on synergy problem of dynamic lane-use assignment and signal control at intersections［J］.Journal of Tongji University:Natural Science，2009，37(7):903-908.(in Chinese)

［5］马万经，杨晓光.基于车道的单点交叉口公交被动优先控制模型［J］.中国公路学报，2010，23(5):96-101.

Ma Wanjing，Yang Xiaoguang.Lane based optimization model of passive bus priority control for isolated intersection［J］.China Journal of Highway and Transport，2010，23(5):96-101.(in Chinese)

［6］Wong C K，Wong S C.Lane-based optimization of signal timings for isolated junctions［J］.Transportation Research Part B:Methodological，2003，37(1):63-84.

［7］Wong C K，Wong S C.A lane-based optimization method for minimizing delay at isolated signal-controlled junctions［J］.Journal of Mathematical Modeling and Algorithms，2003，2(4):379-406.

［8］Wong C K，Wong S C，Tong C O.The advantages of the multi-period lane-based optimization method for traffic signal design［C］//Proceedings of the Eastern Asia Society for Transportation Studies.Bangkok，Thailand，2005:1358-1366.

［9］Wong C K，Heydecker B G.Optimal allocation of turns to lanes at an isolated signal-controlled junction［J］.Transportation Research Part B: Methodological，2011，45(4):667-681.

［10］Koonce P，Lee R，Lee K，et al.Traffic signal timing manual［R］.Washington DC，USA:Federal Highway Administration，2008.

［11］Transportation Research Board.Highway capacity manual［M］.Washington DC，USA:National Research Council，2000:19-22.