一维XXZ环形自旋链中的量子关联

谭小东，高 微

（温州大学物理与电子信息工程学院，浙江温州 325035）

一维XXZ环形自旋链中的量子关联

谭小东，高 微

（温州大学物理与电子信息工程学院，浙江温州 325035）

研究了系统尺度L = 8的一维XXZ环形自旋链中的两体和多体量子纠缠以及两体量子失协，在这个过程中，充分考虑了温度和粒子间隔对纠缠和量子失谐的影响．结果发现，同种情况下，三体和四体纠缠比两体的更加“强壮”，且在低温条件下，利用多体纠缠可以探测到系统发生量子相变的临界点．与纠缠相比，量子失谐可以在较高温度下存在，且在相变点处总是表现出尖峰行为，这使得量子失谐在探测相变点方面更具优越性．

XXZ自旋链；量子纠缠；量子失协；量子关联；量子相变

量子纠缠，或者说由态叠加原理带来的两个或多个量子态之间的相干性，是量子力学最不同于经典力学的概念，它反映了量子理论的本质——相干性、或然性和空间的非定域性．随着量子理论的不断发展，量子信息论作为一门新的学科应运而生，纠缠成了量子通信、量子计算方面的重要资源．诸多经典方案不能完成的任务都可以通过量子纠缠辅助实现，例如：量子隐形传态[1]、量子密码术[2]、量子稠密编码[3]等．近年来，自旋系统在量子信息方面显示出广阔的应用前景．目前，海森堡模型已经用于模拟量子计算机的研究中，而且海森堡模型本身就可以在量子点系统、原子核自旋系统、电子自旋和光晶格等许多物理系统中实现．另外，量子纠缠与量子力学中的许多基本问题有着密切的联系，如量子相变[4]．量子相变是发生在绝对零度的一种纯量子现象，由系统哈密顿量中的耦合常数或外参数（如磁场）的改变所引发，由不确定性原理导致的量子波动所驱动，通常由一些表征系统特性的物理量，如基态能、磁化率、纠缠、量子失谐（Quantum Discord，简称QD）等的极值以及它们的一阶或二阶导数的行为来探测相变点．2002年Osterloh等人的开创性工作首先将量子纠缠与量子相变联系起来[5]．文献[6]通过研究处于基态下的XY自旋链中的最近邻和次最近邻的两个自旋粒子之间的共生纠缠度（concurrence）[6]，发现量子纠缠在系统的相变点附近存在标度行为，从此掀起了人们研究自旋链中的量子纠缠的热潮．对于自旋链中的两体基态纠缠[7-9]、两体热纠缠[10-12]以及量子纠缠与量子相变的关系[13-14]，人们已经有了比较深入的了解，但对于大系统自旋链中的连续块[15-18]或非连续块[19-21]之间的纠缠的研究基本上都停留在基态，对于热平衡态的研究相对较少，所以这也就成了近年来大家关注的焦点．

随着量子信息论的发展，很多工作已经指出，包括纠缠和非纠缠的量子关联比纠缠更基础，更广泛．纠缠只是作为一种特殊的量子关联而存在．更进一步，人们又发现纠缠为零的可分离态中含有非零的量子关联[22-23]，且这种非纠缠的量子关联已经在理论上被用在量子计算模型中[24]，一些计算方案已经在实验上得到实现[25]．QD[23]作为量子体系中总的非经典关联的度量，一经提出立刻引起了广泛的关注．人们已经证明，几乎所有的量子态都含有量子失协[26]．更令人振奋的是，中国科技大学首次完成了量子关联和经典关联在噪声环境下的演化实验研究[27]，这项成果将极大地推动量子关联的物理学研究及其应用．另外，量子失谐在一些基本的物理问题中也起到重要的作用，如海森堡自旋链中的量子相变[28-30]．Werlang等人首先将有限温度下的两体量子失谐（简称TQD）与量子相变联系起来[30]，发现TQD不仅可以在较高的温度下存在，而且在相变点附近总是表现出尖峰行为，这使得TQD在探测系统的相变点方面更具优越性．

本文受block-block纠缠的启发，在充分考虑自旋粒子间的间隔和温度对纠缠的影响的前提下，研究了系统尺度L = 8的一维XXZ环形自旋链中两体和多体（三、四体）的热纠缠，并在Werlang[30]等人工作的基础上，进一步研究了非紧邻的两体TQD，结果表明，根据TQD依然可以探测到系统的相变点，而且它抗击温度影响的能力远比热纠缠强．另外，利用多体热纠缠（特别是四体纠缠），在低温条件下，也可以探测到系统的一个相变点Δ=-1．

1 量子关联的度量

XXZ模型的系统哈密顿量为：

处于热平衡态下的正则系综是一个混合态，其状态可用密度矩阵表示：

量子纠缠是Vi da l和We r ne r根据Pe r es可分离判据，提出的两体系统任意混合态的一种纠缠度量[3 1]．实际上，它不仅适用于两体系统，对于高维多体量子态同样适用①．我们可以用量子纠缠来考察多体量子态的任意两部分的纠缠性质．对于由A、B两子系统组成的两体混态ρAB，量子纠缠一般是这样定义的：

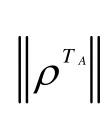
量子失谐最先是由Ollivier和Zurek两人提出的[23]，它可以作为量子系统中总的非经典关联的一种度量．两体系统的量子失谐的定义：

则量子失谐为[30-31,33]：

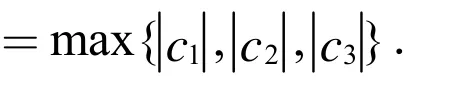
2 量子纠缠

这一部分主要研究了有限温度下，尺度L = 8的XXZ环形自旋链中的量子纠缠．在各向异性参数取Δ∈[-2, 2]的情况下，计算了两体和多体的量子纠缠．不同温度下，两体和多体的量子纠缠随各向异性参数Δ的变化曲线分别见图1、图2和图3．

2.1 两体纠缠

从图1①中可以看到，在同一温度下最近邻的两个自旋粒子间的纠缠比较“强壮”．在低温条件下（kT = 0.1），间隔最大的两体量子纠缠依然存在，并且随着两粒子间隔的增大而减小，而当

图1 不同温度下的两体量子纠缠随各向异性参数Δ的变化曲线

① 抹去环境, 本文所研究的系统由A和B两部分组成. 为了行文方便, 本文所有图中表示属于子系统A的自旋粒子,示属于子系统B的自旋粒子,表示环境.kT ≥ 1.0时，量子纠缠则在整个区间上完全消失．另外，从图1中还可以看到，当kT = 0.1时，间隔最大的两体量子纠缠被约束在了-1 ＜Δ＜ 0这个区间内，并且随Δ的变化比较剧烈．

2.2 三体纠缠

图2展示了三体纠缠的情况．与两体纠缠的情况类似，三体纠缠中非最近邻的两个连续块或非连续块之间的量子纠缠只有在低温下才不为零，并且也被约束在了-1＜△＜ 0这个区间内，但与图1中相应的曲线比较，就会发现，相同条件下，三体纠缠比两体纠缠更加“强壮”．

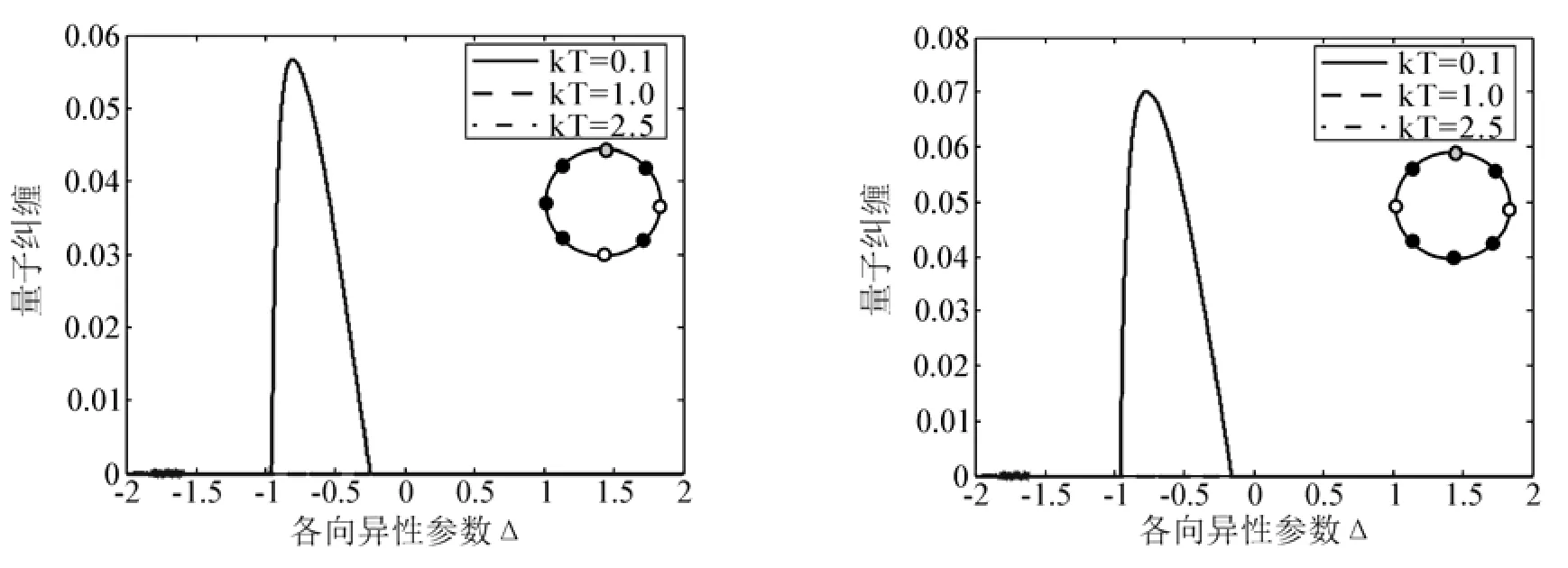
图2 不同温度下的三体量子纠缠随各向异性参数Δ的变化曲线

2.3 四体纠缠

模式一：四体态由A，B两部分组成，其中子系统A含有一个自旋粒子，子系统B含有三个自旋粒子．纠缠情况见图3（a）．模式二：四体态由A、B两部分组成，其中子系统A和B各自含有两个自旋粒子，但A和B之间无交错．纠缠情况见图3（b）．模式三：四体态由A、B两部分组成，其中子系统A和B各自含有两个自旋粒子，且A和B之间相互交错．纠缠情况见图3（c）．

四体纠缠呈现出了更多新的特点：同种情况下，四体纠缠比三体纠缠更加“强壮”，并且四体纠缠抗“热噪声”影响的能力明显增强；与两体和三体纠缠相比，在子系统A和B非最近邻的情况下，四体量子纠缠大于零的范围可以扩展到区间Δ∈[-1, 2]；当间隔均匀时，四体量子纠缠总是在Δ= 0处突然消失，见图3（a）– 3（c）中的小插图，而Δ= 0时恰好对应XX模型．从图1和图2可看出，两体和三体的量子纠缠在Δ∈[-2, -1]这个区间上都等于零，但有趣的是四体量子纠缠首度在Δ=-1的左侧出现了非零值，且在Δ=-1处表现出尖峰行为，见图3（b）– 3（c）．众所周知Δ=-1和Δ=1是绝对零度下的XXZ模型的两个相变点[34]，这里利用四体量子纠缠在低温条件下（kT = 0.1）也探测到了Δ=-1这个相变点，但是在四体纠缠的范围内，尽管我们考虑了各种情况（限于文章的篇幅，这里没有一一列出相应的曲线图），还是探测不到Δ=1这个相变点．对于XXZ模型而言，也许Δ=1这个临界点只有在更高维的多体量子态中才能用量子纠缠探测到，或许通过其它物理量才能探测到．因此，这也是一个值得探究的问题．

3 量子失谐（QD）

不同温度下的两体QD随各向异性参数Δ的变化见图4．从图4可以看到，无论是利用最近邻的两体QD，还是利用非最近邻的两体QD都可以清晰地探测到系统发生量子相变的临界点．从图像上能直观地看到QD在Δ=-1和Δ=1表现出尖峰行为．另外，通过比较发现，温度对两体量子纠缠只起抑制和消弱作用，而两体QD与温度的关系较为复杂，消弱和促进作用同时存在．与两体量子纠缠类似，QD随着两粒子间隔的增大而减小，但是低温环境下（kT = 0.1），QD在Δ=-1处基本不受粒子间隔的影响．

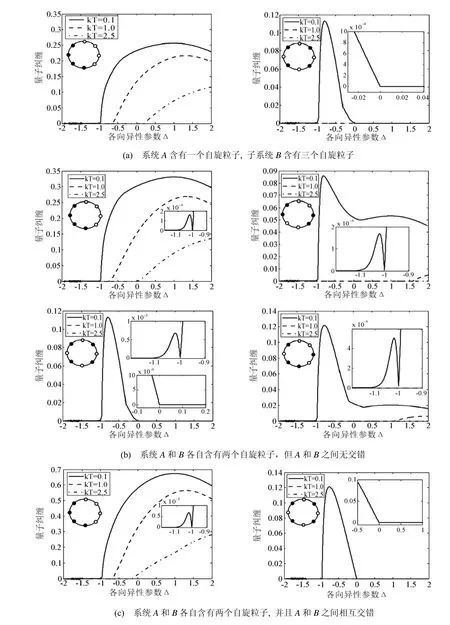
图3 不同温度下的四体量子纠缠随各向异性参数Δ的变化曲线

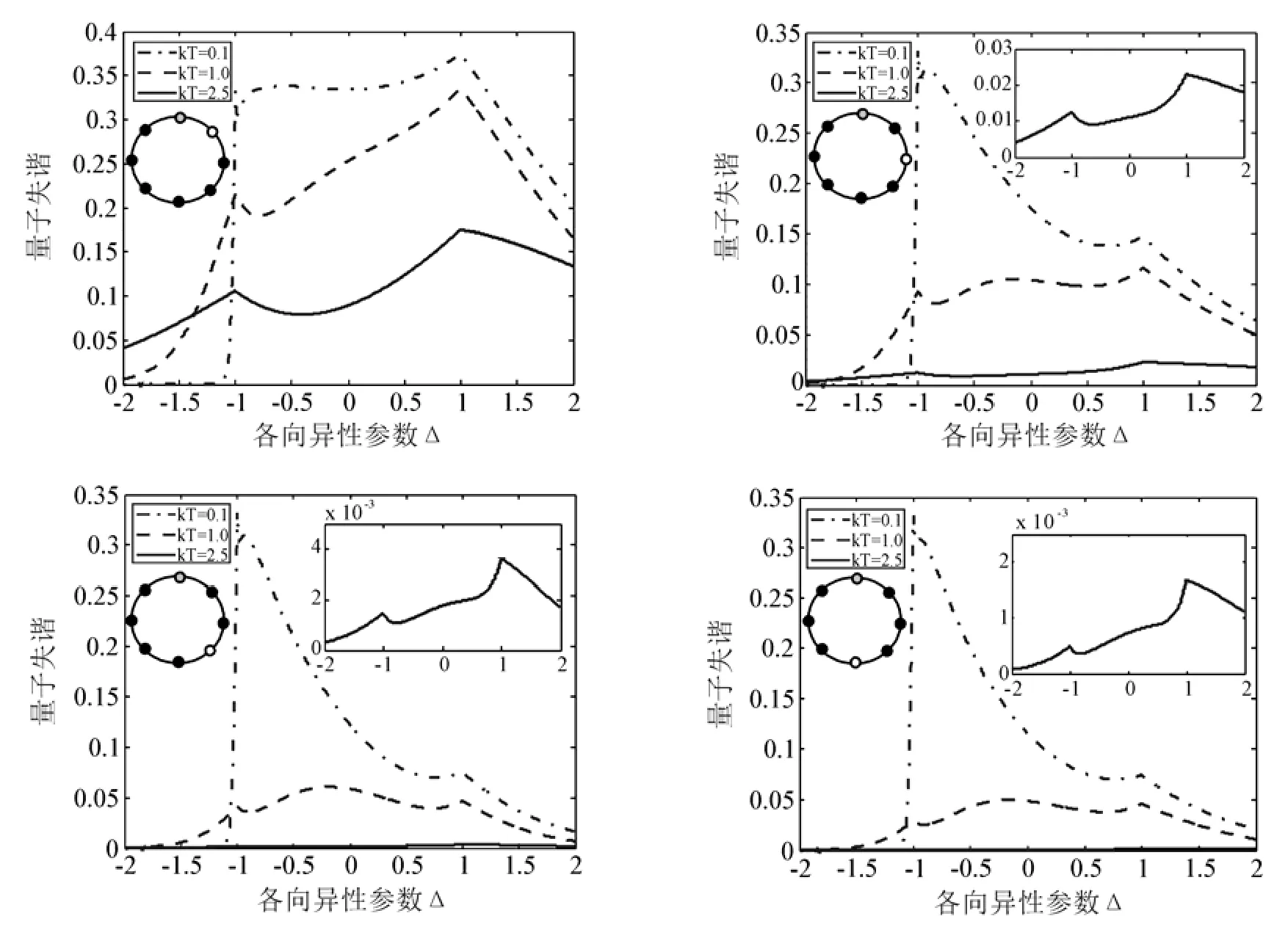
图4 不同温度下的两体量子失谐随各向异性参数Δ的变化曲线

注意到在Δ∈[-2, -1]这个区间上，A和B两粒子间没有纠缠（见图1），但在这个区间上，依然有非零的QD，显然此时QD度量的是非纠缠的量子关联，且这种非纠缠的量子关联可以随着温度的增大而增大（见图4）．

4 结论

通过研究尺度L = 8的有限温度下的XXZ环形自旋链中的量子关联，我们发现多体量子纠缠呈现出了两体所不具有的新特点．首先，多体纠缠比两体纠缠更加“强壮”；另外，在低温条件下（kT = 0.1），利用四体量子纠缠首度探测到了XXZ模型的一个相变点Δ=-1，但是Δ=1这个相变点在四体纠缠的范围内用量子纠缠却没能探测到．相比之下，TQD在探测量子相变方面更具优势，不仅利用最近邻且利用非近邻的两体TQ D也能清晰地探测到系统的相变点．因为TQD总是在量子相变的临界点处表现出尖峰行为，且在一定范围内随着温度的增大TQD依然能够保持这一特性．利用TQD的这一特性也许可以给实验上探测量子相变的临界点带来很大帮助．最后需要指出的是在我们所研究的范围内，子系统A和B之间的间隔只会消弱量子关联（纠缠、非纠缠），而温度对量子关联的影响较为复杂，温度对量子纠缠只起抑制和消弱作用，但对QD消弱和促进作用同时存在．

[1] Bennett C H, Brassard G, Crepeau C, et al. Teleporting an unknown quantum state via dual classical and Einstein-Podolsky-Rosen channels [J]. Physical Review Letters, 1993, 70：1895-1899.

[2] Bennett C H, Brassard G. Quantum cryptography：public-key distribution and coin tossing [EB/OL]. [2012-03-08].http：//www.cs.ucsb.edu/～chong/290N-W 06/BB84.pdf.

[3] Bennett C H, DiVincenzo D P. Quantum information and computation [J]. Nature, 2000, 404（6775）：247-55.

[4] Sachdev S. Quantum Phase Transitions [M]. Cambridge：Cambridge University Press, 2000：1-33.

[5] Osterloh A, Luigi A, Falci G, et al. Scaling of entanglement close to a quantum phase transition [J]. Nature, 2002, 416：608.

[6] Wootters W K. Entanglement of formation of an arbitrary state of two qubits [J]. Physical Review Letters, 1998, 80：2245-2248.

[7] O’Connor K M, Wootters W K. Entangled rings [J]. Physical Review A, 2001, 63：052302.

[8] Jin B Q, Korepin V E. Localizable entanglement in antiferromagnetic spin chains [J]. Physical Review A, 2004, 69：062314.

[9] Gu S J, Lin H Q, Li Y Q. Entanglement, quantum phase transition, and scaling in the XXZ chain [J]. Physical Review A, 2003, 68：042330.

[10] Wang X G. Entanglement in the quantum Heisenberg XY model [J]. Physical Review A, 2001, 64：012313.

[11] Wang X G, Wang Z D. Thermal entanglement in ferrimagnetic chains [J]. Physical Review A, 2006, 73：064302.

[12] Kam ta G L, Starace A F. Anisotropy and magnetic field effects on the entanglement of a two qubit Heisenberg XY chain [J]. Physical Review Letters, 2002, 88：107901.

[13] Wu L A, Sarandy M S, Lidar D A. Quantum Phase Transitions and Bipartite Entanglement [J]. Physical Review Letters, 2004, 93（25）：250404.

[14] Yang M F. Reexamination of entanglement and the quantum phase transition [J]. Physical Review A, 2005, 71（3）：030302.

[15] Jin B Q, Korepin V. Quantum S C, Toeplitz Determinants and the Fisher-Hartw ig Conjecture [J]. Journal of statistical physics, 2004, 116（1）：79-95.

[16] Keating J P, Mezzadri F. Entanglement in Quantum Spin Chains, Symmetry Classes of Random Matrices, and Conformal Field Theory [J]. Physical Review Letters, 2005, 94（5）：050501.

[17] Eisler V, Zimborás Z. Entanglement in the XX spin chain w ith an energy current [J]. Physical Review A, 2005, 71（4）：042318.

[18] Kargarian M, Jafari R, Langari A. Renormalization of entanglement in the anisotropic Heisenberg （XXZ） model [J]. Physical Review A, 2008, 77：032346.

[19] Facchi P, Florio G, Invernizzi C, et al. Entanglement of two blocks of spins in the critical Ising model [J]. Physical Review A, 2008, 78（5）：052302.

[20] Furukawa S, Pasquier V, Shiraishi J. Mutual Information and Boson Radius in a c=1 Critical System in One Dimension [J]. Physical Review Letters, 2009, 102（17）：170602.

[21] Wichterich H, Molina-Vilaplana J, Bose S. Scaling of entanglement between separated blocks in spin chains at criticality [J]. Physical Review A, 2009, 80（1）：010304.

[22] Henderson L, Vedral V. Classical, quantum and total correlations [J]. Journal of Physics A：Mathematical and General, 2001, 34：6899.

[23] Ollivier H, Zurek W H. Quantum discord：A measure of the quantumness of correlations [J]. Physical Review Letters, 2001, 88：017901.

[24] Datta A, Shaji A, Caves C M. Quantum discord and the power of one qubit [J]. Physical Review Letters, 2008, 100：050502.

[25] Lanyon B P, Barbieri M, A lmeida M P, et al. Experimental quantum computing w ithout entanglement [J]. Physical Review Letters, 2008, 101：200501.

[26] Ferraro A, Aolita L, Cavalcanti D, et al. A lmost all quantum states have nonclassical correlations [J]. Physical Review A, 2010, 81（5）：052318.

[27] Xu J S, Xu X Y, Li C F, et al.Experimental investigation of classical and quantum correlations under decoherence [J]. Nature Communication, 2010, DOI：10.1038/ncomms1005.

[28] Sarandy M S. Classical correlation and quantum discord in critical systems [J]. Physical Review A, 2009, 80（2）：022108.

[29] Chen Y X, Li S W. Quantum correlations in topological quantum phase transitions [J]. Physical Review A, 2010, 81（3）：032120.

[30] Werlang T, Trippe C, Ribeiro G A P, et al. Quantum Correlations in Spin Chains at Finite Temperatures and Quantum Phase Transitions [J]. Physical Review Letters, 2010, 105（9）：095702.

[31] Vidal G, Werner R F. Computable measure of entanglement [J]. Physical Review A, 2002, 65（3）：032314.

[32] 张永德. 量子信息物理原理[M]. 北京：科学出版社, 2005：79-91.

[33] Luo S L. Quantum discord for two-qubit systems [J]. Physical Review A, 2008, 77（4）：042303.

[34] Takahashi M. Thermodynamics of One-dimensional Solvable Models [M]. Cambridge：Cambridge University Press, 1999：46-64.

Quantum Correlations in One-dimensional Ring XXZ Spin Chain

TAN Xiaodong, GAO Wei
（School of Physics and Electronic Information Engineering, Wenzhou University, Wenzhou, China 325035）

The paper studies pair-w ise and multiple quantum entanglement and pair-w ise quantum discord in one-dimensional ring XXZ spin chain whose system scale L equals 8, and takes full account of the effects of temperature and particle interval on quantum entanglement and quantum discord in this process. The results show that three- and four-qubit entanglement are more “robust” than the pair-w ise one under the same conditions, and the critical points on which the system produces quantum phase transitions can be detected through the multiple entanglement at low temperatures. Compared w ith the quantum entanglement, the quantum discord not only can survive at higher temperatures but also always shows cusp-like behavior at the phase transition point, which endows it w ith more advantages in the detection of the phase transition point.

XXZ Spin Chain；Quantum Entanglement；Quantum Discord；Quantum Correlations；Quantum Phase Transitions

O413.1

A

1674-3563（2013）01-0036-08

10.3875/j.issn.1674-3563.2013.01.007 本文的PDF文件可以从xuebao.wzu.edu.cn获得

（编辑：王一芳）

2012-05-29

谭小东（1985- ），男，陕西宝鸡人，硕士研究生，研究方向：量子信息